数值分析:多项式的最小二乘法拟合
多项式拟合-最小二乘法
代数角度
这个方法爱看不看,看了基本也没用。
最小二乘法使用多项式拟合样本数据,其基本代数原理以下。
假设使用的是m阶多项式拟合,那么在
其误差表示为:
那么对于n个样本点,使用平方和误差量化,该误差就是数据的优化目标,自变量为各阶的权值w,有:
求E(w)极小值,需对其求偏导,为:
有:
权重系数与i无关,可以写成:
同样的,此为一个约束条件,对于m阶的多项式,存在m+1项的偏导联合约束,所以有:
写成矩阵表达式:
C++实现
如下: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
using namespace std;
using namespace cv;
//样本点集、阶数,输出拟合点
std::vector<cv::Point> PolyFit(const std::vector<cv::Point>& points, int m){
cv::Mat A = cv::Mat::zeros(m+1, m+1, CV_32FC1);
cv::Mat B = cv::Mat::zeros(m+1,1, CV_32FC1);
int n = points.size();
for(int i=0; i<m+1; i++){
for(int j=0; j<m+1; j++){
for(int k=0; k<n; k++){
A.at<float>(i, j) += std::pow(points[k].x, i+j);
}
}
}
for(int i=0; i<m+1; i++){
for(int k=0; k<n; k++)
B.at<float>(i,0) += points[k].y * std::pow(points[k].x, i);
}
cv::Mat W = cv::Mat::zeros(m+1, 1, CV_32FC1); //解出权重矩阵
if(!cv::solve(A,B,W, cv::DECOMP_LU)){
cout << "Failed To Solve" << endl;
return {};
}
//计算拟合点
vector<cv::Point> result(n, cv::Point(0,0));
for(int i=0; i<n; i++){
result[i].x = points[i].x;
for(int j=0; j<m+1; j++){
result[i].y += W.at<float>(j,0) * std::pow(points[i].x, j);
}
}
return result;
}
int main(int argc, char **argv) {
const int height = 600;
const int width = 1000;
cv::Mat canvas = cv::Mat(height, width, CV_8UC3, Scalar(255,255,255));
vector<cv::Point> points;
for(int i=0; i<width; i+=10){
int x = i;
double noise = theRNG().uniform(-30.0, 30.0);
int y = std::round((double)(height - ((double)height/width) * x) + noise);
points.emplace_back(cv::Point(x,y));
cv::circle(canvas, cv::Point(x,y), 5, Scalar(255,0,0), -1);
}
vector<cv::Point>fitPoints = PolyFit(points, 3); //三阶拟合
cv::polylines(canvas, fitPoints, false, Scalar(0,0,255), 4);
namedWindow("canvas", cv::WINDOW_NORMAL);
cv::imshow("canvas",canvas);
cout << "Done" << endl;
waitKey(0);
return 0;
}
效果: 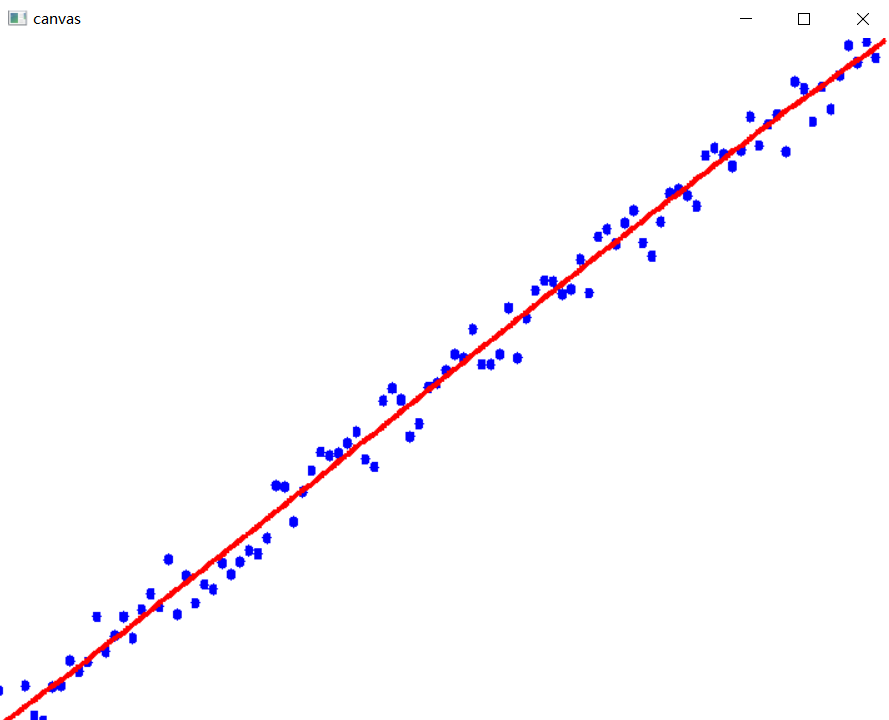
矩阵角度看待最小二乘求解
除了代数推导,从矩阵维度描述的最小二乘法有更加简便的求解方式,主要是正规方程求解以及QR分解/SVD分解等。
正规矩阵求解
假设有m阶拟合,其矩阵可以表示成:
其估计误差可以表示成一个列向量:
于是其平方误差可以表示为:
注意,此处的E已经是一个标量而非矩阵了。
对W求导:
来自前述规律,
A为对称矩阵情况下E是标量,每一项和式也应该是标量,因此其和其转置都应该相等:
所以其中两项求导均是
于是:
至此就得到了最小二乘法的正规方程:
构造该方程,求解W即可,比较简单。
C++实现
1 | ///正规方程方法 |
QR分解求解
LU分解/QR分解/SVD分解会在之后的文章详细叙述,此处仅给出结论和实现。
条件数
使用正规方程求解的一个缺陷是需要计算
这个矩阵的条件数为两亿多,具体计算可以参考Python代码:
1
2
3
4
5
6
7
8
9
10
11import numpy as np
A = np.array([[100,0.999],[100.1,1]])
cond_2 = np.linalg.cond(A,2)
cond_1 = np.linalg.cond(A,1)
cond_inf = np.linalg.cond(A, np.inf)
print(cond_2) //200220079.9225124
print(cond_1) //202301099.99296987
print(cond_inf) //202301099.99296987
这里列出条件数常见有三种条件数,分别是谱条件数(2范数条件数)、列范数(1范数条件数)和无穷范数条件数(行范数条件数):
后两种的计算比较简单,也比较常用,例如:矩阵
同理可计算其逆:
故其列条件数为21。良态(well-conditioned)矩阵的条件数应该接近1,例如接近正交的向量组成的矩阵。
所以如果使用该系数矩阵用于求解:
回到问题求解上,扩大条件数后再使用正规方程是一种风险较高的写法。所以为求稳定的数值,必须使用那些绕过直接计算
SVD分解也是可行的,其好处不仅在于其稳定性更高,而且其会计算矩阵奇异值,对于一些“非常病态”的矩阵,能够计算哪些奇异值趋近于0(意味着条件数很大),从而进行截断处理(正则化),因此也广为使用。此处简单的问题使用QR分解即可,以下。
C++实现
1 | //输入样本点集、阶数,输出拟合点 |
最小二乘与求线性变换求解区别
矩阵一种常用的应用是求两个矩阵的几何线性变换关系(仿射变换关系),其非常容易和最小二乘法混淆,不少博客认为只要是Ax = y,求解A矩阵的过程就是最小二乘法过程,这样的想法其实有失偏颇,关键还要看A是否满秩,通俗来说如果A满秩(方程数=未知数),这就是一个线性映射求解问题,如果A非满秩(方程数>未知数),才是最小误差估计问题,例如,来自OpenCV
C++记录(七):霍夫变换、仿射变换、透视变换知识可知,求解仿射变换关系至少需要三组点,求解透视变换关系至少需要四组点,例如仿射变换表示为:
如果传入三组观察点,得到的是精确解,是一个线性变换系数求解问题,所以使用普通方程求解:
如果是三组以上的观察点,那么才是需要系数估计问题,无约束条件下最小二乘法是最常用的手段,所以使用正规方程计算平方误差,或者QR分解来解原始系数方程(基本可以理解为QR方法会计算方程的平方误差):
最小二乘求旋转角度
如果矩阵只有刚性变换的特性(无坐标放缩),要求解旋转角度,那么构造的方程也会更简单。
以下代码用于估计旋转角,给出的参考点为9个,属于最小二乘求解两个矩阵(或图像)的旋转角问题,根据points和rotateMat的坐标对应关系,rotateMat的3×3矩阵恰好是points对应的矩阵旋转180°的结果,根据若干个样本点的映射关系,可以列出最小二乘的线性方程组关系,先看代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
using namespace std;
using namespace cv;
int main(int argc, char **argv) {
cv::Mat_<uchar> rawMat_x = (cv::Mat_<uchar>(3,3) <<
0, 0, 0,
1, 1, 1,
2, 2, 2
);
cv::Mat_<uchar> rawMat_y = (cv::Mat_<uchar>(3,3) <<
0, 1, 2,
0, 1, 2,
0, 1, 2
);
cv::Mat merge;
vector<cv::Mat> vp{rawMat_x, rawMat_y};
cv::merge(vp, merge);
cv::Mat points = merge.reshape(1, merge.total()); //单通道、total行,即每个xy坐标为一行,有两列
/* points:
[0, 0;
0, 1;
....
2,2]
*/
//cout << points << endl;
Mat rotateMat;
cv::flip(points, rotateMat, 0); //行颠倒
/* rotateMat:
[2, 2;
2, 1;
....
0,0]
*/
//cout << rotateMat << endl;
cv::Mat m1 = cv::Mat::ones(points.rows, 3, CV_32FC1); //初始化为1
cv::Mat(points.col(0) + points.col(1)).copyTo(m1.col(0)); //x+y
cv::Mat(points.col(0) - points.col(1)).copyTo(m1.col(1)); //x-y
cv::Mat m2 = cv::Mat::zeros(points.rows, 1, CV_32FC1);
cv::Mat(rotateMat.col(0) + rotateMat.col(1)).copyTo(m2.col(0)); //u+v
cv::Mat W;
if(!cv::solve(m1,m2, W, cv::DECOMP_QR)){ //正交QR分解求权重
cout << " can not solve! " << endl;
return -1;
}
double angle = atan2(W.at<float>(1), W.at<float>(0)); //输出系数a,b,c
if(isnan(angle)){
cout << "Nan Error" << endl;
return -1;
}
cout << "result :" << angle*180 / CV_PI << endl; //-180
cout << "Done" << endl;
waitKey(0);
return 0;
}
这里唯一值得讨论的是此处使用的线性方程组是:
为什么使用和差关系,而不是:
实际上两种方式都是等效的,只是一个地方存在差异,即:和差关系的系数比b/a恰好就是旋转角的tan函数,而后者计算出系数比例的相反数,即-b/a,是旋转角减去45度后的tan函数,即最后转换时将结果加上45度,即两种方式表示:
推导很简单,过程如下:
对于一般仿射变换(x,y)->(u,v),坐标变换公式为:
因为旋转角问题并不关心x和y方向的各自的平移量,所以重新令:
所以得旋转角与系数关系:
重新审视方程:
假设按照三角函数重新组织:
此时,得证
参考链接:

