OpenCV C++记录(十二)：齐次坐标、相机成像模型与张正友标定

齐次坐标

在视觉处理的一些数学原理中，常常看见齐次坐标的身影。所谓齐次坐标，是在原来笛卡尔坐标的基础上增加一个维度，例如二维笛卡尔坐标(x,y)对应的齐次坐标为(x,y,1)，以此类推，三维笛卡尔坐标(x,y,z)对应齐次坐标(x,y,z,1)。之所以使用齐次坐标，首先其能更方便地描述和求解几何关系，再者从2D到3D的变换，使用齐次坐标能表示一些二维空间难以表述的数学关系，例如无限远、两条平行线的交点（透视变换），其能够做到以下事情。

对点、线、平面关系的描述

点在线上、点在面上

一条二维直线的方程可以表示为： $：$ 使用向量表示其系数，为:

所以对于任意点p(x,y)，其对应齐次坐标为(x,y,1)，p在直线上的充要条件是满足二者内积为0：

同理，对于三维情况，表示空间点p(x,y,z)在平面A上：

二维线交点与共线

齐次坐标还可以方便地表达两条二维直线的交点以及确定两点所在的直线方程，结论是：

1. 两条直线的系数向量叉乘等于其交点的齐次坐标

证明：假设直线、，易知两个系数向量的叉乘得到的向量同时垂直于和，故其内积为0，结合点在线上的充要条件：

可知p既在上，也在上，故是两线的交点齐次坐标。

两个齐次坐标点的叉乘，等于两点所在直线的系数向量

假设存在直线上任一点(x,y)，其与点p1(x1,y1)和p2(x2,y2)共线必然满足方向向量相等，即：即：

另一边，计算p1(x1,y1)和p2(x2,y2)两点齐次叉乘，得：叉积结果对应Ax+by+C系数，即

可见基于方向向量和叉乘得到同一个方程，结论是成立的。

当然这个公式不能轻易推导到三维直线，因为三维的直线表示比较复杂，其有6个独立变量，例如两个平面的交线，或者一个三维向量和一个三维点来确定。

区分向量与点、无限远的表示

点和向量都可以齐次化，其中，点(x,y)齐次化成(x,y,1)，而向量齐次化为；

如果增加的维度不是单位化的1，那么前几个维度都需要乘上该系数，例如可齐次化为，特别地，齐次化为，增加的是0，那么是表示原来的坐标应该是，齐次坐标完成了对笛卡尔坐标是无限远的数学描述。

欧氏空间变换

这也是要引入齐次坐标最充分的条件。

透视变换

在二维空间中，两条平行线关系被描述成：该方程组无解，但是如果代入齐次坐标，方程成为：即：

该方程具有解(x,y,0)，如前述，该点表示的笛卡尔坐标在无穷远处，符合3D视觉中两条平行线在无穷远相交特性，因此齐次坐标在2D到3D坐标变换非常重要。

刚性变换/仿射变换

在OpenCV C++记录(七)：霍夫变换、仿射变换、透视变换我们使用了笛卡尔坐标变换来描述物体的旋转和平移，平移矩阵和旋转矩阵分别表示为：

如果使用齐次坐标，这里能将矩阵加法也简化乘左乘，为：这里的就是一种刚性变换，当旋转矩阵不再使用三角关系保证尺寸不变性，就成为了一种仿射变换矩阵。

相机标定

相机标定是用于估计相机的内参和外参，要了解内参和外参，需要了解相机成像的四个坐标系，分别是：

世界坐标系：真实世界的坐标系，例如地心坐标系、拍摄对象（标定板）、相机以及其他传感器构成的坐标系。
相机坐标系：以相机光心（透镜主光轴的中心）为原点的坐标系，相机坐标系经典取法是相机拍摄朝向为z轴，然后拿出右手，中指指向自己，大拇指水平朝右为x正方向，食指竖直向上为y轴正方向。
图像坐标系：2D坐标系，主光轴穿过的图像中心为原点，该点到相机坐标系原点的距离就是焦距f，水平为x轴，竖直为y轴。
像素坐标系：2D坐标系，即平时图像处理的坐标系，图像左上角为原点。

前三个矩阵的单位都是米，像素坐标系的单位为像素。其中世界坐标系到相机坐标系的转换由外参决定，取决于相机和拍摄对象的相对位置、运动情况等，相机坐标系到像素坐标系的转换由内参决定，取决于相机的内部参数，如成像焦距、感光尺寸、画幅尺寸（决定每个像素大小），但是因为相机的制作工艺不是完全理想的，还会受透镜本身畸变、传感器安装角度、主光轴中心与成像中心误差等影响，其中讨论透镜畸变尤其重要，畸变分成径向畸变和切向畸变，其中径向畸变由透镜本身决定（透镜边缘形状导致枕型或桶形畸变）:

径向畸变切向畸变由透镜的安装偏差引入:

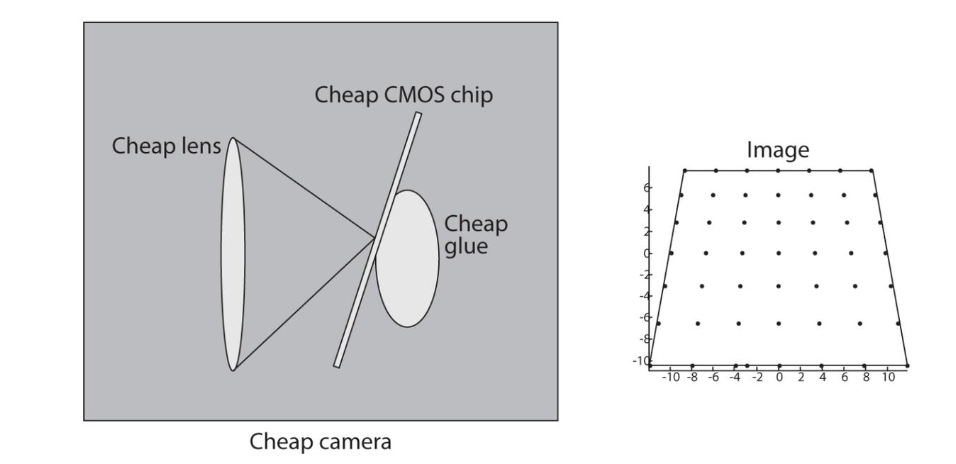
坐标系变换

标定的本质是寻找一组参数，使得已知三维坐标在图像上投影与现实投影误差最小（重投影误差最小），因此其事实上是一个拟合优化问题，注意标定是一项对误差比较敏感的工作，此处的误差一般是亚像素误差，即小数级别的像素误差。

图像坐标系(I)到像素坐标系(P)

这是最简单的情况，它们只涉及图像上的缩放和平移(米单位到像素单位)，由仿射矩阵和齐次坐标知可以表示为：即：

其中α1和α2表示单位长度(单位m)有多少个像素，β1和β2表示主光轴I原点与图像左上角P的X轴和Y轴偏移。一定注意，此处单位长度像素指的是摄像头尺寸与像素关系，例如摄像头是6mm宽，图宽1024，那么像元大小是6mm/1024pix，而不是指图片dpi（图片dpi指每英寸像素的个数，一般用于打印时长度宽度估计）。

相机坐标系(C)到图像坐标系(I)

基于相似三角形原理：

即：其中f是焦距,Zc是相机坐标系下到拍摄物体的距离。

世界坐标系(W)到相机坐标系(C)

基本的刚性变换，即旋转和平移矩阵，但注意这里不是同一个旋转平移矩阵，而是三个齐次的旋转平移矩阵，因为三维的平移旋转可以围绕X、Y、Z轴进行，代表在X、Y、Z三个方向的平移和旋转，不同于常见的绕Z轴关系，绕X、Y、Z旋转矩阵分别表示为：

因此世界坐标系与相机坐标系的转换关系为：

也可以写成齐次形式：

其中R为三个旋转矩阵相乘，t为三个方向的平移量(R|t为3×4矩阵)。求解R和t的过程也是外参求解的过程，可见有三个角度和三个偏移量共6个自由度。

总变换

综上而言，不讨论畸变情况下，将外参矩阵R|t写成统一的T，总的变换矩阵为：

除T以外的两个变换矩阵可以统一成内参矩阵，即：

标定原理/单目尺度不确定性/漂移

在坐标转换中，一个标定的难点是获取物体的三维世界准确的坐标，标定对误差偏移是极其敏感的，差之毫厘，最后效果可能失之千里。

因此最经典的张正友标定法的一个重要假设是Zw = 0，即将每张图片标定板所在的平面看成是Zw=0的面，因此从世界坐标系到像素坐标系实际上是三阶的齐次转换，涉及了八个自由度（为什么不是9个，见OpenCV C++记录(七)：霍夫变换、仿射变换、透视变换中透视变换一节），所以理论上每张图只需要四个点就能够确定该图对应的单应性矩阵，所谓单应性矩阵，包含了相机内参（不含畸变）、外参（绕Z轴平移旋转）。

如何理解标定是一个“超定”而非“正定”问题呢，对于一张照片，我们确实能够准确获取其内参和外参，其中内参是相对固定的全局参数，但是外参是随时变化的：

内参：非透镜畸变一般有五个自由度（主光轴在图像的投影中心c、像素水平和垂直焦距f、像素的非正方形性s），表示为：
外参：六自由度，三方向的平移旋转矩阵。

不同照片的对象物体距离、角度不同，因此有多少图片就可能存在多少套外参，所以这个问题只能做估计（线性拟合+非线性优化），而不能实现精确的无畸变标定。此外，因为Zw = 0的假设，标定板一定是一个平面，如果标定物体本身是一个曲面，就不应该使用张正友标定，而使用其他三维标定方法，往往复杂许多。

单目尺度不确定性/漂移

这是标定外的另一个学术问题，但也可以理解。Zw = 0的假设也造成了尺度不确定性，Zw方向应该是含有距离信息的，但是因为这个假设，导致求解的本质矩阵乘上任意的非0标量都能够使对极约束成立，表现在运动场景扩大和缩小任意倍数，都可能出现相同的图像，这被称为单目相机的尺度不确定性。

所以，单目相机无法获取对象的真实距离，例如只要你的相机足够好，在距离对象100m处也能够拍出距离对象1m的效果，要估计真实距离，只能使用三角化进行模拟，在单目相机的SLAM系统的初始化中，往往会引入初始化的平移作为单位平移（但是无法获知具体距离），也注定了该平移是存在和实际的距离误差的，该误差会随着运动累积，导致建图形状失真等等，所以在许多场景下需要引入回环检测来进行闭环的修正。另外一些方法是使用双目相机，因为双目距离是固定的，其三角化视角的误差也是固定的，或者其他融合测距雷达的方案。

相机畸变

求解内参中需要解决的问题是透镜引起的畸变问题，分成透镜本身形状导致的径向畸变以及透镜安装不平行带来的切向畸变。

径向畸变分成桶形和枕形畸变，这是由k系数的符号决定，且随着离中心的距离变大而增大，一般根据二次或高次多项式纠正：

和表示畸变坐标，x、y表示畸变矫正后坐标，r是离图像中心距离；一般只有鱼眼摄像头才会使用k3及以上来消除径向畸变。

切向畸变的多项式纠正：

故总的纠正公式为上述式子相加，畸变系数考虑顺序优先级为k1、k2、p1、p2、k3...

为图像添加畸变

鉴于目前基本所有的手机相机算法都会预先去除镜头畸变，要想做相关实验可能只有一些嵌入式摄像头才可能做到，这里提供一种人为批量对图片创造桶形或枕型畸变的方法：

void addDistortion(cv::Mat& srcMat, cv::Mat& result, double distortion){
    result = Mat::zeros(srcMat.rows, srcMat.cols, CV_8UC1);
    //畸变会超出原有图片展示范围，先做50个填充
    int padSize = 50;
    copyMakeBorder(srcMat,srcMat,padSize,padSize,padSize,padSize,cv::BORDER_CONSTANT, Scalar(0));

    ////坐标转换参数
    double px = srcMat.cols/0.8;
    double py = srcMat.rows/0.8;
    double cx = srcMat.cols/2 - 100;
    double cy = srcMat.rows/2 - 50 ; 

    double scale_x = (double)srcMat.cols/(double)result.cols;
    double scale_y = (double)srcMat.rows/(double)result.rows;

    for(int i=0; i<result.rows; i++){
        double y = (double)(i - cy)/py ; //py为比例系数，值为焦距f/(像距Zc * 像元大小dy) 
        for(int j=0; j<result.cols; j++){
            //相机坐标系
            double x = (double)(j - cx)/px ; //px为比例系数，值为焦距f/(像距Zc * 像元大小dx) 

            double r = x * x + y * y;

            //相机坐标系下添加畸变
            double new_x = (1 + distortion* r)*x;
            double new_y = (1 + distortion* r)*y;

            //计算畸变的图像坐标
            new_x = new_x * px + cx;
            new_y = new_y * py + cy;

            //双线性插值
            double y_ = (new_y + 0.5)*scale_y + 49.5;
            double x_ = (new_x + 0.5)*scale_x + 49.5;

            int x1 = round(x_+0.5) - 1;
            int x2 = x1 + 1;
            int y1 = round(y_+0.5) - 1;
            int y2 = y1 + 1;

            //桶形往内缩，枕型往外扩，排除越界情况
            if(x1<0 || y1 < 0 || x2 >= srcMat.cols || y2 >= srcMat.rows){
                continue;
            }

            double w1 = (y2-y_)*(x2-x_);   //权值计算
            double w2 = (y2-y_)*(x_-x1);
            double w3 = (y_-y1)*(x2-x_);
            double w4 = (y_-y1)*(x_-x1);
            //cout << x1 << " " << x2 << " " << y1 << " " << y2 << endl; 

            result.at<uchar>(i,j) = w1*srcMat.at<uchar>(y1,x1) + w2*srcMat.at<uchar>(y1,x2) + \
            w3*srcMat.at<uchar>(y2,x1) + w4*srcMat.at<uchar>(y2,x2);
        }
    }
}

分别是1.6和-0.6系数的畸变效果：

张正友标定

正如前文所述，张正友标定是一种2D标定方法，只需要一块标定板即可相机标定，可以从此处获得，算法会自动检测棋盘格中的内角点，并且将内角点精细化成亚像素坐标，随即根据图片估算相机的内参矩阵的外参旋转平移矩阵，根据内外参矩阵生成X和Y方向的映射矩阵表，最后对图片进行remap即可去除畸变。

OpenCV实现

以下是一个完整示例，对刚刚加入人工畸变的图片进行校准：

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

void addDistortion(cv::Mat& srcMat, cv::Mat& result, double distortion){
    result = Mat::zeros(srcMat.rows, srcMat.cols, CV_8UC1);
    int padSize = 50;
    copyMakeBorder(srcMat,srcMat,padSize,padSize,padSize,padSize,cv::BORDER_CONSTANT, Scalar(0));

    ////像素-图像坐标转换参数，px是假设的像元大小比例，cx是坐标偏移
    double px = srcMat.cols/0.8;
    double py = srcMat.rows/0.8;
    double cx = srcMat.cols/2 - 100;
    double cy = srcMat.rows/2 - 50 ; 

    double scale_x = (double)srcMat.cols/(double)result.cols;
    double scale_y = (double)srcMat.rows/(double)result.rows;

    for(int i=0; i<result.rows; i++){
        //相机坐标系
        double y = (double)(i - cy)/py ; //py为比例系数，值为焦距f/(像距Zc * 像元大小dy) 

        for(int j=0; j<result.cols; j++){
            //相机坐标系
            double x = (double)(j - cx)/px ; //px为比例系数，值为焦距f/(像距Zc * 像元大小dx) 

            double r = x * x + y * y;

            //相机坐标系下添加畸变
            double new_x = (1 + distortion* r)*x;
            double new_y = (1 + distortion* r)*y;

            //计算畸变的图像坐标
            new_x = new_x * px + cx;
            new_y = new_y * py + cy;

            //双线性插值
            double y_ = (new_y + 0.5)*scale_y + 49.5;
            double x_ = (new_x + 0.5)*scale_x + 49.5;

            int x1 = round(x_+0.5) - 1;
            int x2 = x1 + 1;
            int y1 = round(y_+0.5) - 1;
            int y2 = y1 + 1;

            //桶形往内缩，枕型往外扩，排除越界情况
            if(x1<0 || y1 < 0 || x2 >= srcMat.cols || y2 >= srcMat.rows){
                continue;
            }

            double w1 = (y2-y_)*(x2-x_); //权值计算
            double w2 = (y2-y_)*(x_-x1);
            double w3 = (y_-y1)*(x2-x_);
            double w4 = (y_-y1)*(x_-x1);

            result.at<uchar>(i,j) = w1*srcMat.at<uchar>(y1,x1) + w2*srcMat.at<uchar>(y1,x2) + \
            w3*srcMat.at<uchar>(y2,x1) + w4*srcMat.at<uchar>(y2,x2);
        }
    }
}


int main(){

    const int chessWidth = 9;
    const int chessHeight = 6;
    std::vector<cv::Point3f> worldPoints;

    for(int i = 0; i < chessHeight; i++){
        for(int j=0; j<chessWidth; j++){
            worldPoints.push_back(cv::Point3f(j, i, 0));
        }
    }

    int cnt = 1;

    std::vector<std::vector<cv::Point3f>> objPoints; //对象点
    std::vector<cv::Point2f> imgPoint; //图像点
    std::vector<std::vector<cv::Point2f>> imgPoints;

    while(cnt <= 13){  //循环读入标定图片，宜10-20张
        std::string path = ("D:/Documents/Desktop/calibPic/" + std::to_string(cnt) + ".png");
        std::string output1Path = ("D:/Documents/Desktop/calibPic/" + std::to_string(cnt) + "_dis.png"); //畸变图
        std::string output2Path = ("D:/Documents/Desktop/calibPic/" + std::to_string(cnt) + "_calib.png"); //标定图
        std::string output3Path = ("D:/Documents/Desktop/calibPic/" + std::to_string(cnt) + "_res.png"); //纠正畸变图
        cv::Mat input = cv::imread(path,0);

        cv::Mat distortionMat = input.clone();
        addDistortion(input, distortionMat, 1.6);   //添加桶形畸变
        cv::imwrite(output1Path, distortionMat);

        //-----------------------对畸变图进行标定---------------------------------------
        ///检测二维图像点
        ///自适应阈值、归一化亮度和对比度（提高检测鲁棒性）、快速检测
        bool found = cv::findChessboardCorners(distortionMat, cv::Size(chessWidth, chessHeight), imgPoint, cv::CALIB_CB_ADAPTIVE_THRESH | cv::CALIB_CB_NORMALIZE_IMAGE | cv::CALIB_CB_FAST_CHECK);
        if(found){
            //亚像素化
            cv::TermCriteria criteria(TermCriteria::EPS | TermCriteria::Type::MAX_ITER, 30, 0.001);
            cv::cornerSubPix(distortionMat, imgPoint, cv::Size(5, 5), cv::Size(-1, -1), criteria);

            // 在棋盘上显示检测到的角点
            cv::Mat calibShow;
            cv::cvtColor(distortionMat, calibShow, cv::COLOR_GRAY2BGR);
            cv::drawChessboardCorners(calibShow, cv::Size(chessWidth, chessHeight), imgPoint, found);

            objPoints.push_back(worldPoints);
            imgPoints.push_back(imgPoint);
            cv::imwrite(output2Path, calibShow);
        }

        cv::Mat cameraMatrix,distCoeffs, R, T; //相机内参、透镜畸变、旋转平移外参
        cv::calibrateCamera(objPoints, imgPoints, distortionMat.size(), cameraMatrix, distCoeffs, R, T);
        cv::Mat mapx,mapy;
        initUndistortRectifyMap(cameraMatrix, distCoeffs, cv::Mat(), cameraMatrix, distortionMat.size(), CV_16SC2, mapx, mapy);
        cv::Mat result;
        remap(distortionMat,result,mapx, mapy, INTER_LINEAR);
        cv::imwrite(output3Path, result);

        cnt++;
    }

    cout << "done" <<endl;
    waitKey(0);
    return 0;
}

此处的标定图是使用第三个参考链接的示例图，存在像素不清的情况，如果有条件使用硬纸板或者玻璃板素材，应该会更好，以下:

检测和绘制角点：标定效果：畸变前（左）、校准后（右）

参考链接：