龙格现象(Runge Phenomenon)

在对数据进行估计时往往有拟合和插值两种方法，拟合只会尽量估计数据集的整体分布趋势，不会确保经过所有的样本点，而插值会经过所有的样本点，但一般而言线性插值产生折线效果，其一阶导数不连续，往往使用高阶插值，但高阶插值可能产生龙格现象，龙格现象指的是均匀分布的插值点函数阶数升高，在多项式端点处可能造成振荡，产生严重误差，龙格现象的原因剖析详见龙格现象，解决这种现象可以通过引入高斯或切比雪夫插值点，或者使用分段的插值进行解决。

三次样条插值(Cubic Spline Interpolation)

样条插值源自工程制图，其通过固定的钉子，将柔软的木条固定: 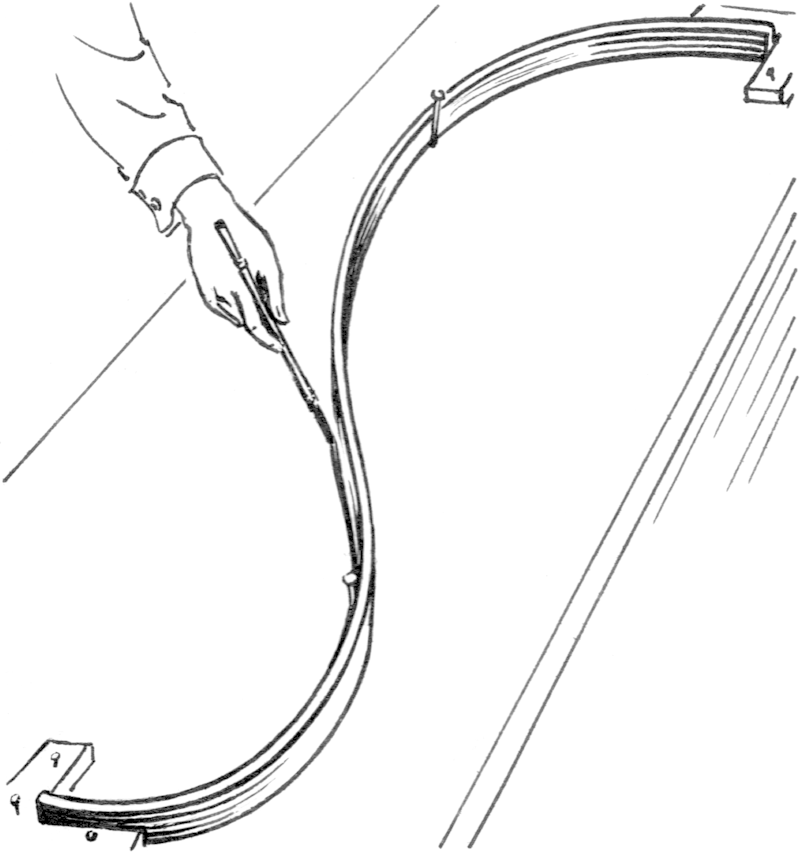工程制图

引入数学，木条的函数可以由分段的端点函数进行表示，保证了整体函数的光滑性，三次样条插值在数学上是一个三次分段函数：

可见其有4n个方程参数，但只能建立4n-2个方程.

具体而言，根据函数连续性，n+1个端点，可建立2n个方程(两侧端点只能各建立一个方程)：

因为函数光滑，其除两侧外的端点满足二阶导数连续、一阶导数连续，分别建立n-1个方程：

剩下两个条件根据边界假设确定，不同的边界条件对应的插值效果也不同，延申了若干种插值方法，如自然样条插值、非扭结样条插值、周期样条插值和固定端点样条插值，因为自然样条插值可以对未知边界特性的数据进行预测，比较常用，此处也仅给出其详细推导和实现。

自然样条插值(Natural Spline)

自然样条插值的假设是两侧端点的二阶导数为0，即：

计算方法

自然样条插值计算关键在于构造二阶导S''(x)和S(x)的关系，在一个输入系统中和是确定的，其增量Δx也是确定的，根据推导可以构造出以上关系，结论如下:

其中，代表邻近样本点的x坐标差，，代表函数在的二阶导值，使用该原理根据样本点可先推算出系数，该系数可进一步算出所有的系数，从而进行三次样条自然插值。

该结论的推导过程如下：

对于区间内的任一点方程，S(x)函数是处处连续的，这个区间可理解成包含端点(即可能分属于两个解析式)，也可以理解成不包含端点（有同一个解析式），可写成：

令，得到函数、函数一阶导和二阶导与系数关系：

因为样本自然插值的边界条件是两侧端点二阶导数为0，因此需要查找二阶导和系数关系，方便起见设，根据上式知b系数关系：

此处一个巧妙的方式根据（点的函数连续性）和 （点的二阶导数连续性），得：

此处令，得：

故有：

最后一块拼图来自一阶导的连续性：仍然令：

代入、、，化简得：

且根据边界条件、，写成矩阵形式即为上述结论所示。

C++实现

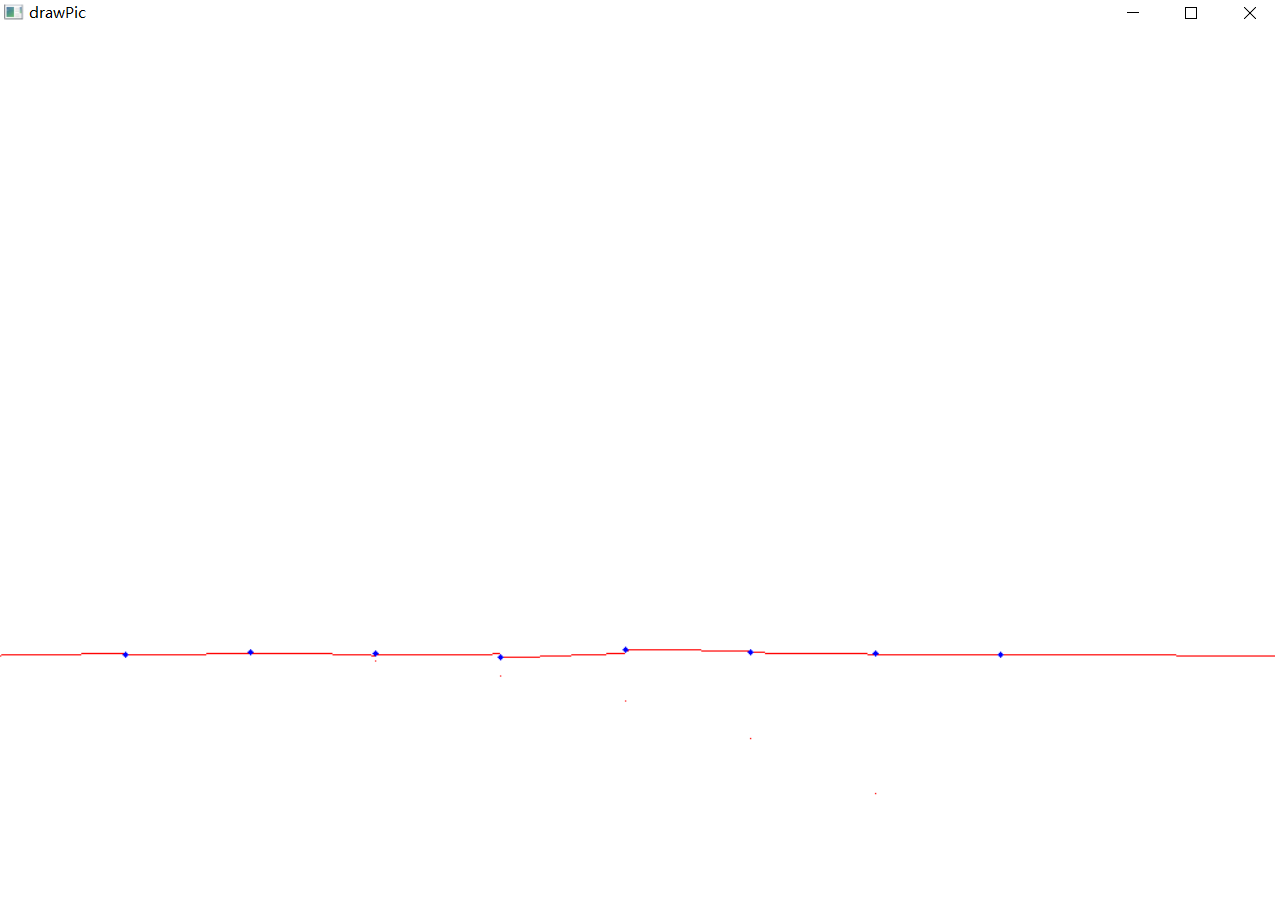
示例：使用三次自然样条插值对8个样本点插值成1024个点： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
#include <opencv2/opencv.hpp>
#include <iostream>

using namespace std;
using namespace cv;

void splineNatural(const vector<cv::Point2f>& points, cv::Mat& params){
    const size_t n = points.size();

    if(n < 3){ //自然样条插值至少需要三个点做推导
        cout << "Invalid Interpolation" << endl; 
        return;
    }

    vector<float> dx(n-1, 0);
    vector<float> dy(n-1, 0);

    //构造h = Δx矩阵，以及Δy矩阵
    for(int i=0; i<=n-2; i++){
        dx.at(i) = points.at(i+1).x - points.at(i).x;
        dy.at(i) = points.at(i+1).y - points.at(i).y;
    }

    cv::Mat H = cv::Mat::zeros(n, n, CV_32FC1);
    H.at<float>(0,0) = 1;
    H.at<float>(n-1, n-1) = 1;

    cv::Mat Y = cv::Mat::zeros(n, 1, CV_32FC1);
    Y.at<float>(0,0) = 0;
    Y.at<float>(n-1,0) = 0;

    for(int i = 1; i <= n-2; i++){
        ///h矩阵构造n×n系数矩阵H
        H.at<float>(i, i-1) = dx.at(i-1);
        H.at<float>(i, i) = 2*(dx.at(i-1) + dx.at(i));
        H.at<float>(i,i+1) = dx.at(i);

        //等号右侧矩阵
        Y.at<float>(i,0) = 6*(dy.at(i)/dx.at(i) - dy.at(i-1)/dx.at(i-1));
    }

    cout << "pppp" <<H << endl;

    //求解m矩阵
    cv::Mat M;
    M = H.inv()*Y;

    cout << "xcasa" <<M << endl;

    vector<float> a(n-1, 0); //三次项系数
    vector<float> b(n-1, 0); 
    vector<float> c(n-1, 0);
    vector<float> d(n-1, 0); //常数项

    //根据ai、bi、ci、di与m关系获得系数矩阵
    //n个点能建立n-1个方程，含4n-4个未知数，下表对应0到n-2
    for(int i = 0; i<=n-2; i++){
        a.at(i) = (M.at<float>(i+1) - M.at<float>(i)) / (6*dx.at(i));
        b.at(i) = (M.at<float>(i))/2;
        c.at(i) = dy.at(i)/dx.at(i) - M.at<float>(i)*dx.at(i)/3 - M.at<float>(i+1)/6;
        d.at(i) = points.at(i).y;
    }

    cv::Mat A(a),B(b), C(c), D(d);
    std::vector<cv::Mat> mergeVp{A,B,C,D};
    cv::hconcat(mergeVp, params);
}

///模拟标定点
void doSpline(vector<cv::Point2f>& calibPoint, cv::Mat& drawPic){
    cv::Mat paramsMat;
    splineNatural(calibPoint,paramsMat); //获取参数矩阵

    for(int x=0; x < 1024; x++){ //假设插值需要1024个点
        int paramIdx = 0;
        int calib_x = 0;
        for(int num = 0; num <= calibPoint.size() - 2; num ++){
            if(x > calibPoint[num].x && x < calibPoint[num+1].x){ 
                paramIdx = num;
                calib_x = calibPoint[num].x;
                break;
            }
            else if(x >= calibPoint.back().x){
                paramIdx = calibPoint.size()-2;
                calib_x = calibPoint.back().x;
                break;
            }
        }

        float a = paramsMat.at<float>(paramIdx,0);
        float b = paramsMat.at<float>(paramIdx,1);
        float c = paramsMat.at<float>(paramIdx,2);
        float d = paramsMat.at<float>(paramIdx,3);

        float y = std::round(a*(x-calib_x)*(x-calib_x)*(x-calib_x) + b*(x-calib_x)*(x-calib_x) + c*(x-calib_x) + d);

        if(y<0 || y>=drawPic.rows || x<0 || x>=drawPic.cols){
            cout << "xxx" << y <<" "<< x <<endl;
            continue;
        }
        drawPic.at<Vec3b>(y, x) = Vec3b(0,0,255);
    }
    for(const auto& pos : calibPoint){
        circle(drawPic, Point(pos.x, pos.y), 2, Scalar(255,0,0), -1);
        drawPic.at<Vec3b>(pos.y, pos.x) = Vec3b(255, 0, 0);
    }
}

int main(){
    cv::Mat drawPic(1024,1024,CV_8UC3); //底图
    drawPic.setTo(255);
    std::vector<Point2f> calibPoint;
    calibPoint.push_back(cv::Point2f(100,500.5)); 
    calibPoint.push_back(cv::Point2f(200,498.8));
    calibPoint.push_back(cv::Point2f(300,499.6));
    calibPoint.push_back(cv::Point2f(400,502.1));
    calibPoint.push_back(cv::Point2f(500,496.6));
    calibPoint.push_back(cv::Point2f(600,498.2));
    calibPoint.push_back(cv::Point2f(700,499.5));
    calibPoint.push_back(cv::Point2f(800,500.2));
    doSpline(calibPoint, drawPic);

    cv::imshow("drawPic",drawPic);

    cout <<"done" << endl;
    cv::waitKey(0);
    cv::destroyAllWindows();
    return 0;
}
效果如下： 插值效果

非扭结样条插值(Not-a-knot Spline)

非扭结样条插值的假设是第一段和第二段、第n-1段和第n端函数的三阶导数也相等，即： 故有、；

周期样条插值(Periodic Spline)

周期样条插值假设两侧端点的一阶导数和二阶导数相等，这个假设尤其适用于周期函数，即:

固定端点样条(Clamped Spline)

固定端点样条的假设是第一段函数和第n段函数的三次项系数为0，即:

参考链接：

  1. 龙格现象

  2. 样条插值(Spline Interpolation)

  3. 三次样条（cubic spline）插值