OpenCV C++记录(十一)：Mat数据规范化、灰度直方图与均衡算法

归一化

讨论归一化主要是图像数据分析中用到，cv::normalize支持将Mat数据归一化:

void normalize(
    cv::InputArray src,
    cv::InputOutputArray dst,
    double alpha = (1.0),    //归一化倍数/下限，根据类型不同而不同；
    double beta = (0.0),     //无意义或归一化上限，根据类型不同而不同，见下文；
    int norm_type = 4, //默认L2范数，四种方式，cv::NORM_L1/cv::NORM_L2/cv::NORM_INF/cv::NORM_MINMAX
    int dtype = -1,    //输出矩阵类型，-1保持和原矩阵一致
    cv::InputArray mask = noArray()   //位置掩图，如果对src某区域归一化传入同size的mask(对应roi置白)
)

这里重要的地方是norm_type对应几种规范化类型，分别是L1范数(平均值)、L2范数、最大值以及范围规范化。

cv::NORM_L1/cv::NORM_L2/cv::NORM_INF

这几个类型的共同点是无需beta参数，alpha定义了归一化的倍数,计算方法比较简单:

L1范数：每个元素除以所有元素平均值，乘alpha即为归一化数；
L2范数：每个元素除以(所有元素的平方和的开方)，乘alpha即为归一化数；
NORM_INF：每个元素除以最大值元素，乘alpha即为归一化数

示例：

cv::Mat input = (cv::Mat_<uchar>(5,1)<<     
    1,2,3,4,5 
); 

cv::Mat output1,output2,output3;
//此处beta参数0无用
cv::normalize(input, output1, 1, 0 ,cv::NORM_L1, CV_32FC1); ///0.0666667 0.133333 0.2 0.266667 0.333333 
cv::normalize(input, output2, 1, 0 ,cv::NORM_L2, CV_32FC1); ///0.13484 0.26968 0.40452 0.53936 0.6742 
cv::normalize(input, output3, 1, 0 ,cv::NORM_INF, CV_32FC1); ///0.2 0.4 0.6 0.8 1

cv::NORM_MINMAX

对于该类型，alpha定义了范围起点，beta定义了范围终点，input所有数据都会被线性地映射到[alpha,beta]上：

cv::Mat input = (cv::Mat_<uchar>(5,1)<<
    1,2,3,4,5 
); 
cv::normalize(input, output4, 0, 255 ,cv::NORM_MINMAX,CV_32FC1); ///1 64.5 128 191.5 255 
cv::normalize(input, output5, 255, 0 ,cv::NORM_MINMAX,CV_32FC1); ///1 64.5 128 191.5 255，反转也可以？？

灰度直方图

灰度直方图是图像分析的常见参考对象，其函数原型为：

void cv::calcHist(
    const std::vector<cv::Mat>& images,  //输入图像数组
    const std::vector<int>& channels,    //要统计的输入图像通道
    const cv::InputArray mask,           //统计区域掩图ROI，若统计全图传cv::Mat
    cv::OutputArray hist,                //输出直方图，为CV_32F类型，返回每个像素的个数
    const std::vector<int>& histSize,    //灰度桶大小，如256即单独统计每个灰度的像素个数
    const std::vector<float>& ranges,    //统计灰度范围
    bool accumulate = false              //hist是否随着Mat数组累加，为false会清空
);

这里面最重要的是返回数据hist，代表了每种像素的个数，个数之所以是浮点类型，主要是为了向后兼容，因为基于直方图的算法还有很多，避免再进行类型转换。

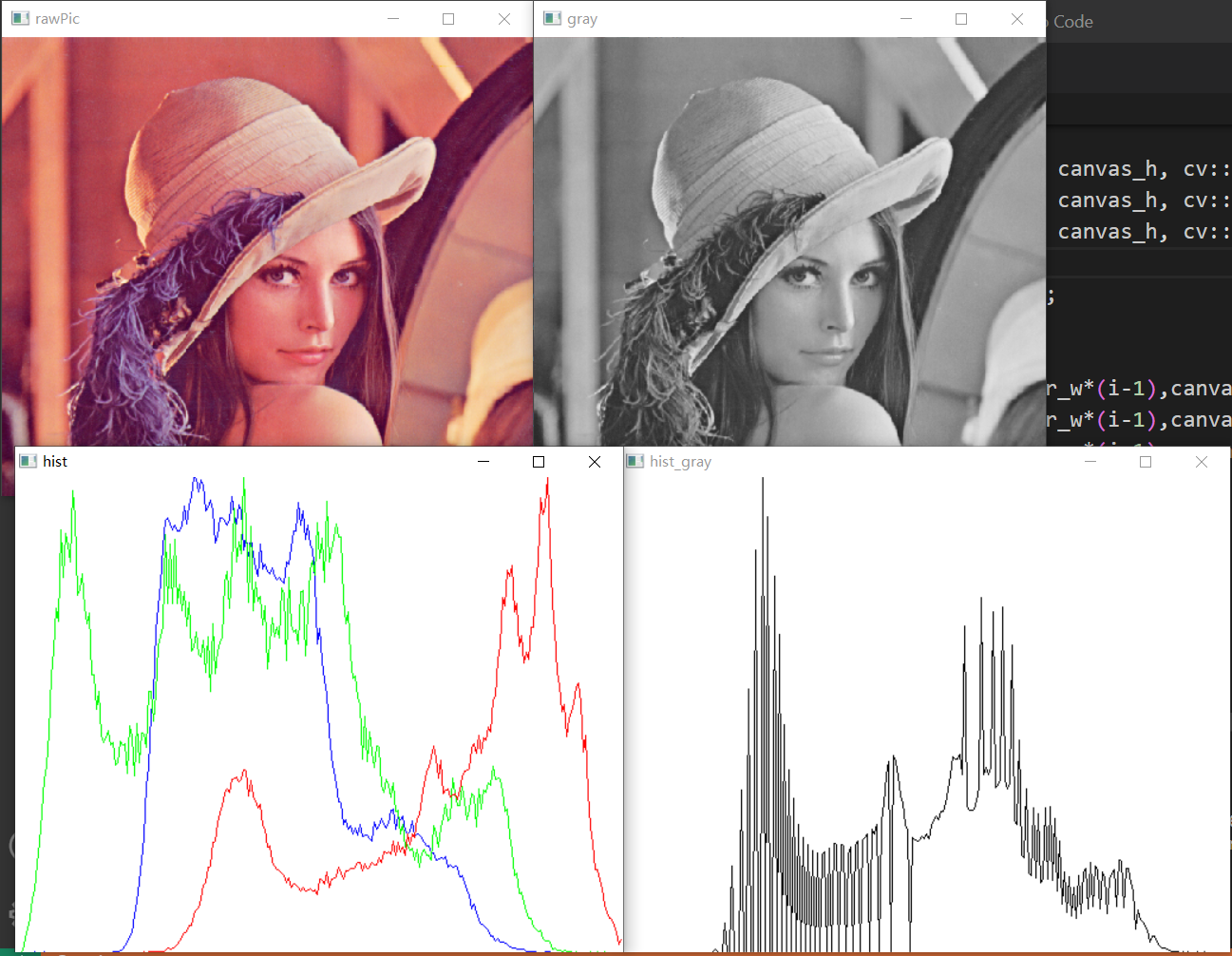
绘制简单的灰度直方图(其实这里是折线图；此处，对于彩图，如果处理channels是{0,1,2}，那么返回的hist将是一个三维Mat对象，其算法复杂度就达到了,而且三维Mat的遍历也比较麻烦，因此应该先分离颜色通道独立处理效果更佳：

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

int main(){
    int binSize = 256;
    //灰图
    Mat rawPic_gray = imread("D:/Documents/Desktop/note/jLena10.jpeg",0);
    cv::Mat hist_gray;
    cv::calcHist(vector<cv::Mat>{rawPic_gray}, vector<int>{0}, cv::Mat(), hist_gray, vector<int>{binSize}, vector<float>{0,256});
    //单通道计算直方图，输出dims是一维单通道的
    cout<<hist_gray.dims<<endl; //但输出2，因为Mat将一维看成n*1;

    int canvas_w = 512;
    int canvas_h = 400;
    int pillar_w = canvas_w/binSize;

    cv::Mat canvas(canvas_h,canvas_w,CV_8UC3);
    canvas.setTo(255);

    //将hist返回各像素范围映射到纵坐标
    cv::normalize(hist_gray, hist_gray, 0, canvas_h, cv::NORM_MINMAX);
    //折线图
    for(int i=1; i<binSize; i++){
        cv::line(canvas,Point(pillar_w*(i-1),canvas_h - hist_gray.at<float>(i-1)), \
                 Point(pillar_w*(i),canvas_h-hist_gray.at<float>(i)),Scalar(0));
    }
    cv::imshow("hist_gray",canvas);

    //BGR彩图
    Mat rawPic = imread("D:/Documents/Desktop/note/jLena10.jpeg",1);

    vector<cv::Mat> split;
    cv::Mat hist_b,hist_g,hist_r;
    cv::split(rawPic,split);
    cv::calcHist(vector<cv::Mat>{split[0]}, vector<int>{0}, cv::Mat(), hist_b, vector<int>{binSize}, vector<float>{0,256});
    cv::calcHist(vector<cv::Mat>{split[1]}, vector<int>{0}, cv::Mat(), hist_g, vector<int>{binSize}, vector<float>{0,256});
    cv::calcHist(vector<cv::Mat>{split[2]}, vector<int>{0}, cv::Mat(), hist_r, vector<int>{binSize}, vector<float>{0,256});

    cv::normalize(hist_b, hist_b, 0, canvas_h, cv::NORM_MINMAX);
    cv::normalize(hist_g, hist_g, 0, canvas_h, cv::NORM_MINMAX);
    cv::normalize(hist_r, hist_r, 0, canvas_h, cv::NORM_MINMAX);

    cv::Mat canvas2 = canvas.clone();
    canvas2.setTo(255);
    for(int i=1; i<binSize; i++){
        cv::line(canvas2,Point(pillar_w*(i-1),canvas_h - hist_b.at<float>(i-1)),Point(pillar_w*(i),canvas_h-hist_b.at<float>(i)),Scalar(255,0,0));
        cv::line(canvas2,Point(pillar_w*(i-1),canvas_h - hist_g.at<float>(i-1)),Point(pillar_w*(i),canvas_h-hist_g.at<float>(i)),Scalar(0,255,0));
        cv::line(canvas2,Point(pillar_w*(i-1),canvas_h - hist_r.at<float>(i-1)),Point(pillar_w*(i),canvas_h-hist_r.at<float>(i)),Scalar(0,0,255));
    }
    cv::imshow("hist",canvas2);

    cout<<"Done"<<endl;
    waitKey(0);
    cv::destroyAllWindows();
    return 0;
}

效果图：

直方图均衡化（Histogram Equalization，HE）

灰度均衡化是大多数图像的优化选择方法，一般如果灰图直方图过多的像素集中在某一区域，图像会表现得过亮或者过暗，而图像质量好的图像(亮度适中、对比度高)，往往具有较为均匀的灰度分布。

均衡化的工具是累计分布函数(Cumulative Distribution Function,CDF)，即分布函数，有概率论基础的应该知道它是概率密度函数(Probability Density Function,PDF)的积分，对于CDF的F(x)，它的通俗定义是x落在(-∞,x)的概率，例如对于256灰度级，概率只可能在0-255，故F(-1) = 0,F(255) = 1；

均衡化的数学原理

可能仅知道分布函数原理也很难理解，为什么分布函数能够将图像灰度进行“均衡化”效果，下面是关于概率论的数学推导，无兴趣或相关基础的可以跳过。

基于CDF的变换，假设从像素r到像素s的变换关系：

其中p(r)是原像素的概率密度函数，目前我们假设其为一个连续函数，得到的积分就是对应的分布函数；

要表示目标图像均衡化，只需证明s的概率密度是一个常数，这里我们仅讨论转换关系，所以s和r本身可以看成0到1区间的归一化的、连续的像素，即证：即可。

因为T(r)函数是一个分布函数，其非递减、处处连续(无间断点)，利用一个结论:

此处假设，那么有，即h(Y)为g(X)的反函数。

故无需通过分布函数计算即可获得其概率密度关系：

对于此处，根据连续函数的积分求导：代入有

故当灰度级为连续时(灰度数量级无限)，使用了分布函数进行均衡化的图像像素在灰度上的分布符合均匀分布。

对于离散灰度，均衡化步骤是：

计算每个灰度级的CDF：其中是当前灰度级，是灰度级总数，是每个灰度级的像素个数，是总像素个数；
乘上，就是当前灰度级k被映射到的新像素值。

例如，灰度为0的像素比例是0.2，灰度为1的比例是0.1，那么灰度0位置对应的像素应该是0.2×255 = 51灰度，灰度1位置像素应该是(0.2+0.1)×255 = 76.5(取76灰度)，以此类推。

均衡化应用

CV提供了直接均衡化的函数：

1	void equalizeHist(cv::InputArray src, cv::OutputArray dst)

参数比较简单，这里要注意的是对多通道图（彩色图）的均衡化：因为一个像素的BGR比例是不对等的，如果将通道分离各自均衡化后再合并，则改变了原来像素的BGR比例，导致图像失真。

正确的均匀化方法是将彩图转到HSV空间下，对其明度(Value)进行均衡化（明度控制黑白）：

这个代码能够帮助你比较均衡化前后的灰度数据：

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

int main(){
    //BGR彩图
    Mat rawPic = imread("D:/Documents/Desktop/note/jLena10.jpeg",1);

    auto calcHistAndDraw = [](cv::Mat& rawPic, string canvas_name){
        int binSize = 256;

        //绘图画布宽高、每个灰度宽度
        int canvas_w = 512; 
        int canvas_h = 400;
        int pillar_w = canvas_w/binSize;

        cv::Mat canvas(canvas_h,canvas_w,CV_8UC3);
        canvas.setTo(255);

        if(rawPic.channels() == 1){
            cv::Mat hist_gray;
            cv::calcHist(vector<cv::Mat>{rawPic}, vector<int>{0}, cv::Mat(), hist_gray, vector<int>{binSize}, vector<float>{0,256},false);
            //单通道计算直方图，输出dims是一维单通道的
            cout<<hist_gray.dims<<endl; //但输出2，因为Mat将一维看成n*1;


            //将hist返回各像素范围映射到纵坐标
            cv::normalize(hist_gray, hist_gray, 0, canvas_h, cv::NORM_MINMAX);
            //折线图
            for(int i=1; i<binSize; i++){
                cv::line(canvas,Point(pillar_w*(i-1),canvas_h - hist_gray.at<float>(i-1)),Point(pillar_w*(i),canvas_h-hist_gray.at<float>(i)),Scalar(0));
            }
            cv::imshow(canvas_name,canvas);
        }

        else if(rawPic.channels() == 3){ //三通道
            vector<cv::Mat> split;
            cv::Mat hist_b,hist_g,hist_r;
            //三通道分离
            cv::split(rawPic,split);
            //获取每个通道的灰度直方图
            cv::calcHist(vector<cv::Mat>{split[0]}, vector<int>{0}, cv::Mat(), hist_b, vector<int>{binSize}, vector<float>{0,256});
            cv::calcHist(vector<cv::Mat>{split[1]}, vector<int>{0}, cv::Mat(), hist_g, vector<int>{binSize}, vector<float>{0,256});
            cv::calcHist(vector<cv::Mat>{split[2]}, vector<int>{0}, cv::Mat(), hist_r, vector<int>{binSize}, vector<float>{0,256});

            //将灰度直方图个数规范化到纵坐标范围
            cv::normalize(hist_b, hist_b, 0, canvas_h, cv::NORM_MINMAX);
            cv::normalize(hist_g, hist_g, 0, canvas_h, cv::NORM_MINMAX);
            cv::normalize(hist_r, hist_r, 0, canvas_h, cv::NORM_MINMAX);

            cv::Mat canvas2 = canvas.clone();
            canvas2.setTo(255);
            for(int i=1; i<binSize; i++){
                cv::line(canvas2,Point(pillar_w*(i-1),canvas_h - hist_b.at<float>(i-1)),Point(pillar_w*(i),canvas_h-hist_b.at<float>(i)),Scalar(255,0,0));
                cv::line(canvas2,Point(pillar_w*(i-1),canvas_h - hist_g.at<float>(i-1)),Point(pillar_w*(i),canvas_h-hist_g.at<float>(i)),Scalar(0,255,0));
                cv::line(canvas2,Point(pillar_w*(i-1),canvas_h - hist_r.at<float>(i-1)),Point(pillar_w*(i),canvas_h-hist_r.at<float>(i)),Scalar(0,0,255));
            }
            cv::imshow(canvas_name,canvas2);
        }
    };


    //原图分布
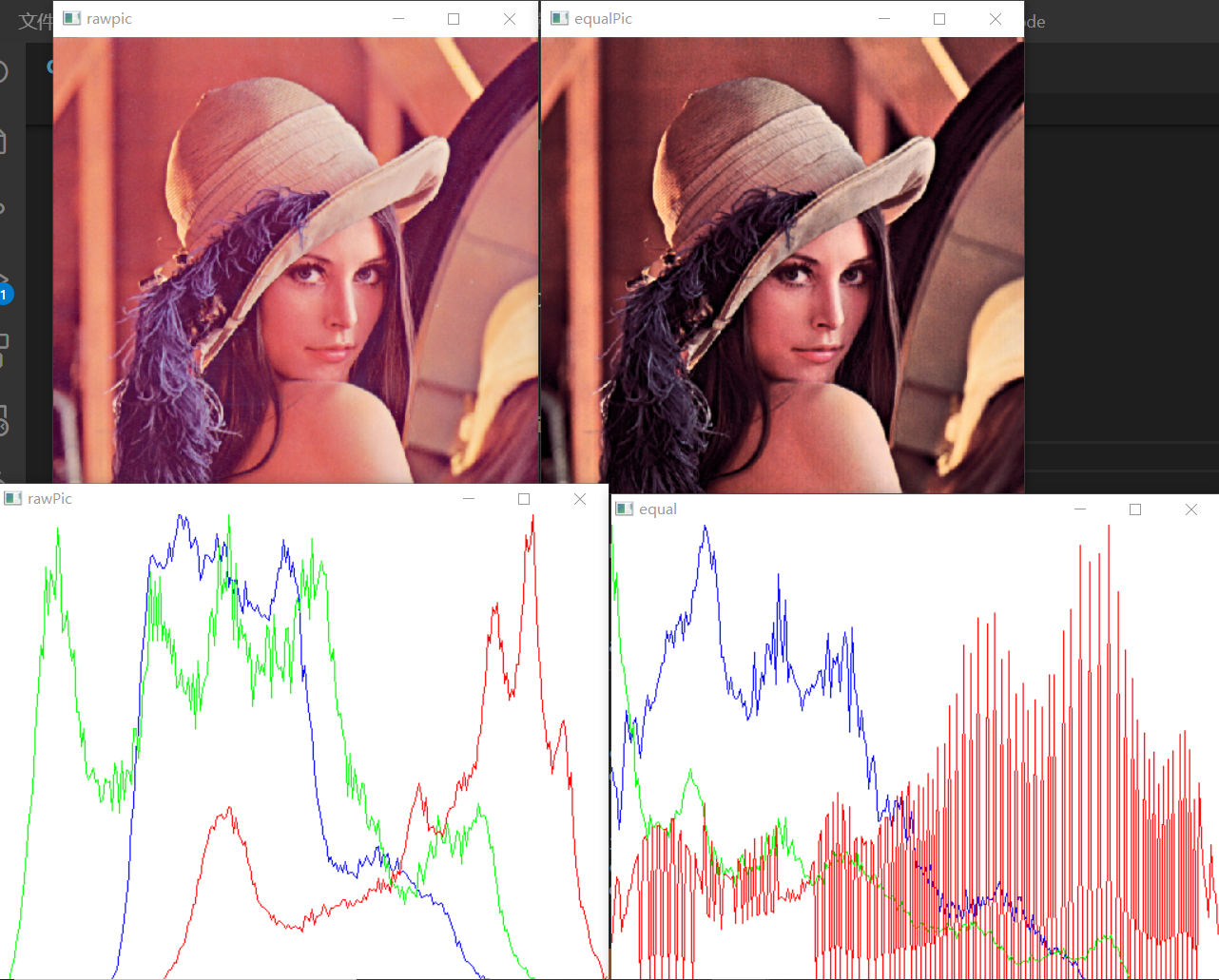
    calcHistAndDraw(rawPic,"rawPic"); 

    //HSV、均衡化处理
    cv::Mat equal;
    cv::cvtColor(rawPic,equal,cv::COLOR_BGR2HSV);
    std::vector<cv::Mat> equalSplit;
    cv::split(equal,equalSplit);
    cv::equalizeHist(equalSplit[2],equalSplit[2]);
    cv::merge(equalSplit,equal);
    cv::cvtColor(equal,equal,COLOR_HSV2BGR);
    cv::imshow("equal",equal);

    //均衡化后分布
    calcHistAndDraw(equal, "equal");

    cout<<"Done"<<endl;
    waitKey(0);
    cv::destroyAllWindows();
    return 0;
}

当然要知道，HSV不是唯一一种用于处理彩图的颜色空间，至少还有LAB和YUV空间可以用于这种处理，它们都是亮度和色彩分离的颜色空间；

限制对比度自适应直方图均衡化(Contrast Limited Adaptive HE，CLAHE)

直方图均衡化算法有一个颇为严重的问题来自分布函数的累积性，当一张图像具有大量的集中像素，容易产生过曝现象。这容易理解，例如当10灰度占了90%像素，这部分像素直接被提升到255×0.9灰度，即图像强行将黑像素提升到白像素，在图像中往往表现为引入噪声而丢失图像细节，在数据上则表现为具有高的突峰，毕竟均衡化对低分辨的灰度调整有限。

图像增强领域有一种经典的算法——CLAHE算法。CLAHE算法其实可以划分成两种独立算法，分别是CLHE算法和AHE算法，这也对应两种优化思路：

CLHE：限制对比度算法。过曝本质是像素过高，均衡化不能完全抹平突峰，因此CLHE的思路是定义一个图像阈值，当新像素灰度高于这个阈值时，截断为这个阈值，高出部分求和，这个sum除以总灰度级，加在每个灰度的像素灰度上。
AHE：自适应算法，同自适应二值化类似，它不对整张图片进行全局的HE操作，而是将图片分割成若干块，典型值是分割成8×8小块(注意不是图像分成64块，而是每个小块含64个像素)，在每个块中独立进行HE计算，由于这种分块求值得到的像素容易形成块状分布（即块内像素灰度差异极小、块间差异较大，马赛克效应），因此这里HE后的像素灰度还不算最终灰度，而是使用双线性插值来均衡这种效果：每个像素将参考它们离附近四个小块的距离权重，来计算新像素值。

OpenCV提供了一个CLAHE指针对象来实现这个算法：

cv::Ptr<cv::CLAHE> createCLAHE(
    double clipLimit = (40.0), //限制灰度阈值
    cv::Size tileGridSize = cv::Size(8, 8) //分割小块大小
)

//example:
    Mat rawPic = imread("D:/Documents/Desktop/note/jLena10.jpeg",0);
    cv::Ptr<cv::CLAHE> clahe = cv::createCLAHE(40,Size(8,8));
    cv::Mat dst;
    clahe->apply(rawPic,dst);
    cv::imshow("clahe",dst);

参考链接：