OpenCV C++记录(八)：Sobel、Scharr、Laplacian、Canny算子

Sobel算子

Sobel算子是一种边缘检测算子，由Irwin Sobel在1968斯坦福的博士生讨论会提出，在那个不重视论文和专利的年代，作者也没有为此发表论文，只在后来一本专著中公开，从此广泛被学界和工业界引用了几十年。

图像处理中经典的3阶Sobel卷积核常常表述为x方向和y方向，分别为：

此处我们发现零行两侧的系数恰好是相反数，尽管一些博客中矩阵调换了两侧符号顺序，只影响差分顺序，并不影响最终的差分结果。

Sobel算子的推导我查阅了大量博客资料，发现大多摘自电子科大彭真明教授的Sobel算子的数学基础，彭教授的参考来自文献，主要问题来自公式解读不同，以此图为坐标系：

原文公式为： 其中(1,1)、(-1,1)、(0,1)、(1,0)来自四个方向相邻点的方向向量，既然仅考虑了相邻点，所以这里是一种前向差分，前向差分表述为： 对于四分一、二分一，这里彭教授认为是一种城市距离(city-block distance)，几种常见距离定义如下图：

距离定义

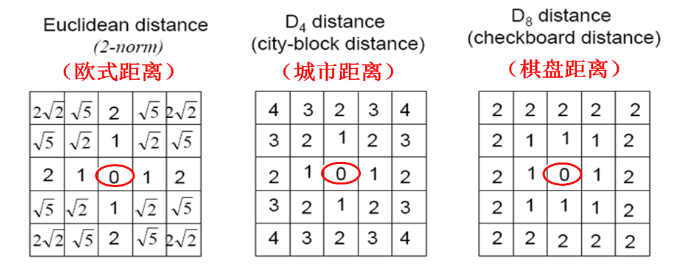
根据文献意图，四个方向梯度计算完成，还需要除以4以获取平均梯度，浮点数的矩阵运算是麻烦的，因此原文甚至将该结果乘4(以消除上面的四分一、二分一)，得到了两个反向增大了16倍系数矩阵，也即上述Sobel算子表达式。总而言之，彭教授将该式子解读为城市距离+前向差分的使用。

另一说法是通过欧氏距离和中心差分得到，对于3×3的Sobel卷积核，城市距离和欧氏距离的区别仅在对角线城市距离恰为欧氏距离的倍，而恰巧，这个能恰好被约去，推导过程如下：定义四个方向单位向量分别为(1,0)、(0,1)、、，这里的单位化实际上应用了中心差分，表述为： 因此，重新描述G的数学关系：

其中是对角线的欧式距离，该式与原文也是等效的，该法在Sobel边缘检测算子数学原理再学习被提出并用于推导5×5大小的Sobel算子，然而我竟没有找到标准5×5大小的Sobel算子，暂无法断言哪种实现是合乎现实的。

Sobel边缘检测

对图像进行Sobel处理，实际上是执行了二维卷积(注意并非矩阵乘法)，假设图像A，则 得到梯度在数学上应该是平方和再开方（即L2范数），但为了提高处理效率仅使用其绝对值和（即L1范数）：

OpenCV的边缘检测采用了阈值判断策略，当grad超过一定阈值，则认为出现边缘，对应像素会被置白；根据卷积性质，假设采用3×3的卷积核，恰好能计算一张3×3图片的中心像素梯度，其他像素的计算也就是需要进行边值填充处理了。而且卷积核越大，其对边缘敏感度越高，因此可能导致边缘误检越多。

OpenCV的Sobel算子支持单独应用横向或者纵向梯度，其中x方向的梯度可以检测纵向的边缘轮廓，y方向梯度用于检测横向边缘轮廓，接口如下：

void Sobel(
    cv::InputArray src, //输入图像，彩图/灰图等
    cv::OutputArray dst, //输出梯度图（边缘图
    int ddepth, //图像深度，宜使用支持负数、长度足够的，例如16S、32F/64F等
    int dx, int dy, //均取0——2，表示无操作、一阶二阶导，不能同时为0
    int ksize = 3, //卷积核大小，3、5、7等；
    double scale = (1.0), //输出梯度scale*grad+delta，适当调整两个系数因子可以调节效果
    double delta = (0.0), 
    int borderType = 4 //边值填充，默认4即BORDER_REFLECT_101
) 

BORDER_CONSTANT和BORDER_REPLICATE之前用过，补充之前没提的几种borderType：效果参考几种边值效果

• BORDER_REFLECT：在边界形成镜像反射；

• BORDER_REFLECT_101：类似上述，但不会反射边缘像素；

• BORDER_WRAP：当前边界外反射的是另一侧的边缘像素。

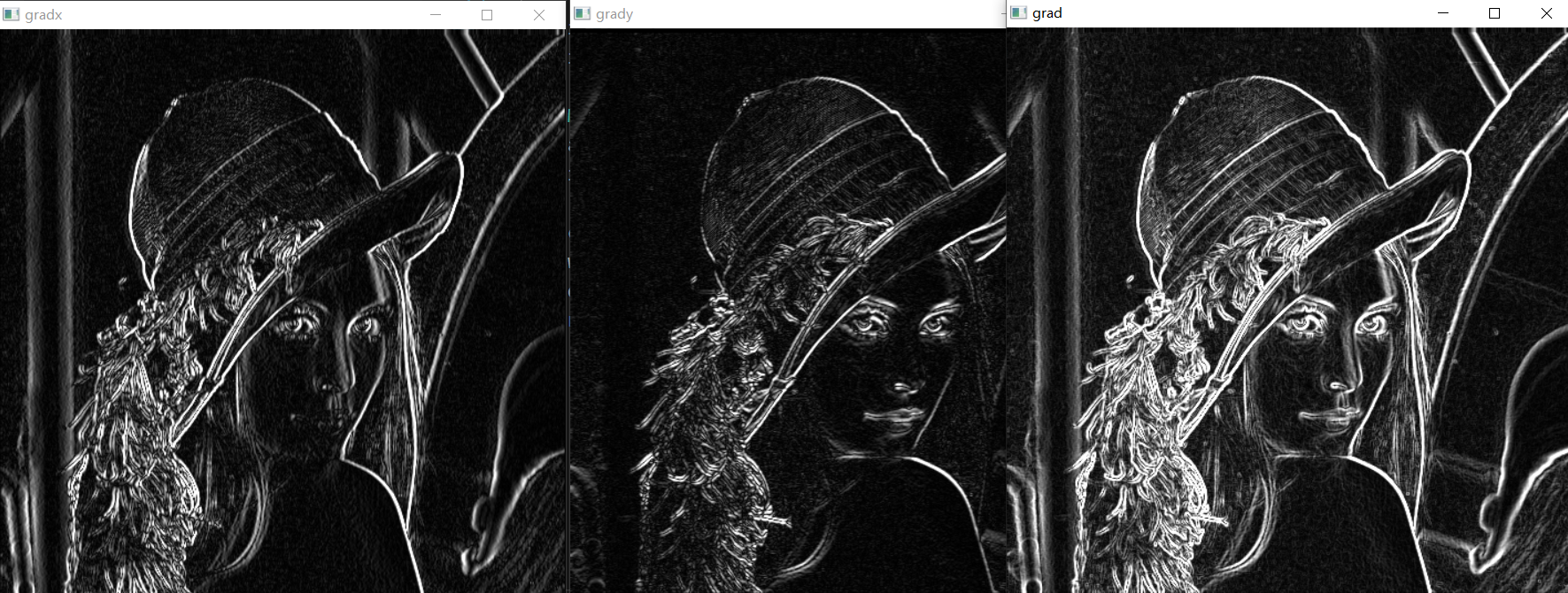
Sobel算子效果如下：

#include <iostream>
#include <opencv2/opencv.hpp>
#include <vector>

using namespace std;
using namespace cv;

int main(){

    Mat inputPic = imread("D:\\Documents\\Desktop\\note\\jLena.jpeg");
    Mat gray;
    cvtColor(inputPic,gray,COLOR_BGR2GRAY);
    Mat gradx,grady; //虽然但是，Sobel也支持三通道图
    Sobel(gray,gradx,CV_32F, 1 , 0, 3); //仅x方向，纵向轮廓
    Sobel(gray,grady,CV_32F, 0 , 1, 3); //仅y方向，横向轮廓

    convertScaleAbs(gradx,gradx); //负数取绝对值，转换到uint8灰度，这是线性映射而非截断
    convertScaleAbs(grady,grady);

    imshow("gradx",gradx);
    imshow("grady",grady);

    Mat grad;
    addWeighted(gradx,1 ,grady, 1, 0, grad); //梯度叠加
    imshow("grad",grad);

    cout<<"Done"<<endl;
    waitKey(0);
    destroyAllWindows();
    return 0;
}

Sobel算子

Scharr算子

Sobel算子在提取图像时，不调节scale和beta参数，提取的图像是偏黑的，说明它提取图像内部边缘轮廓能力较差，Scharr算子增大了卷积核的权值来优化提取，具体提取原理和Sobel是大同小异的，水平和垂直算子分别为：

Scharr边缘检测

参数唯一的区别是Scharr去除了卷积核大小ksize的选择，只能是大小为3的卷积核：

void Scharr(
    cv::InputArray src, //输入图像，彩图/灰图等
    cv::OutputArray dst, //输出梯度图（边缘图
    int ddepth, //图像深度，宜使用支持负数、长度足够的，例如16S、32F/64F等
    int dx, int dy, //均取0——2，表示无操作、一阶二阶导，不能同时为0
    double scale = (1.0), //输出梯度scale*grad+delta，适当调整两个系数因子可以调节效果
    double delta = (0.0), 
    int borderType = 4 //边值填充，默认4即BORDER_REFLECT_101
) 

代码将原来Sobel名字改掉去除ksize参数即可，得到效果：

Laplacian算子

Sobel和Scharr算子都是一阶算子，它们的原理就是做一阶差分来估计梯度，尽管它们能指定二阶参数，也很少直接将它们归纳到二阶算子，而拉普拉斯则是常见的二阶明星算子，在数学、物理界尤其常见，图像处理亦是如此。

从一阶到二阶，无非多了一次求导(离散则差分)，能够衡量梯度变化的快慢，也即灰度变化的快慢，对一阶算子而言通常只能找到那些灰度突变的轮廓，而二阶算子则能够获取到某个局部的像素极大值或极小值，这也容易理解，不严谨概括描述为二阶导数零点描述了一阶导数的起伏规律，如果一阶导数也存在零点那么可能将在灰度上表示成局部极大、极小值，因此二阶算子更精准获取获取边缘信息，但也注定其不具备单独获取X、Y方向能力、对噪声敏感等特点。

x方向和y方向的拉普拉斯算子表述为： 这里可以通过泰勒公式理解，离散和连续函数不同的是求导看成差分，连续的极小量h看成是邻近差分1： 可见提出二阶差分恰为上式。

OpenCV拉普拉斯算子是不支持单独方向的，这里组合表示：

矩阵表示为: 另一种版本考虑了四个角点，表示为： 此处将中心像素减去8是保证整体卷积核之和为0，因为在像素相同区域（代表颜色均匀），如果因为卷积核出现非均匀系数就会导致额外噪声引入；另一个特点，为什么要多考虑四个角点，这通常被认为是一种噪声平滑操作，在Sobel/Scharr算子中，除了差分核(-1 0 1)/(-3 0 3)，还有权值更大的平滑核(-2 0 2)/(-10 0 10)，它们赋予了中心像素两侧更大的权值，表示为对X、Y方向两侧无关像素噪声的抑制。对拉普拉斯算子亦是如此，缺少四个角点进行卷积，能够准确差分识别边缘，但是这种非均匀的卷积使其对噪声过于敏感，所以做了这样的优化。

拉普拉斯边缘检测

void Laplacian(
    cv::InputArray src, //输入彩图/灰度图
    cv::OutputArray dst, //输出图
    int ddepth, //输出图存储深度，宜深且支持负数，见前
    int ksize = 1, //默认3×3算子
    double scale = (1.0), //梯度结果scale*grad + delta
    double delta = (0.0), 
    int borderType = 4 //边值填充，默认4即BORDER_REFLECT_101
)

实例：

#include <iostream>
#include <opencv2/opencv.hpp>
#include <vector>

using namespace std;
using namespace cv;

int main(){

    Mat inputPic = imread("D:\\Documents\\Desktop\\note\\jLena.jpeg");
    Mat gray;
    cvtColor(inputPic,gray,COLOR_BGR2GRAY);

    Mat result;
    Laplacian(gray,result,CV_32F,1, -1);
    convertScaleAbs(result,result);
    imshow("Laplacian",result);

    cout<<"Done"<<endl;
    waitKey(0);
    destroyAllWindows();
    return 0;
}

Canny算子

走过了拉普拉斯这个明星算子，终于到了边缘检测的真神——Canny算子，Canny算子不再是一个简单的卷积核，它使用了一系列方法提高边缘检测的灵敏度，且保证了对噪声的抑制性，以及处理的鲁棒性，是边缘检测最常用的一种算子。

Canny算子通过四阶段的操作来检测边缘，首先使用5×5高斯核滤波对图像噪声进行抑制，然后使用Sobel算子计算梯度，再根据梯度大小和方向进行非极大值抑制(Non Maximum Suppression，NMS)，采用滞后阈值（双阈值筛选）方法进一步处理像素，滤波内容会在下一篇文章记录，这里只需要解释最后两个操作内容。

非极大值抑制

非极大值抑制NMS用于将边缘精细化处理，避免出现成块成白色区域的边缘情况，具体原理是当Sobel计算的梯度一致时，仅保留局部最大值结果，一个示意图如：

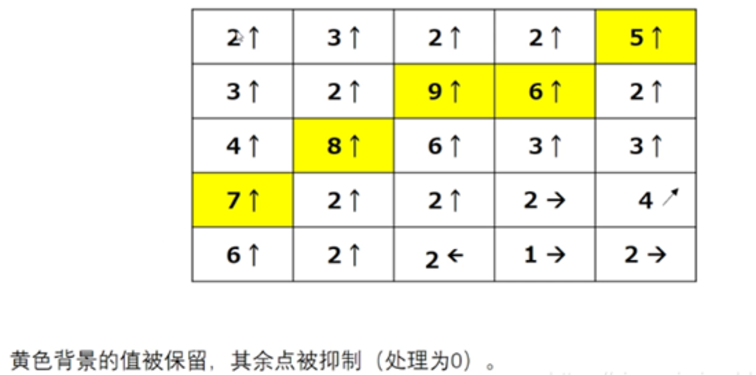
此处为了减少开销，OpenCV仅考虑了四个梯度方向，分别是0°、45°、90°、135°，例如22.5°与67.5°之间的梯度均被视作45度，沿着该方向画一条直线（左下->右上的直线），仅像素为直线方向上的极值，该像素才会被保留，并且可能被最终置白，一种NMS实现如下，由于arctan值域为，因此起点从-45°算起，以下（这里仅做了Sobel和NMS）：

#include <iostream>
#include <opencv2/opencv.hpp>
#include <vector>

using namespace std;
using namespace cv;

void nmsOperate(Mat& gradXY, Mat& gradX, Mat& gradY, Mat& result){
    result = gradXY.clone();
    for(int i=0; i<gradXY.rows; i++){ 
        for(int j=0; j<gradXY.cols; j++){
            double grad_x = gradX.ptr<uchar>(i)[j];
            double grad_y = gradY.ptr<uchar>(i)[j];

            double theta = atan(grad_y/grad_x);

            if(theta == 0)
                continue;

            double g0,g1;
            if(theta>-3*CV_PI/8 && theta< -CV_PI/8){
                g0 = gradXY.ptr<uchar>(i-1)[j-1];
                g1 = gradXY.ptr<uchar>(i+1)[j+1];
            }
            else if(theta>-CV_PI/8 && theta< CV_PI/8){
                g0 = gradXY.ptr<uchar>(i)[j-1];
                g1 = gradXY.ptr<uchar>(i)[j+1];
            }
            else if(theta>CV_PI/8 && theta< 3*CV_PI/8){
                g0 = gradXY.ptr<uchar>(i+1)[j-1];
                g1 = gradXY.ptr<uchar>(i-1)[j+1];
            }
            else{
                g0 = gradXY.ptr<uchar>(i-1)[j];
                g1 = gradXY.ptr<uchar>(i+1)[j];
            }
            if(gradXY.ptr<uchar>(i)[j]<=g0 || gradXY.ptr<uchar>(i)[j]<=g1)
                result.ptr<uchar>(i)[j] = 0;
        }
    }
}

int main(){
    Mat inputPic = imread("D:\\Documents\\Desktop\\note\\jLena.jpeg");
    Mat gray;
    cvtColor(inputPic,gray,COLOR_BGR2GRAY);

    Mat gradX,gradY,gradXY;
    Sobel(gray,gradX,CV_32F, 1, 0);
    Sobel(gray,gradY,CV_32F, 0, 1);

    convertScaleAbs(gradX,gradX); 
    convertScaleAbs(gradY,gradY);

    addWeighted(gradX,1 ,gradY, 1, 0, gradXY);

    imshow("gradX",gradX);
    imshow("gradY",gradY);
    imshow("gradXY",gradXY);

    Mat doNMS;
    nmsOperate(gradXY,gradX,gradY,doNMS);
    imshow("doNMS",doNMS);

    cout<<"Done"<<endl;
    waitKey(0);
    destroyAllWindows();
    return 0;
}

Sobel+NMS

滞后阈值

原理也比较简单，首先定义高阈值TH和低阈值TL，阈值比例常用3：1或2：1，像素灰度高于TH的仍然置255（强边缘），低于TL的一律置0，介于此二者的称为弱边缘（虚边缘），对于虚边缘，需要遍历其周围八个像素（八领域），如果存在至少一个强边缘，那么该像素会被置255；另一个细节问题是这种强化是否存在传递性，例如一个弱边缘被强化后是否意味着其八邻域某个弱边缘能进一步传递，答案似乎是肯定的，它不像DBSCAN算法那样仅允许一次的边界点传递行为，认为其利于描绘和构造轮廓。

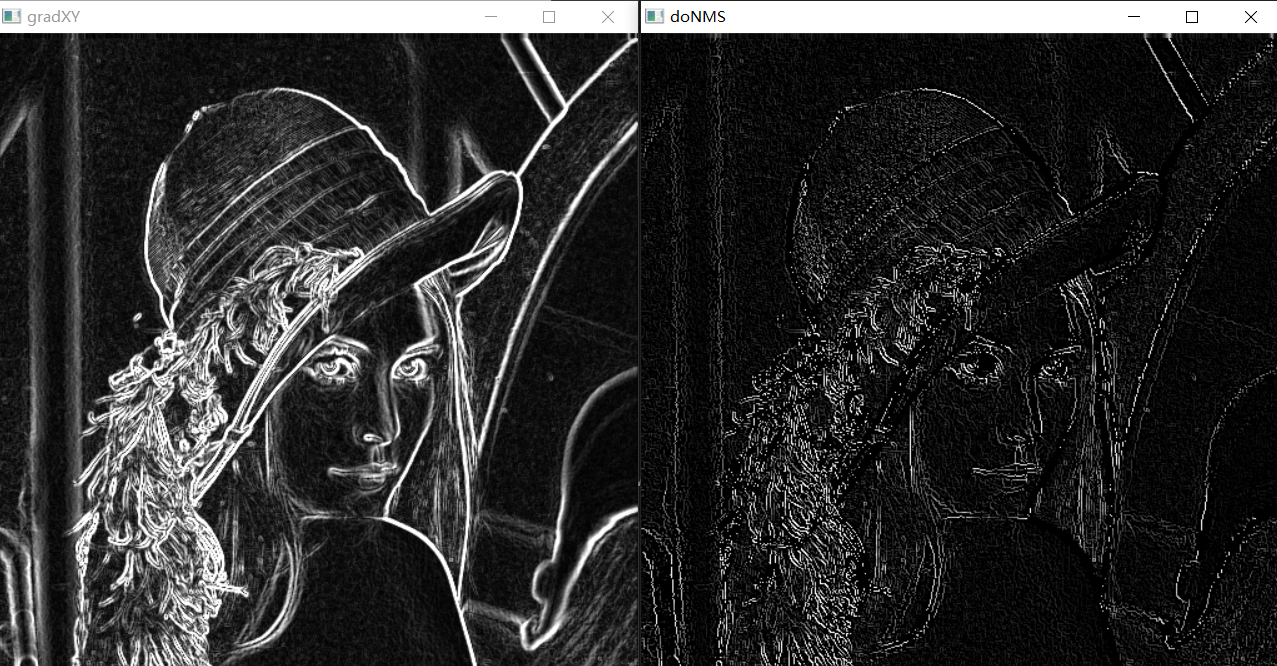
然而没有复现到和Canny相似的成果，可见CV源码是做了不少的工作上的优化，也可能是上述传递行为的方向性我没有处理好，既然没有Canny的效果这里就不放源码了误导了，仅把山寨和原版结果进行呈现，值得一提的是有的CV Canny并没有内置高斯滤波，因此如果对其再进行一次高斯滤波，会得到更加简洁的效果：

Canny

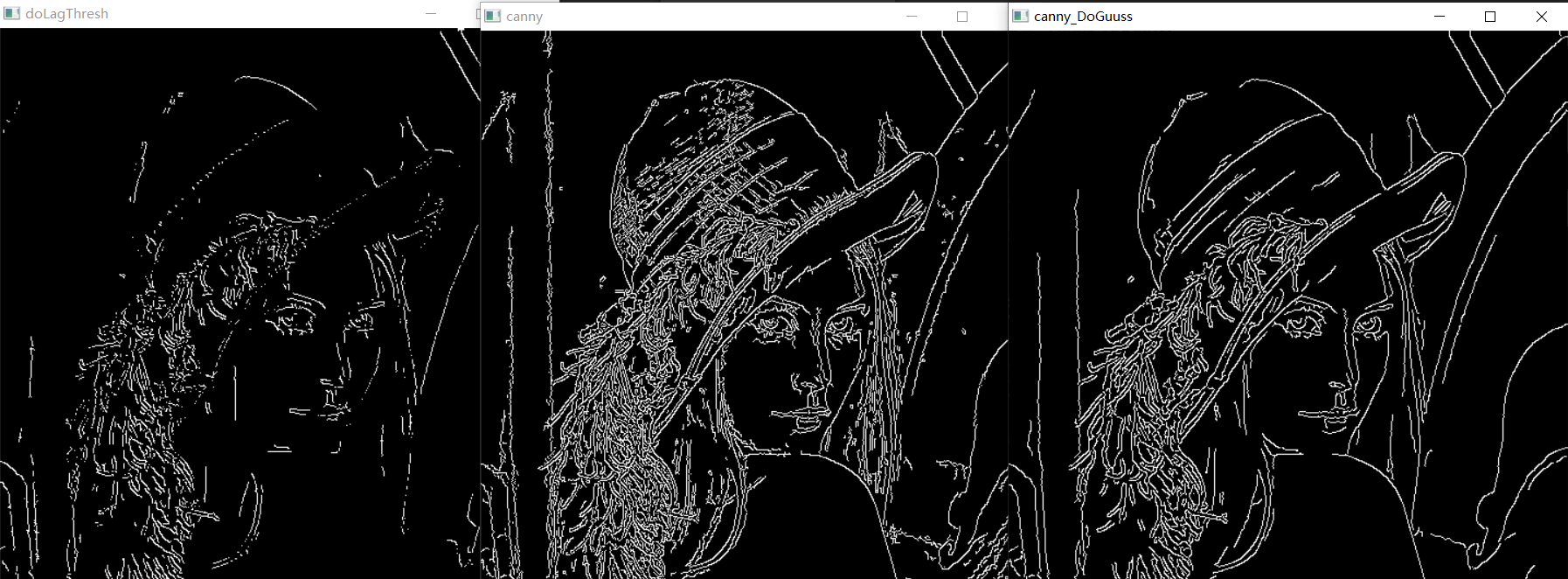
cv::Canny用法以下。

OpenCV Canny边缘检测

Canny的参数比较简单：

void cv::Canny(
    InputArray image, //输入图像
    OutputArray edges, //输出图像
    double threshold1, //低阈值
    double threshold2, //高阈值
    int apertureSize = 3, //Sobel算子卷积核大小，3、5、7等
    bool L2gradient = false //是否使用L2范数刻画梯度，准确但性能略低
);

Mat inputPic = imread("D:\\Documents\\Desktop\\note\\jLena.jpeg");
Mat gray;
cvtColor(inputPic,gray,COLOR_BGR2GRAY);

Mat canny;
Canny(gray,canny,50,100,3,false);
imshow("canny",canny);

参考链接：

1. Sobel算子

2. Sobel算子的数学基础

3. Sobel边缘检测算子数学原理再学习

4. OpenCV-C++ Sobel算子使用

5. 通俗理解拉普拉斯算子

6. 前向差分、后向差分和中心差分误差分析

7. OpenCV 笔记(12)：常用的边缘检测算子—— Canny