OpenCV C++记录(七)：霍夫变换、仿射变换、透视变换
霍夫变换(Hough Transform)
霍夫变换只是一种特征变换，服务于图像霍夫直线、圆的检测，这两种图形是霍夫变换最常用的两个应用，也算基本图形，基于此扩展霍夫检测能识别图像中几乎所有的几何图形。
对人而言判断一条直线或者某种图形是非常直接简单的，而对于计算机而言，它获取的信息是像素，如何确定某一群像素就是一条共线的直线、一个圆形，如果出现像素外溢，如何辨认出这种偏差影响，是比较复杂的任务，也是霍夫变换的基本任务。
霍夫直线检测基本原理
假设给定两点像素坐标(x1,y1)和(x2,y2)，可知过两点得到一条直线y = kx + b，这是笛卡尔空间的表达式，重新描述这个表达式:
b = -xk + y，自变量为k、因变量为b，该空间称为霍夫空间，对于笛卡尔坐标的两点(x1,y1)和(x2,y2)，分别对应b = -x1k + y1和b = -x2k + y2，即对应霍夫空间两条线，且x1不等于x2的情况下（相等的情况后文再讨论），两条霍夫空间直线必然交与一点，该点(b0,k0)同时满足两条霍夫直线方程，故知(b0,k0)就是原式y = kx + b的解。
因此，一句话表述就是，通过两点，需要获取y = kx + b直线的解(斜率、截距)，实际上就是求解霍夫空间的相交点。
可能会有人不禁要问，两个点直接拟合不就好了吗，注意这里我们只使用了两点像素做说明，实际上的图片成千上万的像素，如果在笛卡尔空间筛选、拟合、回归是比较复杂的，而在霍夫空间中，这些像素点变成了直线，不同的像素点去拟合一条直线，实际上只是求解这些直线的相交点，如果像素点并不严格组成一条直线，在霍夫空间中则表现为出现多个交点，统计经过这些交点的直线数，选取最多直线经过的一个，就是最后的拟合结果，这被称为霍夫变换的投票机制，在标准霍夫变换中，累加器(Accumulator)会统计经过点的直线数，超过一定阈值才会被认为是一个直线。
当x1 = x2时，在b-k霍夫空间中无法交于一点，因此采用极坐标重新描述映射关系，令x = ρcosθ，y = ρsinθ，换到ρ-θ霍夫空间为：
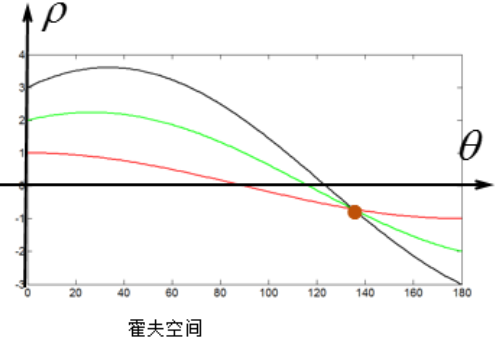
综述，不同像素的笛卡尔坐标组成的直线总能在霍夫空间找到相交的交点，该点就是直线的参数。
霍夫圆检测基本原理
实际上也是类似的，平面圆的自由度为3，分别是x、y坐标和半径长度r，因此其笛卡尔空间解析式在霍夫空间中成为三维交点，被空间直线穿过最多的三维交点，就是最后该平面圆的参数。基于此也可获知霍夫变换可应用于其他更复杂的图形检测任务，例如椭圆，其自由度是5，分别是x、y坐标和a、b长短轴以及旋转角度θ，原理上它对应的是五维空间的一个点参数，但直接计算可能复杂度过高，一般会有其他策略（梯度策略）来处理这样的检测任务,后文我们介绍OpenCV的处理。
OpenCV实现
OpenCV霍夫直线检测
OpenCV提供了cv::HoughLines和cv::HoughLinesP函数执行霍夫直线相关检测，对应了三种霍夫变换检测方法，分别是标准霍夫变换(Standard
Hough Transform，SHT)、多尺度霍夫变换(Multi-Scale Hough
Transform，MSHT)、累积概率霍夫变换(Progressive
Probabilistic Hough Transform，PPHT)。
SHT和MSHT都是关于函数cv::HoughLines：仅MSHT会使用参数srn和stn来降低距离和角度的分辨率
1
2
3
4
5
6
7
8
9
10
11void cv::HoughLines(
InputArray image, // 输入图像（二值化，通常为边缘检测后的图像）
OutputArray lines, // 输出直线参数（ρ, θ）的向量，注意是极坐标描述的,且为法向量
double rho, // 距离分辨率（单位：像素），推荐为1.0
double theta, // 角度分辨率（单位：弧度），推荐为pi/180
int threshold, // 累加器阈值（判定为直线的阈值）
double srn = 0, // 多尺度霍夫变换的 rho 除数（若为0，则为标准霍夫变换）
double stn = 0, // 多尺度霍夫变换的 theta 除数（若为0，则为标准霍夫变换）
double min_theta = 0, // 检测的最小角度（0）
double max_theta = CV_PI // 检测的最大角度（π）
);
累积概率霍夫变换也是旨在优化SHT的概率，其通过随机采样来检测边缘中的像素，而不会使用累加器去统计每一个像素，从而降低统计的开销；更重要的是它能获取直线的端点信息，而SHT则没有检测端点的功能，因此PPHT一般用于线段检测；再者cv::HoughLinesP输出的lines数组以直角坐标系给出，而非SHT中的极坐标法向量；
PPHT直线检测函数如下： 1
2
3
4
5
6
7
8
9void cv::HoughLinesP(
InputArray image, // 输入图像（二值化，通常为边缘检测后的图像）
OutputArray lines, // 输出线段参数（起点和终点坐标）
double rho, // 距离分辨率（单位：像素）
double theta, // 角度分辨率（单位：弧度）
int threshold, // 累加器阈值（判定为线段的阈值）
double minLineLength = 0, // 线段的最小长度（小于此值的线段被丢弃）
double maxLineGap = 0 // 线段之间的最大间隔（小于此间隔的线段会被合并）
);
SHT直线检测
这里要注意，SHT没有识别端点的功能，描述平面直线的方法是描述它的法向量，输出的lines正是存储该法向量，假设为(a,b)，因此直线的方向向量应该是(-b,a)，我们定义了极大量10000，相当于往方向向量两端延申，就绘制出这条直线；这里还使用了Canny做边缘检测，这通常是目标检测、轮廓提取等前置处理，具体原理将在不久后的文章补充。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
using namespace std;
using namespace cv;
int main(){
Mat inputPic = imread("D:\\Documents\\Desktop\\note\\chess.jpg");
Mat gray;
cv::cvtColor(inputPic,gray,COLOR_BGR2GRAY); //灰度化
imshow("gray",gray);
cv::Mat edges;
cv::Canny(gray, edges, 50, 150); //Canny边缘检测
vector<Vec2f> lines; //直线法向量，分别是极径rou、与x轴夹角theta
HoughLines(edges, lines, 1, CV_PI/180, 200); //阈值200才输出直线
for (int i = 0; i < lines.size(); i++) {
float rou = lines[i][0], theta = lines[i][1];
Point pt1, pt2;
double a = cos(theta), b = sin(theta); //法向量(a,b)
double x0 = a*rou, y0 = b*rou; //直线上一点
pt1.x = cvRound(x0 + 10000*(-b)); //方向向量是(-b,a)，假设延申10000像素为绘制直线的端点
pt1.y = cvRound(y0 + 10000*(a));
pt2.x = cvRound(x0 - 10000*(-b));
pt2.y = cvRound(y0 - 10000*(a));
line(inputPic, pt1, pt2, Scalar(0, 0, 255), 1, LINE_AA); //连线
}
imshow("line",inputPic);
cout<<"Done"<<endl;
waitKey(0);
destroyAllWindows();
return 0;
}
效果：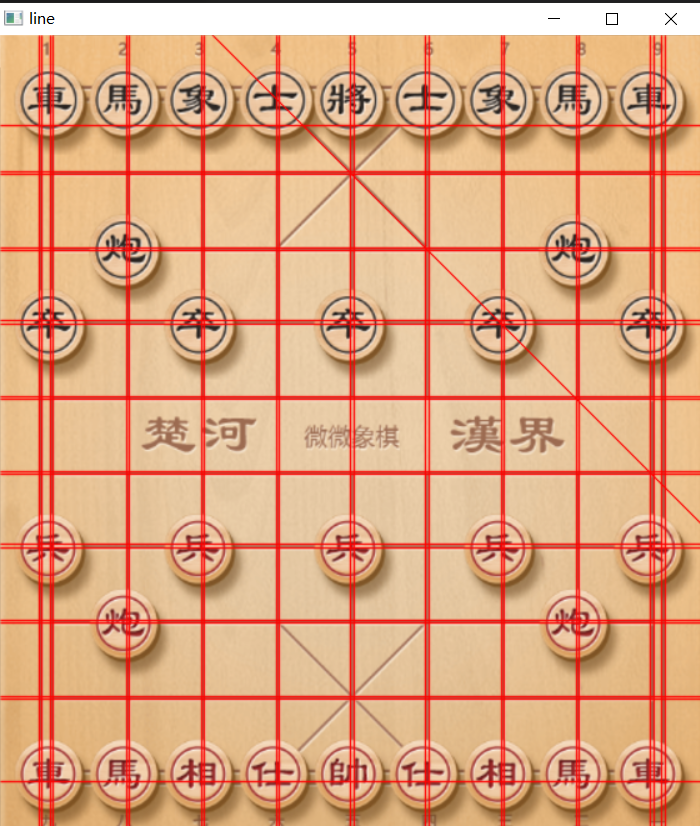
PPHT直线检测
cv::HoughLinesP输出的是线段的起点和终点坐标：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
using namespace std;
using namespace cv;
int main(){
Mat inputPic = imread("D:\\Documents\\Desktop\\note\\chess.jpg");
Mat gray;
cv::cvtColor(inputPic,gray,COLOR_BGR2GRAY); //灰度化
imshow("gray",gray);
cv::Mat edges;
cv::Canny(gray, edges, 50, 150);
vector<Vec4i> lines;
HoughLinesP(edges, lines, 1, CV_PI/180, 100,50,10);
for(int i=0; i<lines.size(); i++){
Point pt1,pt2;
pt1 = Point(lines[i][0],lines[i][1]);
pt2 = Point(lines[i][2],lines[i][3]);
line(inputPic, pt1, pt2, Scalar(0,0,255), 1, LINE_AA);
}
imshow("line",inputPic);
cout<<"Done"<<endl;
waitKey(0);
destroyAllWindows();
return 0;
}
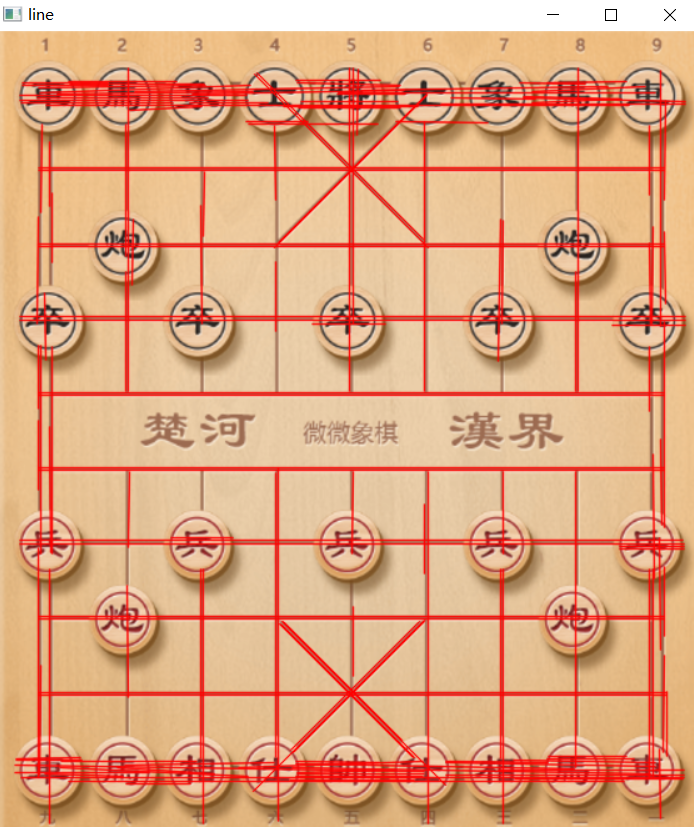
OpenCV霍夫圆检测
正如上面说过，圆的自由度是3，SHT情况下求解是这样的：圆在笛卡尔坐标表达式为：
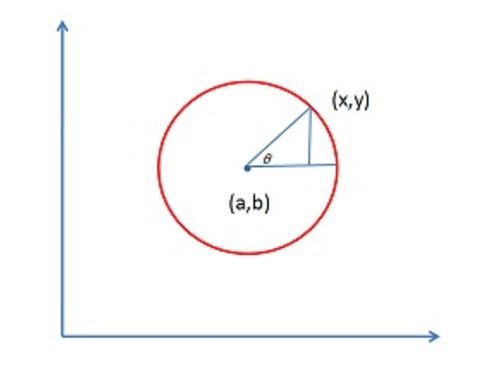
从霍夫空间来看，不同的(a,b,r)参数组合的是一个圆锥体面，投票并统计这些锥面的三维交点就是参数结果。
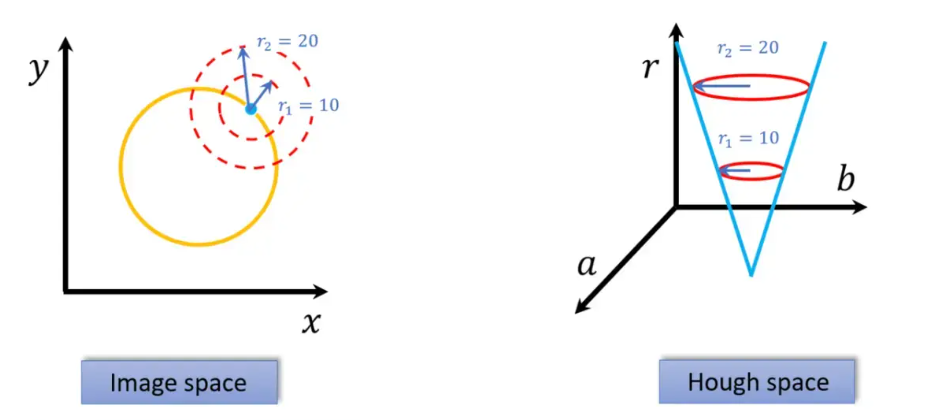
SHT就说到这里，从维度上增加一维，计算的复杂度却大大增加，因此OpenCV没有使用SHT，而采用的是一种降维方法——霍夫梯度法（Hough Gradient Method）。
霍夫梯度法
霍夫梯度法将圆的参数估计划分成两个阶段，分别是圆心估计和半径估计：
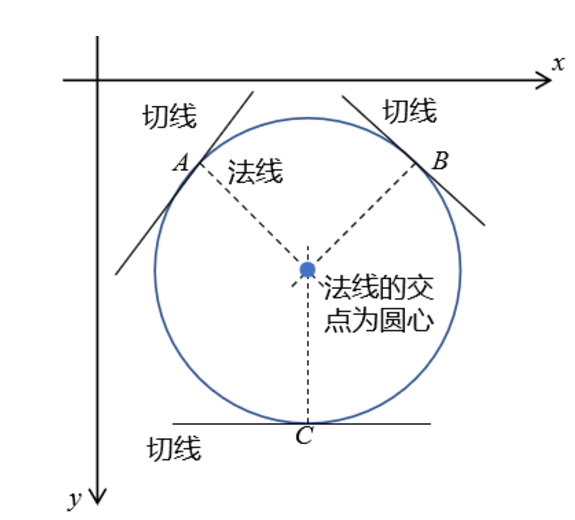圆心估计：首先假设我们拿到了圆周像素（边缘像素），这些像素都可以看成构成圆周的一段“小切线”，根据线画圆的原理，两条切线的垂直平分线即可确定圆心。OpenCV中，通过Canny边缘检测可以拿到圆周像素，要求切线的法向量，实际上就是求像素的梯度（注意梯度方向就是方向导数最大的方向），这里引入Sobel算子进行计算（这也在不久后的文章中介绍），已知边缘像素的法向量，根据设定的最大和最小的可能的圆半径，将对每个候选圆心进行投票，得到最后的圆心；
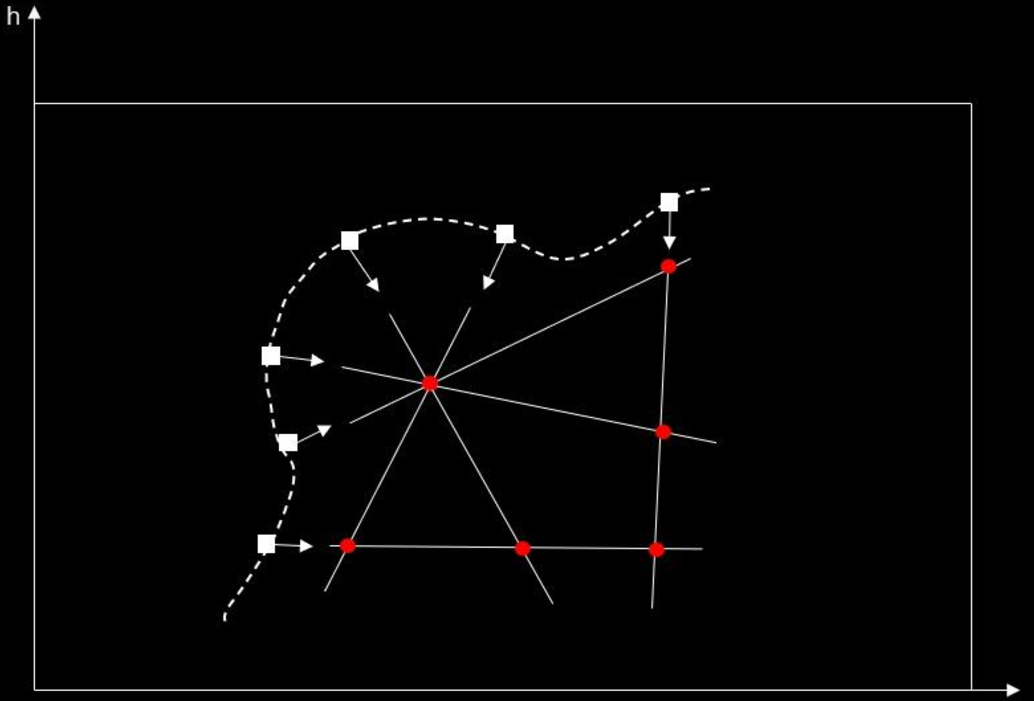
半径估计：得到圆心后只需要再根据圆心和边缘像素距离进行累计投票（圆心离各边缘像素的距离应该是一致的），即可得到半径长度。
可见三维的估计任务转换成梯度-半径二维估计问题，因此提高了计算效率和鲁棒性。
OpenCV的接口为： 1
2
3
4
5
6
7
8
9
10
11void cv::HoughCircles(
InputArray image, //一般是灰度图，必须是单通道
OutputArray circles, //输出圆心、半径(x,y,r)
int method, //仅支持梯度方法cv::HOUGH_GRADIENT
double dp, //一般为1或2，1代表分辨率同图像，2代表为图像一半，dp越大：分辨率越低、精度越差、计算越快
double minDist, //圆心最小距离，防止重叠严峻
double param1, //Canny的高阈值，低阈值为param1/2
double param2, //累加器阈值，越低检测出对象越多
int minRadius, //最小圆半径
int maxRadius //最大圆半径
)
霍夫圆检测实例： 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
using namespace std;
using namespace cv;
int main(){
Mat inputPic = imread("D:\\Documents\\Desktop\\note\\chess.jpg");
Mat gray;
cv::cvtColor(inputPic,gray,COLOR_BGR2GRAY); //灰度化
imshow("gray",gray);
vector<Vec3f> circles;
HoughCircles(gray, circles, cv::HOUGH_GRADIENT, 1, 10, 100, 60, 10, 50);
for(int i=0; i<circles.size(); i++){
Point pt0 = Point(cvRound(circles[i][0]),cvRound(circles[i][1]));
int r = cvRound(circles[i][2]);
circle(inputPic, pt0, r, Scalar(0,0,255), 3, LINE_AA);
}
imshow("circle",inputPic);
cout<<"Done"<<endl;
waitKey(0);
destroyAllWindows();
return 0;
}
仿射变换(Affine Transformation)
仿射变换应该是一个并不陌生的概念，以往我们在两个地方常常听到这个名词。其一是高中的圆锥曲线，通过将椭圆仿射到圆去求解一些几何问题，其二是人脸识别任务中，当遇到非正脸的识别常见，我们常常加入仿射变换使得各个特征点和正脸图片对齐，再执行识别。
仿射变换的数学原理描述为：假设图像像素坐标为(x,y)，对其做这样的运算得到映射到新坐标：
a11是将x坐标进行缩放，a22是对y坐标进行缩放，a12是对x方向的两条边进行反方向拉动（正方形->平行四边形），a21是对y方向两条边反方向拉动（正方形->平行四边形），tx、ty则是分别向x、y方向进行平移。可见仿射变换是一种线性变换。
因此，原地变换相当于：
平移矩阵
仅使用平移、旋转的仿射变换几乎没有改变图像的相关特征，例如任意两点距离、两线的夹角、对象形状，因此这两种操作也是称为刚性变换（欧几里得变换）。
平移矩阵是最好理解的：
旋转矩阵
这个是根据极坐标推导的，令
OpenCV仿射变换
然后就可以理解CV仿射变换的操作了，CV提供了cv::warpAffine函数进行仿射变换计算，其中变换矩阵将上述旋转、平移系数合并在一个2×3矩阵，因为仿射变换可能出现定义外的像素，也需要插值和边值处理。
1
2
3
4
5
6
7
8
9void cv::warpAffine(
InputArray src, // 输入图像
OutputArray dst, // 输出图像
InputArray M, // 2x3 变换矩阵
Size dsize, // 输出图像的大小
int flags = INTER_LINEAR, // 插值方法
int borderMode = BORDER_CONSTANT, // 边界填充模式
const Scalar& borderValue = Scalar() // 边界填充值
);
图像平移
图像右下平移(50,100): 1
2
3
4
5
6
7
8Mat_<float> pan = (Mat_<float>(2,3)<< //平移
1,0,50,
0,1,100
);
Mat output;
warpAffine(rawPicColor,output,pan,rawPicColor.size(),INTER_LINEAR,BORDER_CONSTANT,Scalar(0,0,0));
imshow("Pan",output);
图像旋转
这里一个特别的地方是进行旋转是默认是相对(0,0)坐标进行的，因此不能直接使用公式定义图片旋转操作，CV提供了cv::getRotationMatrix2D可用于定义旋转矩阵，接受几何中心（设置为图像中心）、逆时针角度（顺时针为负）、缩放因子，最后使用cv::warpAffine旋转变换：
1
2
3
4
5//注意中心，cols在前，rows在后，逆时针45度
Mat rotate = cv::getRotationMatrix2D(Point(rawPicColor.cols/2,rawPicColor.rows/2),45,0.5);
Mat output;
warpAffine(rawPicColor,output,rotate,rawPicColor.size(),INTER_LINEAR,BORDER_CONSTANT,Scalar(0,0,0));
imshow("rotate",output);
图像放缩
除了刚性变换，仿射变换还可以完成图像缩放等处理:x方向拉伸两倍、y方向缩小至0.5倍：
1
2
3
4
5
6
7
8Mat_<float> resize_ = (Mat_<float>(2,3)<<
2,0,0,
0,0.5,0
);
Mat output;
warpAffine(rawPicColor,output,resize_,rawPicColor.size(),INTER_LINEAR,BORDER_CONSTANT,Scalar(0,0,0));
imshow("resize_",output);
透视变换(Perspective Transformation)
仿射变换最大的特点是它是一种线性变换，例如在原来图像中平行的两个对象，变换后也一定是平行的。透视变换则是一种非线性变换，我们的图像处理大多数来自三维空间需求，在三维成像中近大远小是基本规律，物体在远处的光线总是收敛的，导致这种视图就像梯形一样甚至发生相交，透视变换能利用非线性变换来描述两种视角的关系，这个非线性变换是一个3×3的矩阵，称单应性矩阵H。
透视变换是一个二维——三维——二维的过程，至于哪个二维是正视角，在工程中好像并不重要，反正透视变换透过三维空间完成了一组二维视角的转换。假设原始二维坐标为(x,y)，透视后变换后坐标为(x2,y2)，现在我们开始描述其数学过程：
因为是空间三维变换，我们将(x,y)表示为(x,y,1)，表示其始终在z=1的图像平面，再与单应性矩阵运算：
此时单应性矩阵可以表示为：
再拓展，仿射变换实际上是透视变换的一个子集，仿射变换矩阵可表示为：
OpenCV透视变换
cv::getPerspectiveTransform通过四个源点和四个目标点即可计算其八个映射参数：
1
2
3
4
5Mat getPerspectiveTransform(
InputArray src, //4个源点
InputArray dst, //4个目标点
int solveMethod = DECOMP_LU //求解线性方程组方法，默认即可
) cv::warpPerspective即可完成透视变换：
1
2
3
4
5
6
7
8
9void warpPerspective(
InputArray src, //源图
OutputArray dst, //输出图像
InputArray M, //透视变换矩阵
Size dsize, //输出图像大小
int flags=INTER_LINEAR, //插值方法
int borderMode = BORDER_CONSTANT, //边值处理方法
const Scalar& borderValue = Scalar() //边值处理默认颜色
)；
透视变换实例：
1 |
|
效果：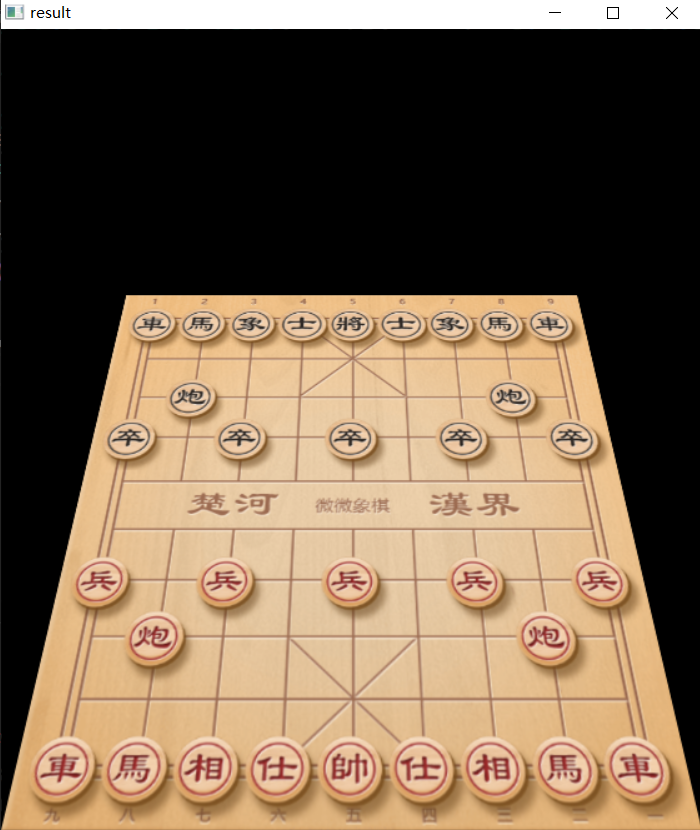 
通过透视变换实现了到另一个二维视角的转换。
参考链接：
