OpenCV C++记录(五)：插值算法：最近邻插、双线性插值、双三次插值

插值算法

图像放缩的过程也是像素增加、减小的过程，因此需要插值算法、采样算法等，在保证一定性能的基础上争取较好的输出质量。记录几种方法原理，对应OpenCV中几种常用插值算法，分别是最近邻插值、双线性插值、双三次插值，其性能依次递减，效果依次递增，其中双线性插值是二者比较均衡的算法，是许多插值模型的默认模式。如果对原生插值算法无兴趣，可直接跳过本文，看简单的放缩函数，不小心引出这么一大段，我想也是比较扯蛋，但终归有所收获。

最近邻插值INTER_NEAREST

最近邻插值最大的特点是：不会产生新的像素，目标图像的像素均来自源图像，新图像坐标与源图像坐标对应如下:

例如将2*2的图片放大成4*8的图片，新图(3,8)位置的像素计算：故取原图(2,2)位置的像素。

最近邻插实现图像放大：由于我先完成了双三次和双线性插值算法再回头写这个，有些问题反而在篇头省略了。例如这里的int y_ = round((i+0.5)*scale_y-0.5)等详见后文《双线性插值优化》讨论，是一种几何中心对齐，主要是用于纠正计算参考点时几何中心偏差。

#include <iostream>
#include<opencv2/opencv.hpp>

using namespace std;
using namespace cv;

//三通道输入图像、目标高度、宽度
Mat getNearestMat(Mat& src_mat, int target_height, int target_width){
    Mat result(target_height,target_width,src_mat.type()); //目标矩阵

    //缩放尺度
    double scale_x = (double)src_mat.cols/(double)target_width;
    double scale_y = (double)src_mat.rows/(double)target_height;

    for(int i=0; i<target_height; i++){
        int y_ = round((i+0.5)*scale_y-0.5);  //参考点y_: 目标像素y在源矩阵的投影坐标
        //截断y范围
        y_ = y_ >= src_mat.rows ? src_mat.rows-1 : (y_ < 0 ? 0 : y_);
        for(int j=0; j<target_width; j++){
            int x_ = round((j+0.5)*scale_x-0.5); //参考点x_: 目标像素x在源矩阵的投影坐标
            //截断x范围
            x_ = x_ >= src_mat.cols ? src_mat.cols-1 : (x_ < 0 ? 0 : x_);
            result.at<Vec3b>(i,j)[0] = src_mat.at<Vec3b>(y_,x_)[0]; //三通道
            result.at<Vec3b>(i,j)[1] = src_mat.at<Vec3b>(y_,x_)[1];
            result.at<Vec3b>(i,j)[2] = src_mat.at<Vec3b>(y_,x_)[2];
        }
    }
    return result;
}


int main(){
    Mat rawPic = imread("C:\\Users\\24364\\C_git\\opencv_test\\jLena.jpg",1);
    imshow("rawPic",rawPic); //原始：512×512

    Mat NearestMat = getNearestMat(rawPic,1024,1024); //放大两倍
    imshow("NearestMat",NearestMat);

    cout<<"Done";
    waitKey(0);
    destroyAllWindows();

    return 0;
}

效果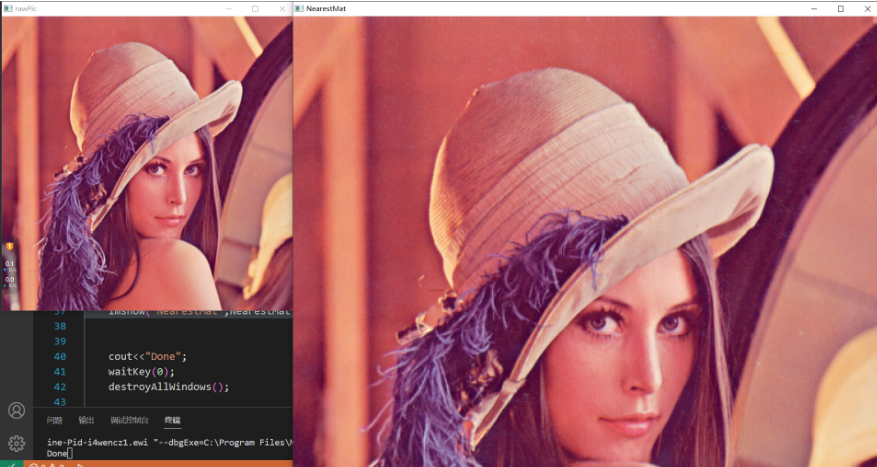：最近邻插值肉眼看起来也效果不算太差，值得一提的是，OpenCV的最近邻插和本文的方法应该是有差异的，在非整数变换时输出不一致的结果，具体差异有待参详源码。后文实现的双线性插值和双三次插值则基本没有该问题，只是OpenCV会做更多的并行计算优化。

双线性插值INTER_LINEAR

对于双线性插值，第一步和最近邻插值是一样的，只是不再简单地进行四舍五入了。假设现在仍然得到(srcX=1.5,srcY=1.75)的结果，可知这点落在原图的四点像素之间，分别是(1,1)、(1,2)、(2,1)、(2,2)，现在需要基于此四点确定原图点(1.5,1.75)像素，这个点的像素是四点像素的混合权值和，这就是双线性插值的基本问题。

回顾线性插值问题，基于两个点取确定一点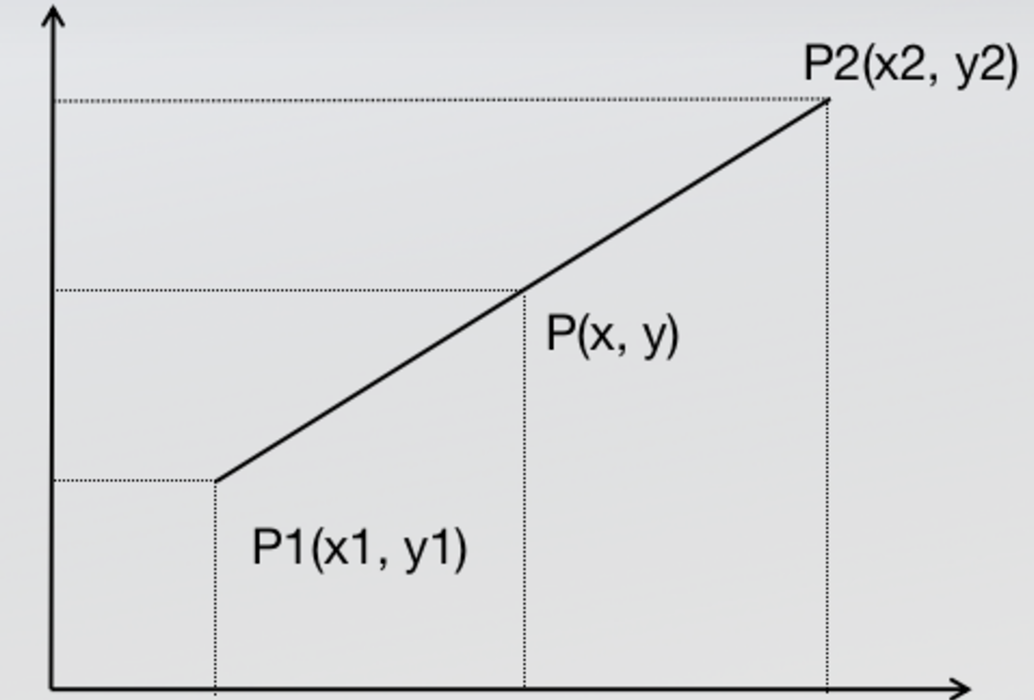：一维插值假设y=f(x),其中x为一维坐标，f(x)为该坐标的像素，有：得：

应该体会到，一条线段(一维空间)的x坐标确定，此点的像素y也是确定的。

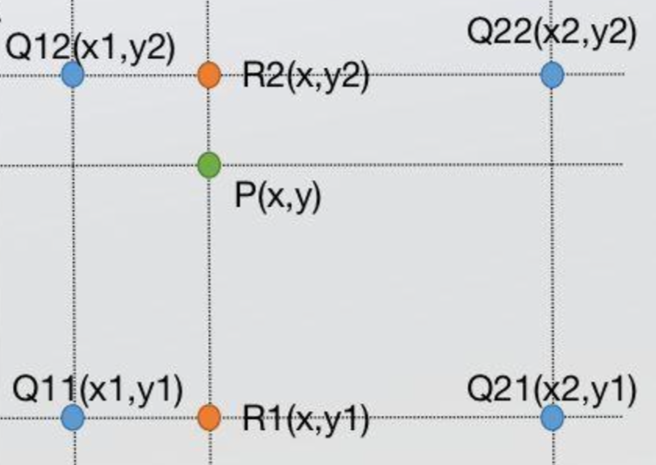双线性插值现在问题是平面上一个点(x,y)，如何确定其像素，没必要将问题说成二维问题，仍然按照一维的描述，只需要两个辅助点即可，Q11、Q21是确定的，因此R1像素可以由插值法求得，同理R2亦可由插值法求得，那么P就是R1、R2线段的插值结果，也即双线性插值实际上做了三次单线性插值，其中两次是x方向，一次y方向(取法不唯一)。

分别列出公式，因为方向不同，x、y均被占用，记Q11-Q21、Q12-Q22、R1-R2像素分布函数f1(x)、f2(x)、f3(y)，R1、R2、P像素为z1 = f1(x),z2 = f2(x),z3 = f3(y),三条一维插值公式应该是：

因为线性插值，对于f1、f2、f3像素分布，其和自变量x/y一定是唯一对应的，R1像素既可以表示为f1(x)，也可以是f3(y1)，因此有: 所以将z1、z2带入z3，而且双线性插值均是取源图相邻像素，因此x2-x1 = 1,y2-y1 = 1，就得到了P像素的表达式（其中下式分母部分全为1**，为了完整性没有简化掉）:

其中f1(x1)、f1(x2)、f2(x1)、f2(x2)对应四个像素点像素，将分式写成权重，P像素进一步写成:

双线性插值的优化

根据最近邻插值的公式，问题是会带来几何中心的偏移：例如一个3*3图像的中心是(1,1)，放大至7*7后，中心(3,3)元素应该对应源图(1,1)，但是根据公式计算得约(1.286，1.286)，几何中心向右下角偏移；

再次强调线性插值像素和位置应该是一一对应的，这种差异会带来些许的颜色偏移，但在卷积计算中这种偏移会导致整体的固有误差，应该避免。

OpenCV定义了一种权重分布来纠正这种误差，公式更新为：

还有另一个问题也应该知晓：在双线性插值中，图像放缩时并不是对每个像素都是公平的，例如按照旧公式来看从一个3*3图像放大至7*7后，一般以左上角第一个元素为(0,0)坐标，扩大操作新图像的(0,0)坐标像素就是源图的(0,0)，而(6,6)却对应(2.57,2.57)，注意3*3的最后一个像素应该是(2,2)，说明对应关系发生了越界，而且是左右不均衡的。

以优化公式计算，这种不公平的偏移也得到了均衡，新图(0,0)对应的是(-0.2857,-0.2857),(6,6)对应的是(2.2857,2.2857)。

对于边界像素越界问题，不仅是双线性插值，而且卷积运算(滤波等操作)都会遇到，OpenCV也定义了处理边界外像素的相关策略，例如设置恒定常数、取最近像素等，参考Image Filtering《boxFilter》函数。在最近邻插中，因为没有新像素（大小均来自原来存在的像素），因此直接做了截断，而在双线性插值和双立方插值中，需要基于填充图计算新像素，因此需要考虑边界填充。

双线性插值实现

在使用上面的公式计算目标像素在源矩阵的参考坐标时，假设矩阵宽高均从4放大到5，我们会发现(0,0)对应的是(-0.1,-0.1)，但是源矩阵根本不存在这个坐标像素，因此我们只需要做一个边值填充，因此我们先对4×4的源矩阵边缘做了size=2的padding，成为了8×8的矩阵。按新坐标系，5×5目标矩阵的(0,0)对应的参考点应该是(1.9,1.9)，进而我们的纠正公式修正为：

C++边界填充函数：

void cv::copyMakeBorder(
    InputArray src,
    OutputArray dst,
    int top, //四个方向填充像素
    int bottom,
    int left,
    int right,
    int borderType,
    const Scalar& value = Scalar() //填充类 型：BORDER_CONSTANT常数填充、BORDER_REPLICATE最近像素填充等
)

代码：实现单通道的双线性插值浮点数：

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

//双线性插值
Mat getBilinerMat(Mat& src_mat, int target_height, int target_width){
    //尺度
    double scale_x = (double)src_mat.cols/(double)target_width;
    double scale_y = (double)src_mat.rows/(double)target_height;

    //填充
    int padSize = 2;
    copyMakeBorder(src_mat,src_mat,padSize,padSize,padSize,padSize,BORDER_REPLICATE);

    Mat result(target_height,target_width,src_mat.type());

    for(int i=0; i<target_height; i++){
        double y_ = (i+0.5)*scale_y + 1.5; //参考点y坐标
        int round_y = round(y_+0.5);  //计算y_+0.5四舍五入后每次都会对齐到y2像素，y2-1就是y1像素，方法不唯一
        for(int j=0; j<target_width; j++){
            double x_ = (j+0.5)*scale_x + 1.5; //参考点x坐标
            int round_x = round(x_+0.5);  //同y原理

            int x1 = round_x-1; int y1 = round_y-1; //四邻域
            int x2 = round_x; int y2 = round_y;

            double w1 = (y2-y_)*(x2-x_);//权值计算
            double w2 = (y2-y_)*(x_-x1);
            double w3 = (y_-y1)*(x2-x_);
            double w4 = (y_-y1)*(x_-x1);
            //计算(i,j)的像素
            result.at<double>(i,j) = w1*src_mat.at<double>(y1,x1) + w2*src_mat.at<double>(y1,x2) + \
                                     w3*src_mat.at<double>(y2,x1) + w4*src_mat.at<double>(y2,x2);
            }
        }
    return result;
}

int main(){
    RNG rng;
    Mat rawMat(4,4,CV_64FC1);
    rng.fill(rawMat,RNG::UNIFORM,0,255);
    cout<<"Raw Mat:\n"<<rawMat<<endl;

    Mat sysBiliner,myBiliner;
    resize(rawMat,sysBiliner,Size(5,5),0,0,INTER_LINEAR);
    cout<<"sysBiliner Mat:\n"<<sysBiliner<<endl;

    myBiliner = getBilinerMat(rawMat,5,5);
    cout<<"myBiliner Mat:\n"<<myBiliner<<endl;

    cout<<"Done"<<endl;
    return 0;
}

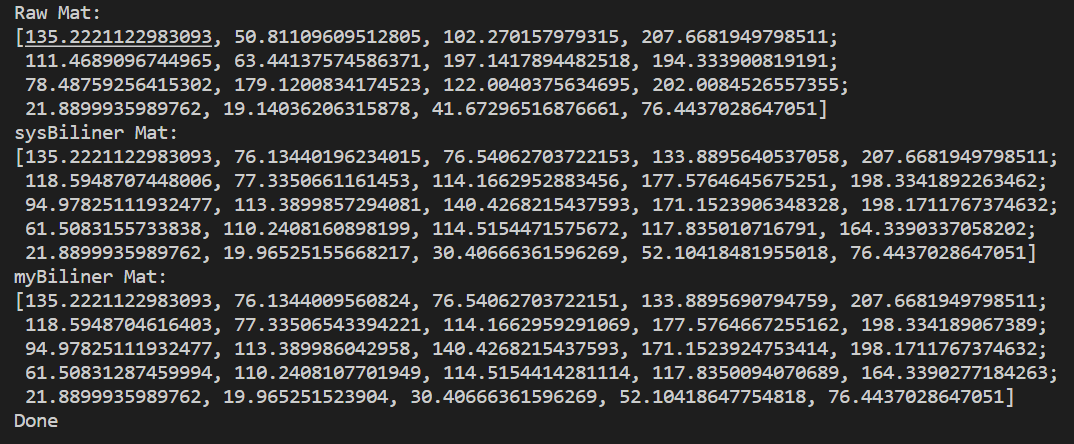
从结果来看，和系统方法只有浮点精度差异：双线性插值浮点数比较

图像双线性插值

变换到三通道就可以了：

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

//双线性插值
Mat getBilinerMat(Mat& src_mat, int target_height, int target_width){
    //尺度
    double scale_x = (double)src_mat.cols/(double)target_width;
    double scale_y = (double)src_mat.rows/(double)target_height;

    //填充
    int padSize = 2;
    copyMakeBorder(src_mat,src_mat,padSize,padSize,padSize,padSize,BORDER_REPLICATE);

    Mat result(target_height,target_width,src_mat.type());

    for(int i=0; i<target_height; i++){
        double y_ = (i+0.5)*scale_y + 1.5; //参考点坐标
        int round_y = round(y_+0.5);
        for(int j=0; j<target_width; j++){
            double x_ = (j+0.5)*scale_x + 1.5; //参考点坐标
            int round_x = round(x_+0.5);

            int x1 = round_x-1; int y1 = round_y-1;
            int x2 = round_x; int y2 = round_y;
            double w1 = (y2-y_)*(x2-x_);
            double w2 = (y2-y_)*(x_-x1);
            double w3 = (y_-y1)*(x2-x_);
            double w4 = (y_-y1)*(x_-x1);

            //三通道
            result.at<Vec3b>(i,j)[0] = w1*src_mat.at<Vec3b>(y1,x1)[0] + w2*src_mat.at<Vec3b>(y1,x2)[0] + \
                                        w3*src_mat.at<Vec3b>(y2,x1)[0] + w4*src_mat.at<Vec3b>(y2,x2)[0];

            result.at<Vec3b>(i,j)[1] = w1*src_mat.at<Vec3b>(y1,x1)[1] + w2*src_mat.at<Vec3b>(y1,x2)[1] + \
                                        w3*src_mat.at<Vec3b>(y2,x1)[1] + w4*src_mat.at<Vec3b>(y2,x2)[1];

            result.at<Vec3b>(i,j)[2] = w1*src_mat.at<Vec3b>(y1,x1)[0] + w2*src_mat.at<Vec3b>(y1,x2)[20] + \
                                        w3*src_mat.at<Vec3b>(y2,x1)[2] + w4*src_mat.at<Vec3b>(y2,x2)[2];
        }
    }
    return result;
}

int main(){
    //图片插值
    Mat rawPic = imread("C:\\Users\\24364\\C_git\\opencv_test\\jLena.jpg",1);
    imshow("rawPic",rawPic);

    Mat myBiliner = getBilinerMat(rawPic,1024,1024);
    imshow("myBiliner",myBiliner);

    waitKey(0);
    destroyAllWindows();
    cout<<"Done"<<endl;
    return 0;
}

效果和最近邻插是基本相似的，肉眼上也看不到明显差异，就不放图了。

双三次插值INTER_CUBIC

权值计算输出矩阵

双三次插值，又称双立方插值，算法采用了像素点邻近16个像素点样本进行权重计算，因为是三阶平滑，考虑到了双立方插值没有考虑的灰度变化率问题，因此平滑效果一般比前二两种算法好。但也带来了大量的复杂图像运算。

可以从两种角度描述计算的数学方法；

对应位置相乘

假设现有4×4源矩阵放大成5×5目标矩阵，尝试计算目标矩阵(2,2)位置像素，利用前述双线性插入纠正公式计算参考点的公式：得到参考点应该是(1.5,1.5)，取该参考点附近的16个像素(恰好就是源矩阵本身)，获取两个方向的权值矩阵(具体方法下一节展开)，总而言之分别得到了代表X方向（水平方向）、y方向（垂直）两个4×4矩阵，将两个矩阵对应位置和源矩阵对应位置相乘（注意这不是矩阵乘法），得到最后的4×4矩阵再将矩阵内部元素求和，此值即目标矩阵(2,2)的像素值。

矩阵乘法

上述对应位置相乘，在数学上用矩阵乘法表示，则X权值矩阵是4×1矩阵、Y权值矩阵是1×4矩阵，目标像素值满足：

    elem = Y*src_matrix*X

最后输出是一个1×1矩阵，该值即是目标像素值。

为什么Y矩阵既是4×4矩阵，又是1×4矩阵，看完下节方法会清晰，Y作为4×4矩阵时，每行的数值是一样的。

一些文章将公式写为三个4×4矩阵的乘法，实在有点误人子弟，由线性代数可知上述公式才是正确的行变换与列变换写法。

获取权值

给出双三次插值的权重公式：

$，，，$

其中a为系数，Matlab中取-0.5，OpenCV中定义的是-0.75；

在cv源码中中三次插值使用的系数是:

coeffs[0] = ((A*(x + 1) - 5*A)*(x + 1) + 8*A)*(x + 1) - 4*A;
coeffs[1] = ((A + 2)*x - (A + 3))*x*x + 1;
coeffs[2] = ((A + 2)*(1 - x) - (A + 3))*(1 - x)*(1 - x) + 1;
coeffs[3] = 1.f - coeffs[0] - coeffs[1] - coeffs[2];

可见coeffs[0]是1<|x|<2公式的坐标变换，coeffs[1]、coeffs[2]是

时的坐标变换；coeffs[3]看起来比较玄学，展开后实际上得到coeffs[3]=A*x*x-A*x*x*x，它也是一个坐标变换，见下文。

开始时我也不理解为什么cv要进行这样的坐标变换，后面才知道这是通过偏移获取权重，首先看一下权重计算常规方法：

double getWeight(doubl**e num){
    const float a = -0.75;
    double n = abs(num); //绝对值
    //公式获取权重
    double w = ((a+2)*pow(n,3)-(a+3)*pow(n,2)+1)*(n<=1)+\ 
        (a*pow(n,3) - 5*a*pow(n,2)+8*a*n-4*a)*(n>1&&n<2);
    return w;
}

//输入矩阵、参考点的x坐标、y坐标，计算X、Y方向的权值
Mat getWeightMatrix(Mat input,double baseline_x,double baseline_y){
    Mat result(input.rows,input.cols,CV_64FC1);
    if(!result.isContinuous()) //不连续，谨慎处理
        return {};
    for(int i=0; i<input.rows; i++){
        double weightX = getWeight(i-baseline_x);
        for(int j=0; j<input.cols; j++){
            double weightY = getWeight(j-baseline_y);
            result.at<double>(i,j) = weightX*weightY;
        }
    }
    return result;
}

然而这种方法计算一个参考点，就需要多次进行公式计算，而实际上因为双三次插值只是16个邻域，两个方向各自只有4个系数。

因此另一种方法，仅看x坐标（这里代表列），双三次插值的元素来自邻近四列数据，，与所求点的坐标差值一定分别是-2到-1、-1到0、0到1、1到2；例如一个源矩阵4*4矩阵放大成5*5目标矩阵，目标矩阵(2,2)对应源矩阵位置应该是(1.5,1.5)，x方向离0、1、2、3列距离分别是-1.5、-0.5、0.5、1.5；y方向同理。

故知，从x方向上，权重公式只和列数相关，y方向则只和行数相关，令参考点位置（x0,y0）向下取整（位置上是向左上角）得到(u,v)，参考点离其距离列和行分别是(Δx,Δy)，即(x0,y0)=(u+Δx,v+Δy)，例**如(1.5,1.5)=(1,1)+(0.5,0.5)；

因此x方向，四列与参考点的分布依次是|1+Δx|、|Δx|、|1-Δx|、|2-Δx|（0<=Δx<=1），因为自变量是带绝对值的，因此无需讨论谁正谁负，因此对于每列权值均有：

coeffs[0] = W(1+Δx) = Ax*x*x - 2A*x*x + A*x;
coeffs[1] = W(Δx) = (A+2)x*x*x - (A+3)*x*x + 1;
coeffs[2] = W(1-Δx) = -(A+2)x*x*x + (2A+3)*x*x - A*x;
coeffs[3] = W(2-Δx) = A*x*x-A*x*x*x

也就是说，OpenCV源码中的四个参数中的x，实际上就是此处的Δx，二者的展开应该是相等的。

双三次插值的边值填充与完整算法

这部分思路主要参考插值算法｜双三次插值算法，也比较清晰易懂，本文也会加以说明。如下。

现在开始处理边界像素，因为对于5×5目标矩阵，计算发现(0,0)对应的参考点是(-0.1,-0.1)，是无法使用getObjectPixel函数获取像素值的，因为这是越界像素，且没有充足的4×4邻域去双三次插值，因此我们先对4×4的源矩阵边缘做了size=2的padding，成为了8×8的矩阵。后边的原理就几乎不变了，现在按新坐标系，5×5目标矩阵的(0,0)对应的参考点应该是(1.9,1.9)，进而我们的纠正公式修正为：

利用这个padding矩阵，就可以填充目标矩阵的所有像素了，如下：

注意上述讲解，将x讨论成行，但是图像处理习惯使用x遍历图像的列，使用y遍历图像的行，因此代码中是y矩阵*16点矩阵乘*x矩阵，Δy代表垂直方向偏差。手搓代码时也应该注意这些差异。

#include <iostream>
#include<opencv2/opencv.hpp>

using namespace std;
using namespace cv;

//接收源矩阵、参考点坐标，输出目标像素
double getObjectPixel(Mat input,double baseline_x,double baseline_y){
    // input.convertTo(input,CV_64FC1);
    auto getWeight = [](int i,double x)->double{ //此处传入x是delta x或delta_y
        const float a = -0.75; 
        if(i==0) //相当于coeffs[0]
            return a*x*x*x - 2*a*x*x + a*x;
        else if(i==1) //coeffs[1]
            return (a+2)*x*x*x - (a+3)*x*x + 1;
        else if(i==2) //coeffs[2]
            return -(a+2)*x*x*x + (2*a+3)*x*x - a*x;
        else if(i==3) //coeffs[3]
            return a*x*x-a*x*x*x;
        else
            return 0.0;
    };

    //左上角取整
    int stemp_x = floor(baseline_x);
    int stemp_y = floor(baseline_y);

    double delta_x = baseline_x - stemp_x;
    double delta_y = baseline_y - stemp_y;

    Mat xWeight(4,1,CV_64FC1);
    Mat yWeight(1,4,CV_64FC1);

    for(int i=0; i<4; i++){
        xWeight.at<double>(i,0) = getWeight(i,delta_x);
        yWeight.at<double>(0,i) = getWeight(i,delta_y);
    }

    //计算参考点附近十六个点矩阵,矩阵为参考点四舍五入的左2、右2、上2、下2范围
    int x_round = round(baseline_x+0.5);
    int y_round = round(baseline_y+0.5);
    Mat Mat16_ = input(Range(y_round-2,y_round+2),Range(x_round-2,x_round+2));

    // Mat Mat16_ = input(Range(stemp_y-1,stemp_y+3),Range(stemp_x-1,stemp_x+3));
    Mat result = yWeight*Mat16_*xWeight;
    // result.convertTo(result,CV_8UC1);
    return result.at<double>(0,0); //Y权重*十六点矩阵*X权重矩阵，最后输出1×1矩阵就是(baseline_x,baseline_y)的像素
}

Mat getTargetMatrix(Mat& mSrc, int target_width, int target_height){
    //填充
    int padSize = 2;
    Mat mPad;
    copyMakeBorder(mSrc,mPad,padSize,padSize,padSize,padSize,BORDER_REPLICATE);
    Mat mResult(target_height,target_width,CV_64FC1);
    double scale_x = ((double)mSrc.cols/(double)target_width);
    double scale_y = ((double)mSrc.rows/(double)target_height);
    for(int i=0; i<target_height; i++){
        double y_temp = (i+0.5) * scale_y + 1.5;
        for(int j=0; j<target_width; j++){
            double x_temp = (j+0.5) * scale_x + 1.5;
            mResult.at<double>(i,j) = getObjectPixel(mPad,x_temp,y_temp);
        }
    }
    return mResult;
}
int main(){
    RNG rng;
    Mat rawMat(4,4,CV_64FC1);
    rng.fill(rawMat,RNG::UNIFORM,0,256,0);

    cout<<"row Matrix:\n"<<rawMat<<endl;

    Mat mybiCubic,sysbiCubic;
    mybiCubic=getTargetMatrix(rawMat,5,5); // 个人方法

    resize(rawMat,sysbiCubic,Size(5,5),0,0,INTER_CUBIC);//系统方法

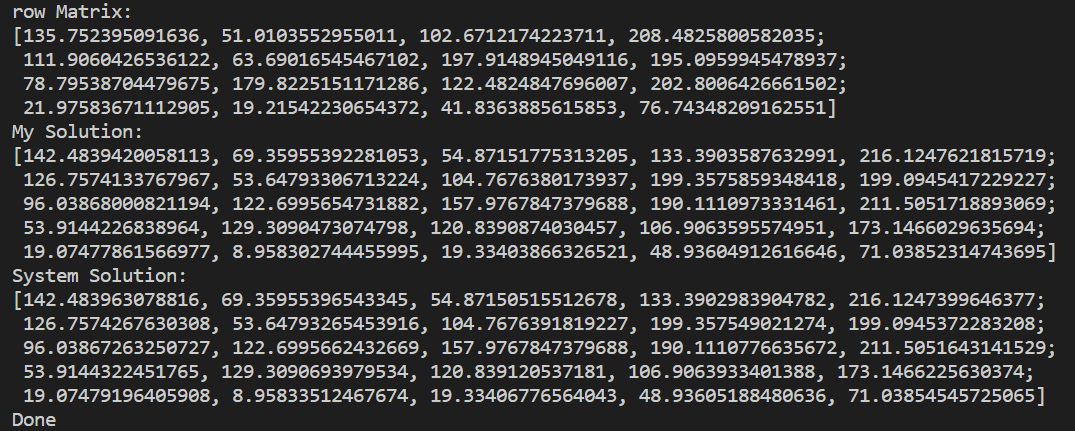
    cout<<"My Solution:\n"<<mybiCubic<<endl;
    cout<<"System Solution:\n"<<sysbiCubic<<endl;

    cout<<"Done";
    return 0;
}

将输出矩阵和系统的双三次插值方法进行比较，可知步骤是基本正确的：双三次插值比较

同样原理，转换到三通道上，就能够得到插值放大的图片结果：

#include <iostream>
#include<opencv2/opencv.hpp>

using namespace std;
using namespace cv;

//接收源矩阵、参考点坐标，输出目标像素
vector<double> getObjectPixel(Mat input,double baseline_x,double baseline_y){
    // input.convertTo(input,CV_64FC1);
    auto getWeight = [](int i,double x)->double{ //此处传入x是delta x或delta_y
        const float a = -0.75; 
        if(i==0) //相当于coeffs[0]
            return a*x*x*x - 2*a*x*x + a*x;
        else if(i==1) //coeffs[1]
            return (a+2)*x*x*x - (a+3)*x*x + 1;
        else if(i==2) //coeffs[2]
            return -(a+2)*x*x*x + (2*a+3)*x*x - a*x;
        else if(i==3) //coeffs[3]
            return a*x*x-a*x*x*x;
        else
            return 0.0;
    };

    //左上角取整
    int stemp_x = floor(baseline_x);
    int stemp_y = floor(baseline_y);

    double delta_x = baseline_x - stemp_x;
    double delta_y = baseline_y - stemp_y;

    Mat xWeight(4,1,CV_64FC1);
    Mat yWeight(1,4,CV_64FC1);

    for(int i=0; i<4; i++){
        xWeight.at<double>(i,0) = getWeight(i,delta_x);
        yWeight.at<double>(0,i) = getWeight(i,delta_y);
    }

    //计算参考点附近十六个点矩阵,矩阵为参考点四舍五入的左2、右2、上2、下2范围
    int x_round = round(baseline_x+0.5);
    int y_round = round(baseline_y+0.5);
    Mat Mat16_ = input(Range(y_round-2,y_round+2),Range(x_round-2,x_round+2));

    Mat Mat16_b(4,4,CV_64FC1);  //分离通道各自计算
    Mat Mat16_g(4,4,CV_64FC1);
    Mat Mat16_r(4,4,CV_64FC1);
    Mat m16[3] = {Mat16_b,Mat16_g,Mat16_r};
    cv::split(Mat16_,m16);
    Mat result_b = yWeight*Mat16_b*xWeight;
    Mat result_g = yWeight*Mat16_g*xWeight;
    Mat result_r = yWeight*Mat16_r*xWeight;
    vector<double>result_array = {result_b.at<double>(0,0),result_g.at<double>(0,0),result_r.at<double>(0,0)};
    return result_array;
}

Mat getTargetMatrix(Mat& mSrc, int target_width, int target_height){
    //填充
    int padSize = 2;
    Mat mPad;
    copyMakeBorder(mSrc,mPad,padSize,padSize,padSize,padSize,BORDER_REPLICATE);
    Mat mResult(target_height,target_width,CV_64FC3); //三通道
    double scale_x = ((double)mSrc.cols/(double)target_width);
    double scale_y = ((double)mSrc.rows/(double)target_height);
    for(int i=0; i<target_height; i++){
        double y_temp = (i+0.5) * scale_y + 1.5;
        for(int j=0; j<target_width; j++){
            double x_temp = (j+0.5) * scale_x + 1.5;
            //改变接收逻辑
            mResult.at<Vec3d>(i,j)[0] = getObjectPixel(mPad,x_temp,y_temp)[0];
            mResult.at<Vec3d>(i,j)[1] = getObjectPixel(mPad,x_temp,y_temp)[1];
            mResult.at<Vec3d>(i,j)[2] = getObjectPixel(mPad,x_temp,y_temp)[2];
        }
    }
    return mResult;
}
int main(){
    Mat rawPic = imread("C:\\Users\\24364\\C_git\\opencv_test\\jLena.jpg",1);
    imshow("rawPic",rawPic);

    resize(rawPic,rawPic,Size(256,256),0,0); //防止计算量太大编译太慢，先缩小一半再计算

    int padSize = 200;//仅填充图结果
    Mat padPic;
    copyMakeBorder(rawPic,padPic,padSize,padSize,padSize,padSize,BORDER_REPLICATE);
    imshow("padPic",padPic);

    //插值结果，结果应该和原图大小一致
    rawPic.convertTo(rawPic,CV_64FC3);
    Mat test = getTargetMatrix(rawPic,512,512);
    test.convertTo(test,CV_8UC3);
    imshow("test",test);

    cout<<"Done";
    waitKey(0);
    destroyAllWindows();
    return 0;
}

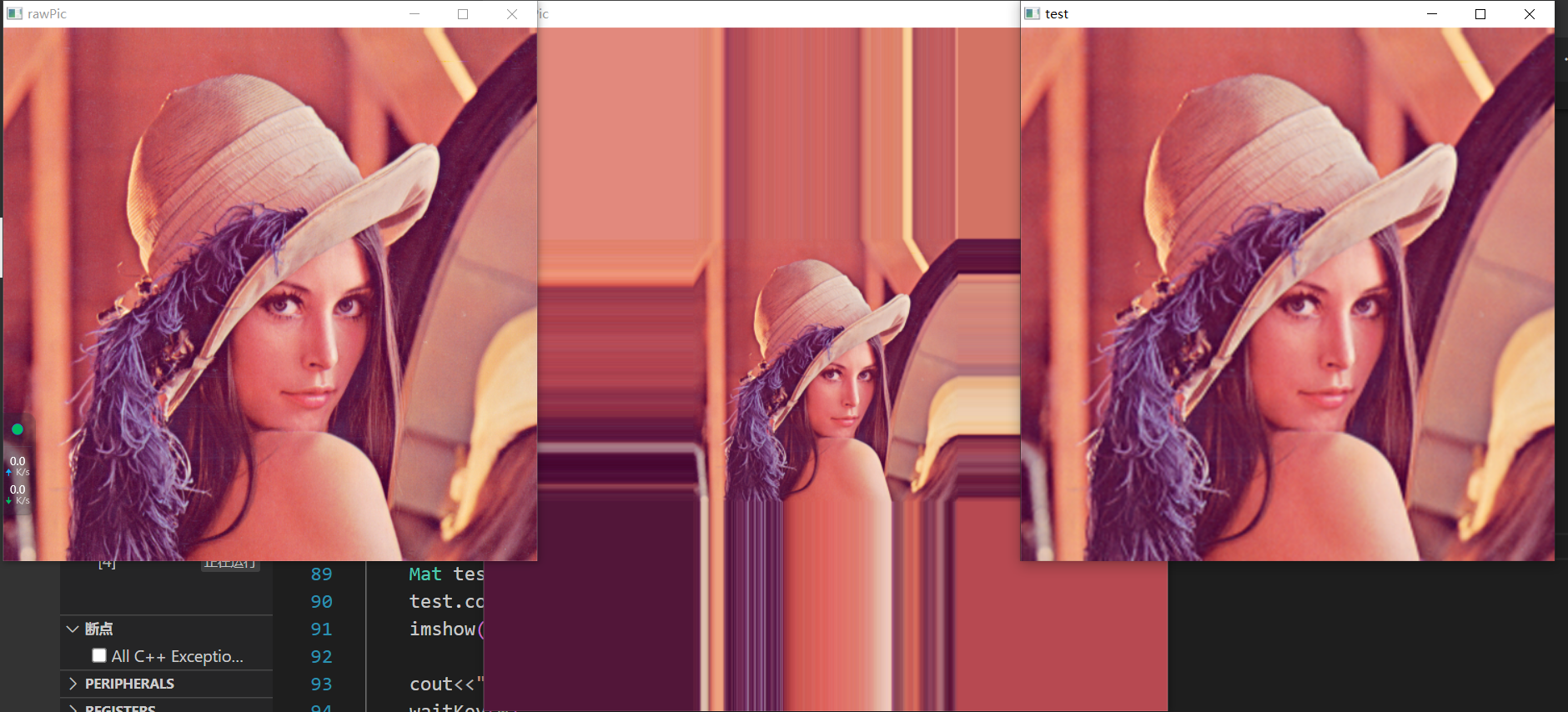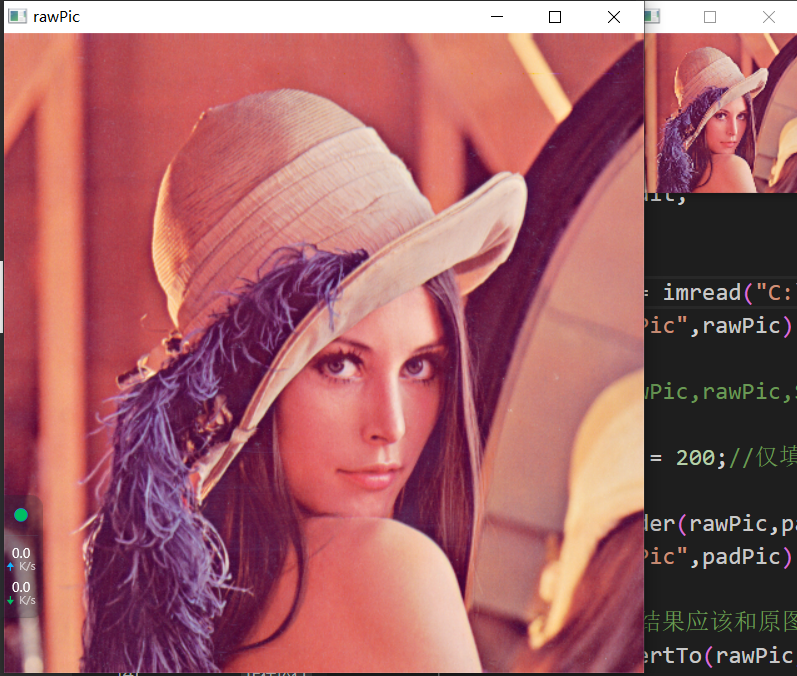
效果：图片双三次插值效果可以看到，中间的图是左侧的图直接使用邻近值边值填充的效果，造成边缘的拉伸；最右边是经过双三次插值的效果，比原图略微模糊，成功实现图的放大(这里为了减少双三次的计算量，先resize了一半再恢复原图)；再者，我们几乎没有讨论过图的缩小行为，这是因为OpenCV很少主动使用双三次插值进行缩小，但缩小本身也就一种下采样，也是能实现效果嘚，将512下采样成128大小如图：双三次插值效果缩小图片

使用像素区域关系重采样INTER_AREA

正如上文所述，OpenCV通常不会使用双三次插值进行图像缩小，而是推荐使用INTER_AREA，OpenCV仅说明其“根据像素区域关系重采样”得到结果，没有具体描述原理，好在还是找到了吃螃蟹的人，参考Aaron Dong的这篇分享OpenCV里的INTER_AREA究竟是在做啥？能比较清楚，以下均为原文摘录。

INTER_AREA时机

使用INTER_LINEAR或者INTER_LINEAR_EXACT(双线性插值的高精度版本)：当长宽缩小均为两倍、且图像通道不为2，那么实际上还是调用INTER_AREA方法；
使用INTER_AREA时，对于宽和高，如果执行的是放大操作，那么实际上调用的是INTER_LINEAR；

可见指定INTER_AREA，也不一定是调用INTER_AREA方法，不指定INTER_AREA，也未必不是INTER_AREA；

INTER_AREA缩小

INTER_AREA重采样原理，举例：

当宽和高均缩小三倍时，会在源矩阵构造3×3的Block，这个Block的平均像素，就是目标图像的新像素值；

当缩小倍数不是整数时，仍然遵循这种计算方法。

INTER_AREA放大

实际上调用的是“特殊的双线性插值INTER_LINEAR”，这个特殊性OpenCV系统已经实现，就是调用INTER_LINEAR；

使用上节双线性插值代码可以发现，大部分计算都是和直接调用INTER_LINEAR是相近的，但是当数据是一维的[0,1]，resize成1×4矩阵，我的程序输出结果是[0, 0.25, 0.75, 1]，这就是普通双线性插值的思想；而调用resize的INTER_LINEAR，输出是[0.5, 0.5, 0.5, 0.5]，说明这种情况的双线性插值系数是被特殊指定的。

参考链接：