数据结构算法题目（六）：优先队列专题
优先队列
优先队列是相对于普通队列而言的，普通队列是一种FIFO结构，优先队列能够按照元素的优先级进行排序，使优先级高的元素先出队。C++提供了一种数据结构priority_queue来定义优先队列，可见其在数据结构和算法上是有用的，例如排序、数据压缩、prim/Dijstra优化算法等。
优先队列可以使用数组、链表、二叉堆实现，二叉堆的出队、入队复杂度是O(logn)，因此一般选择二叉堆作为优先队列底层实现，本文旨在记录手写一个二叉堆（大根堆、小根堆）实现优先队列底层基本操作，包含调整、构建二叉堆、排序、插入、删除等，在数据结构与算法(三)：查找与排序算法基本实现了前三种操作。
大小根堆（大小顶堆）
在堆排序文章基本描述了两种结构，为了给数组排序，通过i、2i+1、2i+2数组位置元素进行讨论，结构上是一种树的重构，大根堆是根结点>=子结点，小根堆是根结点<=子结点，增序排序使用大根堆，增序排序是小元素下滤的过程，最后留在根结点的是最大的元素，再与最后的小结点交换，继续递归下滤。降序排序则是大元素下滤的过程，留在根结点的是最小元素。排序实际上是不断排除最大/最小元素，故下滤；如果是插入新元素，就是上滤过程。上滤和下滤只是基本术语，只要明白大根堆就是大元素向上冒、小元素往下沉，小根堆反之罢了。
priority_queue底层支持大根堆和小根堆创建，这里先给出大小根堆手写代码，再介绍此数据结构的接口函数。
大根堆五种基本操作
其中调整、构建、排序参考C语言部分，基本没问题；插入、删除个人推导，《大概率》也没问题：
调整操作：数组nums，大小size，将i位置的结点上滤/下滤至合适位置；
1
2
3
4
5
6
7
8
9
10
11
12
13void AdjustMaxHeap(vector<int>& nums,int size,int i){ //数组、数组长度、调整起始结点
int largest = i;
int left = 2*i+1;
int right = 2*i+2;
if(left<size&&nums[left]>nums[largest])
largest = left;
if(right<size&&nums[right]>nums[largest])
largest = right;
if(i!=largest){
swap(nums[i],nums[largest]);
AdjustMaxHeap(nums,size,largest);
}
}构建大顶堆 从最后一个非叶子节点开始往前递归，假设数组size，那么二叉堆的最后一个非叶子节点坐标一定是size/2-1，这是构建二叉堆最重要的结论。如果存在子结点大于其双亲结点，会上滤。
1
2
3
4
5void BuildMaxHeap(vector<int>&nums,int size){
for(int i=size/2-1; i>=0; i--){
AdjustMaxHeap(nums,size,i);
}
}排序算法：每次上滤和下滤结束最大的元素都在根结点，然后交换它和最后一个结点，继续下滤构建大顶堆即可以得到增序的输出：
1
2
3
4
5
6
7void Sort_MaxHeap(vector<int>&nums, int size){ //确保nums符合最大堆结构，否则先调用最大堆构造
//BuildMaxHeap(nums,size);
for(int i=size-1; i>0; i--){
swap(nums[i],nums[0]);
AdjustMaxHeap(nums,i,0); //注意i具有双层含义，既是坐标，也是范围
}
}插入操作：注意想想我们为什么要插入操作，向一个排序好的数组插入不影响顺序？这是错误的理解，大顶堆的插入指的是向一个大顶堆插入元素，不会影响它大顶堆的性质。因此构建完大顶堆，使用插入后也可以正常排序。
当然另一种取巧的方法是每次向数组插入后，再去构建大顶堆，就不用记这段代码了。还是给出：
两个重要结论：最后一个非叶子结点是size/2-1；结点的父节点是(i+1)/2-1；
1
2
3
4
5
6
7
8
9
10
11void Push_MaxHeap(vector<int>&nums,int elem){
nums.push_back(elem);
int cur= nums.size()-1; //两个含义：最后元素的坐标、插入前的数组大小
while((cur+1)/2-1>= 0){ //插入后的最后一个非叶子结点是size/2-1，即(cur+1)/2-1；
int i= (cur+1)/2-1;
if(nums[i]>nums[cur]) //父节点大，不用再交换
break;
swap(nums[i],nums[cur]); //交换到父节点位置
cur = i; //找父节点的父节点
}
}删除操作：查找删除某个元素意义不大，删除操作只针对删除根结点，因为它代表高优先的元素。直接使用最后元素覆盖，resize丢弃空间，然后下滤即可：
1
2
3
4
5
6
7int Pop_MaxHeap(vector<int>&nums){
int result = nums[0];
nums[0] = nums[nums.size()-1]; //覆盖根结点
nums.resize(nums.size()-1); //丢弃末尾空间
AdjustMaxHeap(nums,nums.size(),0); //下滤
return result;
}
小根堆五种基本操作
原理一致，修改上下滤逻辑即可： 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52//最小堆调整函数
void AdjustMinHeap(vector<int>& nums,int size,int i){
int smallest = i;
int left = 2*i+1;
int right = 2*i+2;
if(left<size&&nums[left]<nums[smallest]) //子结点小于双亲结点
smallest = left;
if(right<size&&nums[right]<nums[smallest]) //子结点小于双亲结点
smallest = right;
if(i!=smallest){ //小于就交换
swap(nums[i],nums[smallest]);
AdjustMinHeap(nums,size,smallest); //重复检查该子结点是否仍要上滤
}
}
//建立最小堆
void BuildMinHeap(vector<int>& nums,int size){
for(int i=size/2-1; i>=0; i--){
AdjustMinHeap(nums,size,i);
}
}
//最小堆排序
void Sort_MinHeap(vector<int>& nums,int size){
//BuildMinHeap(nums,nums.size());
for(int i=size-1; i>0; i--){
swap(nums[0],nums[i]);
AdjustMinHeap(nums,i,0);
}
}
//最小堆的插入
void Push_MinHeap(vector<int>& nums,int elem){
nums.push_back(elem);
int cur = nums.size()-1;
while((cur+1)/2-1 >= 0){ //父节点 = size/2-1
int i = (cur+1)/2-1;
if(nums[i]<nums[cur]) //父节点较小，停止上滤
break;
swap(nums[i],nums[cur]);
cur = i;
}
}
//最小堆返回并且弹出根结点
int Pop_MinHeap(vector<int>& nums){
int result = nums[0]; //记录
nums[0] = nums[nums.size()-1];
nums.resize(nums.size()-1); //丢弃空间
AdjustMinHeap(nums,nums.size(),0); //新结点要下滤
return result;
}
priority_queue
定义与比较
priority_queue不是一种全新的数据结构，在STL中它是一种基于vector的容器适配器，还有另一种底层是通过deque，这里记录最常用的vector，定义一个priority_queue需要在第二个参数指明它的底层，第三个参数指明比较规则：
1
2
3
4
5
6
7
8
priority_queue<int,vector<int>,less<int>> pq; //int类型，基于vector，大顶堆
priority_queue<int>pq; //大顶堆默认写法：默认vector容器和less
priority_queue<pair<int,int>>pq; //pair类型按照第一个值大小，建立大顶堆
//小顶堆需要指明容器和比较函数
priority_queue<int,vector<int>,greater<int>> pq;
如果需要定义自己数据结构的优先队列，并且自定义比较规则，通过仿函数可以实现：
！！！！！注意：如果仿函数从小到大排序，则认为小元素是低优先级，因此堆顶top()是最大元素！！！！！
1
2
3
4
5
6
7struct myCompare{
bool operator()(const pair<int,int>&p1, const pair<int,int>&p2){
return p1.second < p2.second; //对应一个大根堆，改成>，才是小根堆
}
};
priority_queue<pair<int,int>,vector<pair<int,int>>,myCompare>pq;
基本操作
同栈类似： 1
2
3
4
5
6push(elem); //元素入队
emplace(elem); //元素入队，区别就是emplace_back和push_back的区别，例如原地构造。
pop(); //根结点出队
top(); //根结点
size(); //堆中元素
empty(); //空
小结
优先队列用处：以O(logn)的时间复杂度代价完成插入和删除，以O(1)时间复杂度代价取出高优先级元素。
堆排序：利用优先队列，不断取出最大值、最小值实现排序，每次处理都会得到一个最值，n个数的时间复杂度是O(nlogn);
二叉堆结构的分析方法类似二叉树，但是其底层是数组存储而不是二叉树。
拓展
算法题中需要局部最大值，需要一些类似的数据结构不断维护这样的高优先级元素，目前接触到的有：
set/multiset/map/multimap：即红黑树，通过begin()、rbegin()取出最高优先级、最低优先级元素；
优先队列：刚刚说完；
单调队列/单调栈/双端队列：需要智慧和灵性。
其他偏向更深层业务逻辑的：跳表、ST表、线段树。
优先队列算法题目
1. 滑动窗口最大值
给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
example:输入：nums = [1,3,-1,-3,5,3,6,7], k = 3 输出：[3,3,5,5,6,7]
1 | class Solution { |
2. 前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
example:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
1 | struct myCompare{ |
3. 根据字符出现频率排序
给定一个字符串 s ，根据字符出现的 频率 对其进行 降序排序 。一个字符出现的 频率 是它出现在字符串中的次数。
返回 已排序的字符串 。如果有多个答案，返回其中任何一个。
示例 1:
example:输入: s = "tree"
输出: "eert"
解释: 'e'出现两次，'r'和't'都只出现一次。
因此'e'必须出现在'r'和't'之前。此外，"eetr"也是一个有效的答案。
哈希表统计频率，优先队列求高频，输出时根据频率输出字符即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26struct myCompare{
bool operator()(const pair<char,int>&p1,const pair<char,int>&p2){
return p1.second < p2.second;
}
};
class Solution {
public:
string result;
string frequencySort(string s) {
unordered_map<char,int>umap;
for(int i=0; i<s.size(); i++){
umap[s[i]]++;
}
priority_queue<pair<char,int>,vector<pair<char,int>>,myCompare>pq;
for(auto &i : umap){
pq.push(i);
}
while(!pq.empty()){
int num = pq.top().second;
while(num--)
result.push_back(pq.top().first);
pq.pop();
}
return result;
}
};
4. 最接近原点的 K 个点
给定一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点，并且是一个整数 k ，返回离原点 (0,0) 最近的 k 个点。
example:输入：points = [[1,3],[-2,2]], k = 1
输出：[[-2,2]]
解释：
(1, 3) 和原点之间的距离为 sqrt(10)，
(-2, 2) 和原点之间的距离为 sqrt(8)，
由于 sqrt(8) < sqrt(10)，(-2, 2) 离原点更近。
我们只需要距离原点最近的 K = 1 个点，所以答案就是 [[-2,2]]。
最近距离，应该使用小顶堆。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int compu_distance(vector<int>& vp){ //计算欧几里得距离
return (int)pow(vp[0],2) + (int)pow(vp[1],2);
}
vector<vector<int>>result;
vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>pq;//小顶堆
for(int i=0; i<points.size(); i++){
int distance = compu_distance(points[i]);
pq.push(make_pair(distance,i)); //插入，默认排序first
}
while(k--){ //统计结果
result.push_back(points[pq.top().second]);
pq.pop();
}
return result;
}
};
5. 丑数Ⅱ
给你一个整数 n ，请你找出并返回第 n 个 丑数 。
丑数 就是质因子只包含 2、3 和 5 的正整数。
example:
输入：n = 10
输出：12
解释：[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。
问题分析：丑数的难点在于如何确定第n个丑数的大小范围，保守的估计是第n个丑数必然小于5^n，但是复杂度过大无法这样遍历，因此这里采取贪心+优先队列的算法，每次将因子放在优先队列，将最小堆的元素（最小值）压入并且计数，注意因子元素可能重叠，在弹出时也要带走一系列相同值。
1 | class Solution { |
时间复杂度：来自最小堆的排序，O(nlogn)
空间复杂度：每次最多压入3个，和n是线性关系，O(n)。
为了应对其他题目对丑数的判断，记录其判断函数应该是：
1
2
3
4
5
6
7
8
9bool isUgly(int num){
while(num%2==0)
num /= 2;
while(num%3==0)
num /= 3;
while(num%5==0)
num /= 5;
return num==1;
}
对顶堆题目
除了维护最大值、最小值，也有的应用场景使用两个优先队列，解决中位数问题。
维护中位数最直观就是两个数组排序，一个数组放小值，另一个放大值，取其中一端或者其平均值，而难点在于两个数组的元素是可能发生转化的，因为随着添加元素大小不同，两个数组的边缘值可能加入另一个数组。优先队列能够帮助解决排序问题，但还需要更复杂的转化逻辑。
这里引入一种数据结构——对顶堆，对转化逻辑很有帮助,如图：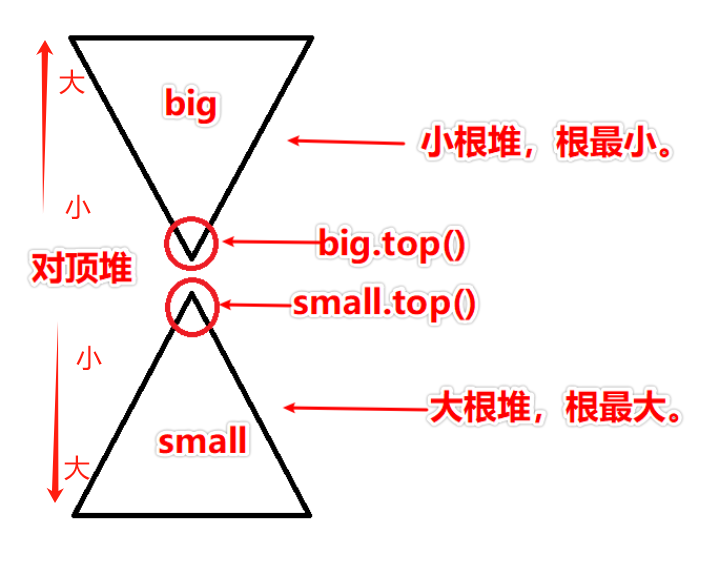 
除了大小关系，还需要保证双方size差别不超过1，否则需要进行元素转化（风险对冲），要么下方top插入上方，要么上方top插入下方。见例题。
1. 数据流的中位数(Hard题)
中位数是有序整数列表中的中间值。如果列表的大小是偶数，则没有中间值，中位数是两个中间值的平均值。
例如 arr = [2,3,4] 的中位数是 3 。
例如 arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。
实现 MedianFinder 类:
MedianFinder() 初始化 MedianFinder 对象。
void addNum(int num) 将数据流中的整数 num 添加到数据结构中。
double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10-5 以内的答案将被接受。
对顶堆维护中位数过程：第一个元素插入下方作为baseline，第二个元素如果大于baseline，就进入上方的堆，假设再来两个大于baseline元素，则除了插入上方的堆，还会触发风险对冲，上方top()进入下方堆（可能成为新的baseline），维持大小size平衡。模拟这个过程总会发现：当插入为奇数，两个堆较大的一方的top恰好就是中位数，为偶数时就是双方的平均值。
代码： 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class MedianFinder {
public:
priority_queue<int,vector<int>,greater<int>>upheap; //最小堆
priority_queue<int>downheap; //最大堆
int size; //记录插入次数，方便判断奇偶
MedianFinder() {
size = 0;
}
void addNum(int num) {
size++;
if(downheap.empty()||num<=downheap.top()) //开始时插入下面最大堆
downheap.push(num);
else //大于baseline，插入最小堆
upheap.push(num);
//风险对冲
if(downheap.size()+1<upheap.size()){ //size不均衡，上面元素转化下面
downheap.push(upheap.top());
upheap.pop();
}
if(upheap.size()+1<downheap.size()){ //size不均衡2，下面转上面
upheap.push(downheap.top());
downheap.pop();
}
}
double findMedian() { //计数中位数
if(size%2==1){ //奇数
if(downheap.size()>upheap.size())
return downheap.top();
else
return upheap.top();
}
else //偶数
return (double)(downheap.top()+upheap.top())/2;
}
};
时间复杂度：插入n次，O(nlogn)
空间复杂度：插入n个数，O(n)
2. 滑动窗口中位数(Hard题)
中位数是有序序列最中间的那个数。如果序列的长度是偶数，则没有最中间的数；此时中位数是最中间的两个数的平均数。
例如：
[2,3,4]，中位数是 3
[2,3]，中位数是 (2 + 3) / 2 = 2.5
给你一个数组 nums，有一个长度为 k 的窗口从最左端滑动到最右端。窗口中有 k
个数，每次窗口向右移动 1
位。你的任务是找出每次窗口移动后得到的新窗口中元素的中位数，并输出由它们组成的数组。
example:输入nums = [1,3,-1,-3,5,3,6,7]， k = 3。 输出：[1,-1,-1,3,5,6]
解析：
窗口位置 中位数
--------------- -----
[1 3 -1] -3 5 3 6 7 1
1 [3 -1 -3] 5 3 6 7 -1
1 3 [-1 -3 5] 3 6 7 -1
1 3 -1 [-3 5 3] 6 7 3
1 3 -1 -3 [5 3 6] 7 5
1 3 -1 -3 5 [3 6 7] 6
因此，返回该滑动窗口的中位数数组 [1,-1,-1,3,5,6]。
问题分析：进阶的对顶堆求中位数问题，这道Hard题代码难度还是比较高。首先仍然采用对顶堆的数据结构，但是除了中位数要出队，过期的窗口元素也需要出队，然而C++的优先队列并不支持非堆顶元素出队，因此只能采用延迟删除的策略，当元素过期时，使用哈希表标注该元素，而且认为该值逻辑上删除，size-1，等到该值出现在堆顶时再将其直接删除。
因此现在使得size失衡的来源有两个：其一是元素过期，导致size-1;其二是插入元素时风险对冲，size值不能失衡（中位数原理），因此维护了一个balance字段记录，当下方最大堆的元素失效，balance--，当上方最大堆元素失效，balance++，当下方插入新元素，balance++，上方插入新元素，balance--，可见balance的含义就是下方最大堆size相比于上方堆size的增量，取值只可能是0、±2。
此外，与上一题不同的是，由于k是确定的，开始时不必默写一套上面算法查找0——k-1元素的中位数，只需要放k个在最大堆，再从堆顶取k/2（不含）放在最小堆；最大堆的元素至少比最小堆多一个，因此中位数只可能是来自下方最大堆。只需要判断k奇偶即可。
代码： 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72class Solution {
public:
vector<double> medianSlidingWindow(vector<int>& nums, int k) {
priority_queue<int,vector<int>,greater<int>>upheap; //上方最小堆
priority_queue<int>downheap; //下方最大堆
vector<double> result;
unordered_map<int,int>umap; //记录过期元素
//寻找0——k-1的中位数
for(int i=0; i<k; i++){ //放k个最大堆
downheap.push(nums[i]);
}
for(int i=0; i<=k/2; i++){ //k/2个最大值转移最小堆
upheap.push(downheap.top());
downheap.pop();
}
if(k%2==1)
result.push_back(downheap.top()); //第一个中位数
else
result.push_back(((double)upheap.top()+(double)downheap.top())/2); //第一个中位数
//处理滑动窗口
for(int i=k; i<nums.size(); i++){
int balance = 0; //size损失量，负数来自下堆，正数来自上堆
//记录过期元素、计算balance、检查栈顶是否还债
umap[nums[i-k]]++; //窗口过期元素
if(nums[i-k]<=downheap.top()) //过期元素是最小堆的
balance--; //downheap的size逻辑损失1，欠债
else
balance++; //upheap的size逻辑损失1，欠债
while(!downheap.empty()&&umap[downheap.top()]>0){ //检查堆顶是否欠债
umap[downheap.top()]--;
downheap.pop(); //欠债还债
}
while(!upheap.empty()&&umap[upheap.top()]>0){
umap[upheap.top()]--;
upheap.pop(); //欠债还债
}
//开始插入新滑动窗口元素
if(nums[i]<=downheap.top()){ //小于baseline
downheap.push(nums[i]);
balance++;
}
else{ //大于baseline
upheap.push(nums[i]);
balance--;
}
//balance触发风险对冲：必须保证因为过期、插入等操作带来的size平衡
if(balance==2){ //失效来自上堆、插入在下堆
upheap.push(downheap.top()); //下堆转上
downheap.pop();
}
if(balance==-2){ //失效来自下堆、插入在上堆
downheap.push(upheap.top());
upheap.pop(); //上转下
}
//转移后可能出现新堆顶，要保证堆顶不是欠债元素，因为已经是失效元素。
while(!downheap.empty()&&umap[downheap.top()]>0){ //还债
umap[downheap.top()]--;
downheap.pop();
}
while(!upheap.empty()&&umap[upheap.top()]>0){ //还债
umap[upheap.top()]--;
upheap.pop();
}
//记录结果
if(k%2==1)
result.push_back(uphead.top());
else
result.push_back(((double)upheap.top()+(double)downheap.top())/2);
}
return result;
}
};