以下所有内容编排按照Carl开源的算法攻略进行，感谢博主悉心的内容挑选和顺序编排。编程语言为C++；

回溯算法篇

回溯算法是一种经典的算法，旨在让计算机穷尽各种可能，广泛用于处理组合问题、子集问题、排列问题等等，回溯算法可以被设计得很精妙，开始时难以理解是不可避免的，关键还是从基本题目入手，逐渐体会其中原理，Carl以及其他算法博客已经把规律总结很好，本篇文章只是记录而并非教程；虽然回溯算法很巧妙，但是代码写法一般比较固化，回溯算法普遍使用的算法模板如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
travel(){
    if(//每次递归结束的条件) //深度控制，不可能无限向下递归
        .....
        return；
    //递归套循环是很常见的事情，递归控制搜索的深度，循环控制单次处理时的广度 
    for(){
        //决策
        //标记
        ......
        //travel
        //取消决策
        //取消标记
        ......
    }
    ......
}
有人把递归形容成遍历决策树的过程，每次的决策、标记，实际上就是上一层结点向下一层深入递归，取消决策、标记就是所谓的回溯，重新回到上一层进行决策；通过这样遍历完所有决策树过程，就是解决问题的出路，也是代码的基本框架。

1. 组合数

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

example:输入：n = 4, k = 2 输出： [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4],]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int>temp; //存储单次递归结果
    vector<vector<int>>result;  //存储最后结果
    void travel(int n,int k,int start){  //start用于控制每次递归开始的数字
        if(temp.size()==k){  //深度控制，如果temp是k个了，就输入到结果数组
            result.push_back(temp);
            return;
        }
        for(int i=start;i<=n;i++){ 
            temp.push_back(i);   //决策
            travel(n,k,i+1); //i+1作为start，说明取数不要重复，也不要回头
            temp.pop_back(); //取消决策
        }
    }
    vector<vector<int>> combine(int n, int k) {
        travel(n,k,1);
        return result;
    }
};

2. 组合总和III

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

  • 所有数字都是正整数。

  • 解集不能包含重复的组合。

example:输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]

注意递归的逻辑，每次temp入栈result后，都会清空一位给新元素，继续递归执行，并不是说每次都清空temp再重新统计。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int>temp;
    vector<vector<int>>result;
    void travel(int k,int n,int start){
        if(temp.size()==k&&accumulate(temp.begin(),temp.end(),0)==n){  //个数为k，和为n
            result.push_back(temp);
            return;
        }
        for(int i=start;i<=9;i++){  //从start开始循环
            temp.push_back(i); //决策压栈
            travel(k,n,i+1);
            temp.pop_back();  //弹栈取消决策
        }
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        travel(k,n,1);
        return result;
    }
};

3. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

电话数字与字母映射： 

1
2
3
4
5
6
7
8
9
10
11
12
const string str[10]={
    "",      //0，只是为了对齐
    "",      //1
    "abc",   //2
    "def",   //3
    "ghi",   //4
    "jkl",   //5
    "mno" ,  //6
    "pqrs",  //7
    "tuv",   //8  
    "wxyz"   //9
};

example:输入：digits = "23" 输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

比起组合数，这是一个二维的题目，需要解析出数字数组对应的字母，再使用循环递归遍历； 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    const string str[10]={
    "",      //0，只是为了对齐
    "",      //1
    "abc",   //2
    "def",   //3
    "ghi",   //4
    "jkl",   //5
    "mno" ,  //6
    "pqrs",  //7
    "tuv",   //8  
    "wxyz"   //9
    };
    string temp;
    vector<string> result;
    void travel(string digits,int id){
        if(temp.size()==digits.size()){
            result.push_back(temp);
            return;  //记住返回，否则id会越界，或使用if(id>=digits.size()) return，这里就可以去除
        }
        int index = digits[id]-'0';  //digits[id]="2"，index=2，id=0
        for(int i = 0;i<str[index].size();i++){ //索引到对应的str[index]字符，2就找2的对应字符abc
            temp.push_back(str[index][i]);  //压栈
            travel(digits,id+1);  //不是index+1，id是digital下标，index是对应元素
            temp.pop_back();
        }
    }
    vector<string> letterCombinations(string digits) {
        if(digits.size()==0)
            return {};
        travel(digits,0); //从digits的0下标开始解析
        return result;
    }
};

4. 组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

example:输入：candidates = [2,3,6,7], target = 7 输出：[[2,2,3],[7]] 解释： 2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选， 7 = 7 。 仅有这两种组合。

关键的地方是两个细节的配合，首先i从start开始，其次是travel(candidates,target,i)，意味着下一次递归仍然可以使用当前数字，例如2，3，4，5，能重复使用2，2，3这样的组合，但是一旦i++,就不可能产生3，2，2这种重复组合，因此排除了因为回头产生重复的可能性。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int>temp;
    vector<vector<int>>result;
    void travel(vector<int>&candidates, int target, int start){
        int sum = accumulate(temp.begin(),temp.end(),0);
        if(sum==target){  //和为target，入栈
            result.push_back(temp);
            return;
        }
        if(sum>target) //大于target，已无可能
            return;
        for(int i=start;i<candidates.size();i++){
            temp.push_back(candidates[i]);
            travel(candidates,target,i);
            temp.pop_back();
        }
    }
    
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        travel(candidates,target,0);
        return result;
    }
};

5. 组合总和II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

example:输入:candidates = [10,1,2,7,6,1,5], target = 8, 输出: [ [1,1,6], [1,2,5], [1,7], [2,6]]

比起上题，这题变化的条件是：candidates可能出现重复的元素，而且每个数字只能用一次，但仍要保证没有重复组合；

由于重复元素的存在，尽管"不回头"仍然可能产生相同的组合，这里去重问题一般可能只能通过数据结构去去除，但这里有一种方法，使用sort排序以及i>start&&candidates[i-1]==candidates[i]进行判断，这个判断确保每次循环时遇到重复元素，只有start元素会被压栈，多个重复元素由递归实现，for不会同时压入两个相同的元素；如果是判断条件是candidates[i+1]==candidates[i]会直接跳过所有重复元素，且只保留i+1的重复元素，导致start无法通过递归累积，遗漏了多个相同元素的结果。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<int>temp;
    vector<vector<int>>result;
    void travel(vector<int>& candidates_sort, int target,int start){
        int sum = accumulate(temp.begin(),temp.end(),0);
        if(sum>target)
            return;
        if(sum==target){
            result.push_back(temp);
            return;
        }
        for(int i=start; i<candidates_sort.size(); i++){
            if(i>start&&candidates_sort[i]==candidates_sort[i-1])  //去重
                continue;
            temp.push_back(candidates_sort[i]);
            travel(candidates_sort,target,i+1);
            temp.pop_back();
        }
    }

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        sort(candidates.begin(),candidates.end());  //排序
        travel(candidates,target,0);
        return result;
    }
};

6. 分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是回文串。返回 s 所有可能的分割方案。

example:输入：s = "aab" 输出：[["a","a","b"],["aa","b"]]

递归去分割一个字符s，回文字符才会入栈且递归继续分割，否则会跳过；代码逻辑更清晰： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    vector<string>temp;
    vector<vector<string>>result;
    bool is_pdrome(string& sub_str){  //判断字串是否回文
        int left = 0;
        int right = sub_str.size()-1;
        while(sub_str[left]==sub_str[right]){
            left++;
            right--;
            if(left>=right)
                return true;
        }
        return false;
    }
    
    void travel(string& s,int start){
        if(start>=s.size()){   //递归越界，说明递归已经划分完一个s
            result.push_back(temp);
            return;
        }
        for(int i=start;i<s.size();i++){ 
            string sub_str = s.substr(start,i-start+1); //从start开始划分i-start个
            if(is_pdrome(sub_str)==true){   //回文才会执行递归
                temp.push_back(sub_str);
                travel(s,i+1);
                temp.pop_back();
            }
            else
                continue; //如app，非回文，切换i，切换切割方法，不能return
        }
    }
    
    vector<vector<string>> partition(string s) {
        travel(s,0);
        return result;
    }
};

7. 复原 IP 地址

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

  • 例如："0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。

给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

感觉除了递归，字符串分割也是难点之一，需要考虑的细节比较多，例如如何判断字符有效性、分割完成如何有序添加分隔点，最大一个特点是加完分隔符后，IP地址最后一节的数字需要额外处理，因为无法和分隔符放在一起；总体而言实现是自由的。

我的方案： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<exception>
class Solution {
public:
    string temp;
    vector<string>result;
    int dotnum =0;
    bool is_Valid(string& sub_str){ //判断分割子串是否有效
        int s2i_str;
        try{
            s2i_str = stoi(sub_str);  //防止substr越界
        }
        catch(exception &e){
            return false;
        }
        if(s2i_str==0&&sub_str.size()==1)  //只有一个0是有效，多个0无效
            return true;
        if((s2i_str>0&&s2i_str<=255)&&sub_str[0]!='0') //1~255有效，以0开始无效
            return true;
        return false;
    }

    void travel(string& s, int start){
        string last_sub = s.substr(start); 
        if((dotnum == 3&&is_Valid(last_sub))){ //dotnum==3代表分割点完成，要开始处理最后一节
            temp.append(last_sub); //最后一节合法加入
            result.push_back(temp); 
            temp.erase(temp.end()-last_sub.size(),temp.end()); //擦除，最后一节还会有其他结果（这是一种手动回溯）
            return;
        }
        for(int i =start; i<s.size(); i++){
            string sub_str = s.substr(start,i-start+1);
            if(is_Valid(sub_str)){ //合法
                temp.append(sub_str); //入栈
                if(dotnum<3){  //少点
                    temp.push_back('.'); //加点
                    dotnum++;
                    travel(s,i+1);
                    temp.pop_back();
                    dotnum--;
                }
                temp.erase(temp.end()-(i-start+1),temp.end()); //回溯
            }
            else //不用continue，因为已经分割出非法字符（例如0开头、大于255），后面怎么分该位置都是非法的
                break;
        }
    }
    vector<string> restoreIpAddresses(string& s) {
        travel(s,0);
        return result;
    }
};

8. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的 子集 （幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

example:输入：nums = [1,2,3] 输出：[[],[1],[2],[3],[1,2],[1,2,3],[2,2],[2,3]]

问题分析：因为数组不存在重复元素，不回头查找本身就不会产生重复子集，因此本质就是找各种的数组组合，关键是要找到终止条件，什么时候停止搜索，从数学而言一个数组的子集数目是确定的，子集数目=其组合数求和，但是这里没必要计算其组合数，直接使用数组是否存在即可，因为循环控制了数组遍历的广度，进而也控制了参与递归的变量数目，所有元素返回，递归也就结束了，所以也能变相控制深度。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int>temp;
    vector<vector<int>>result;
    void travel(vector<int>& nums,int start){
        if(&temp!=nullptr){  //不为空就入栈
            result.push_back(temp);  //注意不能return，因为这个数组还要压栈
        }
        for(int i=start; i<nums.size(); i++){
            temp.push_back(nums[i]);
            travel(nums,i+1);  
            temp.pop_back();
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        travel(nums,0);
        return result;
    }
};

9. 子集 II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的 子集 （幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

example:输入：nums = [1,2,2] 输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

和第五题组合总和II的做法是一样的，数组出现了重复元素，不回头不能完全排除重复的子集，因此需要进行排序和跳过，for循环不能引入多个相同字符，重复的字符只能从递归引入，就保证相同的重复字符组合只出现一次。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    vector<int>temp;
    vector<vector<int>>result;
    void travel(vector<int>& nums,int start){
        if(&temp!=nullptr){
            result.push_back(temp);  //注意，不能return，找到一个还需要继续压栈
        }
        for(int i=start; i<nums.size(); i++){
            if(i>start && nums[i]==nums[i-1]) //必要操作，跳过循环的重复字符，只允许start是重复字符
                continue;
            temp.push_back(nums[i]);
            travel(nums,i+1);
            temp.pop_back();
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(),nums.end());  //小到大排序
        travel(nums,0);
        return result;
    }
};

10. 非递减子序列

给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。

example:输入: [4, 6, 7, 7] 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

题目分析：因为是子序列，因此不能通过大小排序来改变原来顺序，意味着重复的数组无法通过跳过相同元素的方式来排除，因此这里引入了哈希表结构，每次for循环都会初始化一个空的哈希表，并且检查这次for循环是否已经载入了重复元素，例如7，7如果是后面的7不会被引入，只有递归会产生重复元素，因此能够实现和原来排序并且continue相同的效果。

注意这个哈希表是针对广度而言，也即每次for循环都是新的一个哈希表，如果是深度控制的，则不能在travel递归函数中定义，要么通过类变量的方法，就像使用temp和result去记录递归结果，要么通过travel参数传递方法，每次递归都会将上一次的参数传到下一次递归去，见下一题的全排列。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int>temp;
    vector<vector<int>>result;
    void travel(vector<int>&nums,int start){
        if(temp.size()>1){
            result.push_back(temp);
        }
        unordered_set<int>record;   //局部变量哈希表控制广度，相当于sort去重，但是子序列无法用sort
        for(int i=start; i<nums.size(); i++){
            if(record.count(nums[i])!=0)  //没有重复
                continue;
            if(!temp.empty()&&nums[i]<temp.back())  //非递减
                continue;
            record.insert(nums[i]);
            temp.push_back(nums[i]);
            travel(nums,i+1);
            temp.pop_back();
        }
    }

    vector<vector<int>> findSubsequences(vector<int>& nums) {
        travel(nums,0);
        return result;
    }
};

11. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

example:输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

题目分析：全排列的问题就是回头遍历，回头的同时又要确保当前的元素在两次递归中不能被重复使用，因此要使用深度控制，方法就是定义一个类成员遍历，或者使用递归函数传参的方法，这里我使用的是前者；在12-全排列Ⅱ使用后者；

这当然不是最好的方法，因为哈希表实在是无奈之举，vector定义类变量时不能提前获知i的范围，因此不能未初始化大小直接使用used[i] =1这种语句，所以类成员变量只能使用哈希表这种随便插入查找的结构；其次每次递归返回都需要erase掉这个变量，因为进入其他for循环递归也会用到这个哈希表，而之前的非递减子序列问题每一层是广度控制，每一次递归都是新表，防止的是for引入重复元素，无需erase； 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int>temp;
    vector<vector<int>>result;
    unordered_set<int>used;  //放外面是深度控制，防止递归到重复元素
    void travel(vector<int>& nums){
        if(temp.size()==nums.size()){
            result.push_back(temp);
            return;
        }
        for(int i=0; i<nums.size();i++){
            if(used.find(i) != used.end())  //用过，跳过
                continue;
            temp.push_back(nums[i]);
            used.insert(i);    //标记
            travel(nums);  //递归的时候就不会递归到自己
            temp.pop_back();
            used.erase(i);  //取消标记
        }
    }

    vector<vector<int>> permute(vector<int>& nums) {
        travel(nums);
        return result;
    }
};

12. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

example:输入：nums = [1,1,2] 输出： [[1,1,2], [1,2,1], [2,1,1]]

问题分析：与上题相比，这里允许了nums包含重复元素，而且要求组合不能重复，所以这里回头时，除了要注意上题一样递归时不能选中自己以外（不能出现111、221），还不能选中和自己一样值的元素（111），因为终止条件只控制了数组大小。

因此在上题的基础上增加使用广度控制，全排列既可以使用之前重新排序的方法，跳过重复元素，也可以使用非递增子序列的哈希表的方法，后者只需要在上题代码做小小的改动：

方法一： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<int>temp;
    vector<vector<int>>result;
    unordered_set<int>usetdeep; //放外面是深度控制，防止递归到自己
    void travel(vector<int>nums){
        if(temp.size()==nums.size()){
            result.push_back(temp);
            return;
        }
        unordered_set<int>usetbroad;   //放里面的是广度控制，防止递归到和自己相同的元素
        for(int i=0; i<nums.size(); i++){
            if(usetbroad.count(nums[i])!=0)  //广度跳过相同元素
                continue;
            if(usetdeep.count(i)!=0)  //深度跳过自己
                continue;
            usetbroad.insert(nums[i]);
            temp.push_back(nums[i]);
            usetdeep.insert(i);
            travel(nums);
            temp.pop_back();
            usetdeep.erase(i);
        }
    }

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        travel(nums);
        return result;
    }
};

方法二：性能优化的方法，使用数组而不是哈希表结构，因此需要使用递归函数传参，并通过大小判断是否跳过重复元素，这种方法删去了注释部分，就是上题的答案，注释部分就是广度控制，这种方法有需要特别注意的地方如下。

比起组合和、子集等，这里新增了used[i-1]==0，代表只有i-1相同的值被使用了，才会被使用，例如数组[1,1,1]，第一次时i==0的1优先被选中，其used[0]=1，意味着递归时就可以使用第二个1了，因此元素的挑选顺序会按照原来的数组顺序；

假如没有这个条件，那么回头时会发现，只要相等的元素都会被去除，因此如果数组凑不齐大小，就不会出现输出；

神奇的地方是，这里改成used[i-1]==1一样能够通过测试，这时候就意味着i-1被使用的，会被跳过，因此上面就不会递归使用第二个1，而是第三个1，然而发现第二个1仍然不能使用，意味着从第一个1开始的递归分支是废的，同理第二个分支也是废的，for循环进入第三次，找到第三个1，然后第二个1、第一个1，才能找到正确组合。（这里看不懂可以对照卡哥的原文图片）

因此它们都能够正确索值，但是前者跳过0的方案剪枝效率更高，因此性能一般更好。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<int>temp;
    vector<vector<int>>result;
    void travel(vector<int>& nums , vector<int>& used){
        if(temp.size()==nums.size()){
            result.push_back(temp);
            return;
        }

        for(int i=0; i<nums.size();i++){
            if(i>0&&nums[i-1]==nums[i]&&used[i-1]==0)  //广度控制,used[i-1]==1亦可通过
                continue;  //跳过重复元素
            if(used[i]==1)
                continue;
            temp.push_back(nums[i]);
            used[i] =1;
            travel(nums,used);
            temp.pop_back();
            used[i] =0;
        }
    }

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        vector<int>used(nums.size());
        travel(nums,used);
        return result;
    }
};

13. 重新安排行程

给你一份航线列表 tickets ，其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。

所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。

例如，行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小，排序更靠前。

假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。

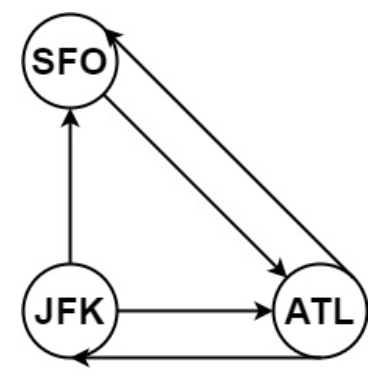
example:输入：tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]] 输出：["JFK","ATL","JFK","SFO","ATL","SFO"] 解释：另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"] ，但是它字典排序更大更靠后。 重新安排行程示意图

问题分析：

难度在于如何表达ticket路径的概念，这里采用一个unordered_map套map的结构，例如：{"JKF":{"MUC",1}}，其中"JKF"代表机票起点，"MUC"代表机票终点，数字代表这个起点到终点的重复机票数。这样ticket数组就被整合成了这个结构，例如["JKF","MUC"]、["JKF","LHR"]和["LHR","JKF"]就可以表示成{"JKF":{"MUC",1},{"LHR",1},"LHR":{"JKF",1}};

从JKF开始，就遍历键值JKF的哈希表项，因为使用的是map结构，因此首先索引到的肯定是LHR作为终点，此时递归切换遍历对象至LHR，遍历LHR的哈希表项；以此类推，递归的结束条件是完成规划地点数为票数+1，即可退出，因为这里只需要选出第一次的递归结果，因为map结构已经保证字符首字母是有序的，因此采用bool直接return，以及递归中return即可，如果需要保存所有结果，才使用数组和void类型使其回溯记录所有结果。

一些问题在题目一那篇文章也写过，即重复元素的计数一般考虑哈希表计数、或者multimap插入的方法，但是multimap删除会导致重复键值全部删除，即迭代器失效，因此这里采用的是unordered_map;

如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    //string temp;
    vector<string> result;
    bool travel(vector<vector<string>>& tickets,unordered_map<string,map<string,int>>&plan){
        if(result.size() == tickets.size()+1)   //字符串数目为票数+1，说明以及形成一次规划路线
            return true;
            string start = result.back(); //读取起点字符
            for(auto &pos:plan[start]){  //pos对应起始字符的机票
                if(pos.second>0){  //有机票
                    result.push_back(pos.first); //终点入栈
                    pos.second--;  //耗费机票
                    if(travel(tickets,plan)) //递归查找下一个起点，即以终点站为新起点
                        return true;  //形成完整路径才会return
                    result.pop_back(); //否则回溯继续查找
                    pos.second++;       //取消决策
                }
            }
        return false;
    }

    vector<string> findItinerary(vector<vector<string>>& tickets) {
        unordered_map<string,map<string,int>>plan;  
        for(auto pos:tickets){
            plan[pos[0]][pos[1]]++; //将机票数组转换成描述的结构
        }
        result.push_back("JFK"); //初始时起点入栈
        travel(tickets,plan);
        return result;
    }
};

贪心算法篇

目光短浅算法：为了得到全局最优解，先尝试每次达到局部最优解。

1. 分发饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

example: 输入: g = [1,2,3], s = [1,1] 输出: 1 解释: 你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。 虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。 所以你应该输出1。

贪心算法：两个思路

  1. 每次分发中，把大尺寸饼干分给大胃口的孩子，这个时候，过大胃口的孩子是吃不到饼干的，因此要遍历胃口（胃口吃不到也要循环）；

  2. 每次分发中，把小尺寸饼干分给小胃口的孩子；这时候，太小的尺寸的饼干是发不出去的，因此要遍历饼干（饼干发不出也要循环）；

总而言之，只需要排除把大饼干分发给小胃口孩子的情况。

思路一代码： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    static bool Mycmp(int left,int right){
        return left>right;
    }

    int findContentChildren(vector<int>& g, vector<int>& s) { //胃口数组g、饼干大小数组s
        sort(g.begin(),g.end(),Mycmp);
        sort(s.begin(),s.end(),Mycmp); //从大到小排序
        int i=0;
        int result=0;
        for(const auto&pos:g){ //遍历胃口
            if(i<s.size()&&pos<=s[i]){  //饼干未分完并且胃口小于饼干大小
                result++;  //分发成功+1
                i++;  //分下一块饼干
            }
        }
        return result;
    }
};

思路二代码： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(),g.end());  //胃口、饼干小到大排序
        sort(s.begin(),s.end());
        int result=0;
        int i=0;
        for(const auto&pos:s){ //遍历饼干
            if(i<g.size()&&pos>=g[i]){  //胃口没遍历完并且饼干大于胃口
                result++;
                i++;
            }
        }
        return result;
    }
};
细节问题是不能pos>=g[i]&&i<g.size()，这样会导致数组越界访问。

2. 摆动序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。 子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

example: 输入：nums = [1,17,5,10,13,15,10,5,16,8] 输出：7 解释：这个序列包含几个长度为 7 摆动序列。 其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8)

首先不要理解错题意：只是从任意序列中挑选出一个摆动序列，返回该序列的最大长度，并不要求挑选的字符串是连续的；因此只需要关注序列的峰和谷，排除那些连续上升，或者持平的点；假设刚开始1个点长度就是1，fast>0&&slow<=0表示快指针攀峰，慢指针未动或在上一个谷值，当fast遇到连续上升时，只要进峰时数一次，slow随之变成正值，对于负坡、平值道理是一致的； 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int fast=0;  //开始时快慢都为0
        int slow=0;  
        int result=1; //开始时那个点就算长度1
        for(int i=0;i+1<nums.size();i++){
            fast=nums[i+1]-nums[i]; 
            if((fast>0&&slow<=0)||(fast<0&&slow>=0)){  //快慢指针有梯度差异都会++
                result++;
                slow=fast;  //如果写在外面，那么平坡导致slow=0，升坡导致fast>0，会计算错误，因此只有fast遇到下降或者上升（变号）才会更新慢指针
            }
        }
        return result;
    }
};

3. 最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

exmaple: 输入: [-2,1,-3,4,-1,2,1,-5,4] 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

方法一：暴力超时版 j循环找出从i字符到末尾的最大子序和，i循环找出使得子序和最大的i，题目不要求输出数组，仅要求返回子序和结果。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int result = -10000;
        int temp = 0;
        for(int i = 0; i< nums.size();i++){
            for(int j = i; j<nums.size();j++){
                temp +=nums[j];
                result = temp > result ? temp:result;
            }
            temp = 0;
        }
        return result;
    }
};

方法二：贪心算法 放弃使用j循环寻找某个i的最大子序和，单次i循环内，如果加入某个数使得子序和小于0，就需要重新计算子序和，因为当前子序和加后面的数，必然小于后面的数相加，所以剩下的也没必要算了，继续循环i即可； 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int temp = 0; 
        int result = -10000;  //题目
        for(int i = 0 ;i<nums.size();i++){
            temp += nums[i];
            result = temp>result ? temp : result;
            if(temp <= 0)
                temp= 0;
        }
    return result;
    }
};

  • 空间复杂度：temp记录结果，O(1)

  • 时间复杂度：一个for循环，每个for循环计算temp，一次遍历可以得出答案，O(n)

4. 买卖股票的最佳时机II

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

example: 输入: [7,1,5,3,6,4] 输出: 7 解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

实际题目的意思就是：找出顺序数，计算所有顺序数之间的差然后求和；例如prices = [1,2,3,4,5]，结果就是4；

方法一：排除逆序法 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        long result = 0; //题目范围
        int i = 0;
        while(i<prices.size()-1){  //循环数组
            while(i<prices.size()-1&&prices[i]>=prices[i+1])  //跳过所有逆序
                i++;
            if(i<prices.size()-1&&prices[i]<prices[i+1])
                result += (prices[i+1]-prices[i]);  //顺序计数
            i++;
        }
        return result;
    }
};

  • 空间复杂度： 一个result，O(1)

  • 时间复杂度： 一次循环能找出答案，内循环只是跳过逆序，O(n);

方法二：简写法 排除逆序已经有贪心算法的思想了，参考答案更简洁而已，复杂度是相同的。 

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int result = 0 ;
        for(int i=0;i<prices.size()-1;i++){
            result += max(prices[i+1]-prices[i],0);
        }
        return result;
    }
};

5. 跳跃游戏

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

example1:输入：nums = [2,3,1,1,4] 输出：true 解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

example2:nums = [3,2,1,0,4] 输出：false 解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

错误的分析：确保最后一位前至少有一位数字满足数字+下标>=最后一位的下标，能通过大部分测试，但是少部分特例是很痛苦的，例如如何保证这一位是可达的、开始时就跳不了怎么办，可能不得不面向“测试用例”编程，放弃这种写法。

遍历数组，问题在于我们能确定是否至少某个数字起能到达终点，但是无法判断该数字能否到达；另一种极端是能判断每个数字是否到达，但是缺乏了跳跃到达这种情况；痛苦的事情在于如何同时表达既可以跳跃到终点，也可以逐步到终点，一个cover遍历可以实现这种写法，值得学习：每到达一个新数字，更新可达范围； 

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    bool canJump(vector<int>& nums) {
        int cover = 0;
        for(int i = 0 ;i<=cover;i++){  //判断cover能否覆盖终点
            cover = max(nums[i]+i,cover);  
            if(cover>=nums.size()-1)
                return true;
        }
        return false;
    }
};

6. 跳跃游戏 II

给定一个非负整数数组，你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:

输入: [2,3,1,1,4] 输出: 2 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

说明: 假设你总是可以到达数组的最后一个位置。

这里确保了最后一个位置是可达的，因此既可以遍历数组，也可以遍历cover，我们仍采用cover；cover_next的逻辑和上面是一致的，更新每次数字的可达范围，但是这个cover_next不仅仅是满足可达范围，而且是最大的可达范围，因为每次的i会遍历到cover_last，即当前数字对应的所有可达数字都会被遍历，并且找出这一组的最大可达坐标作为下次遍历的终点，这种情况代表每次的i循环都在走最大一步，因此得到步数结果是最少的，记录步数，终点大于数组末尾直接返回即可； 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int jump(vector<int>& nums) {
        int result = 0;
        int cover_last = 0;
        int cover_next = 0;
        if(nums.size()==1)  //测试为0，特意写成0
            return 0;
        for(int i = 0; i <=cover_last; i++){  
            cover_next = max(nums[i]+i,cover_next);  //找到当前数字的最大范围
            if(i==cover_last){   //i走到了上次的最大范围末尾，确保cover_next是最大范围
                result++;  //计数
                cover_last = cover_next; //下次最大范围
                if(cover_next>=nums.size()-1) //到终点跳出
                    break;
            }
        } 
        return result;
    }
};

  • 空间复杂度：常数级变量，O(1)

  • 时间复杂度：一次数组遍历可以得到答案，O(n)

7. K次取反后最大化的数组和

给定一个整数数组 A，我们只能用以下方法修改该数组：我们选择某个索引 i 并将 A[i] 替换为 -A[i]，然后总共重复这个过程 K 次。（我们可以多次选择同一个索引 i。）

以这种方式修改数组后，返回数组可能的最大和。

example:输入：A = [4,2,3], K = 1 输出：5 解释：选择索引 (1) ，然后 A 变为 [4,-2,3]。

问题分析:K存在两种情况，K是奇数或者偶数；数组存在三种情况叠加：数组存在元素全大于0、存在0、存在负数，最复杂的情况是数组存在负数的情况，因为它和本身负数个数和K的个数都相关，应该先优先处理；思路是消耗K，将最小的负数转换成整数，如果K处理完负数仍有余量，再去处理一个非负数列，有0直接返回结果，正序列挑最小的变负；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int largestSumAfterKNegations(vector<int>& nums, int k) {
        sort(nums.begin(),nums.end());  //从小到大排序
        int i = 0 ;
        while(i<nums.size()&&nums[i]<0){  //小于0元素消耗k变正
            nums[i]=-nums[i];
            k--;
            i++;
            if(k==0)  //未变完K就归0
                return accumulate(nums.begin(),nums.end(),0); //直接数组求和，sum初始值为0
        }
        if(k%2==0)  //k是偶数，正数不用变号
            return accumulate(nums.begin(),nums.end(),0); 
        sort(nums.begin(),nums.end()); //k是奇数，找出最小奇数
        return accumulate(nums.begin(),nums.end(),-2*nums[0]); //最小正数变负再求和 = 直接求和-2倍最小正数
    }
};

  • 空间复杂度：原地操作，但sort的快排应该用了1个暂存变量，仍然是常数级的，O(1)

  • 时间复杂度：sort首先排序，排序算法最佳时间复杂度为O(nlogn)，然后遍历是O(n)，再排序，总体而言还是取其数量级，O(nlogn)

8. 加油站

在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。

给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则 保证 它是 唯一 的。

这里的唯一的意思是不需要我们保证，出题者保证用例的路径都是唯一解；

方法一：暴力超时版

题目分析：如果cost数组之和大于gas之和，肯定返回-1；下一个任务是表达循环关系，因为我们的遍历量i不能无限递增，通过取余变成圆周路径；第三个是计算每一次开车的余量，计算剩余值，剩余值一旦为负数，放弃这个遍历结果； 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        if(accumulate(gas.begin(),gas.end(),0)<accumulate(cost.begin(),cost.end(),0))
            return -1;
        for(int i=0;i<gas.size();i++){
            int remain = gas[i] - cost[i]; //计算起点消耗
            int j = (i+1)%gas.size();  //计算下一个值坐标，有可能拐回第一个数
            while(remain>=0&&j!=i){  //可以起飞且未回到起点
                remain += gas[j]-cost[j]; //计算下一个
                j = (j+1)%gas.size();
            }
            if(j==i)   //成功遍历一周
                return i;
        }
        return -1;
    }
};

  • 空间复杂度：O(1)

  • 时间复杂度：每个起点都要尝试环绕一圈，O()

方法二：全局排除法 原博主提供另一种很好的思路，我也没有想到这种排除方法：主要看三方面，首先从0点开始计算剩余量，如果0符合，0就是唯一解（题目本身唯一）；如果0不符合（剩余油量出现负数，且记录最大负数），就计算从末尾计算到某个点i，产生的剩余油量能够“填平”这个负数，无论从哪个点先出发，整个过程对应的最大负数都是一定的，既然末尾到i能够抵消这个最大负数，那么从i走到末尾相当于加油（抵消负数是i到末尾路径共同结果），这个油量肯定也能够保证整个路径剩余油量不会出现负数，除非油量本身小于消耗量；同理，计算1作为起点，计算0到i剩余油量填平1起始路径最大负数也可以，只是这种方法的数学表示更加麻烦；

这种方法只需要两次遍历：一次计算最大负数，一次计算最大负数油量填平位置； 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int min = gas[0] - cost[0];
        int sum = 0;
        for(int i =0;i<gas.size();i++){
            sum += gas[i]-cost[i];
            min = sum<min?sum:min;
        }
        if(min >= 0)   //0本身能填平最大油量负数
            return 0;
        int sum1;
        for(int i = gas.size()-1;i>=0;i--){  //从末尾开始查找哪次累计加油可以填平
            sum1 = gas[i] - cost[i];
            min +=sum1;
            if(min>=0)
                return i;
        }
        return -1;  //根本填不平
    }
};

  • 空间复杂度：O(1)

  • 时间复杂度：最多遍历两次能得到答案，O(n)

这种方法利用另一个循环寻找i的位置，注意，找到最小负数，后面的一位未必就是可以作为起点的位置，例如最小负数后面补偿了2，然后再-1，这样从这一位开始就会断在-1了，方法三提供了另一种寻找能填平负数的i坐标方法，只需要循环一次数组即可得到答案；

方法三：局部优化法 temp_sum会记录使得累加为负的坐标i，然后清零再寻找后面是否仍存在负量（会使无法环路驾驶），确保后面的补偿量都是正的补偿量，排除了2后面还有-1这种断路；方法二和方法三都体现了贪心算法思想，但是算法比较大胆，如果没做过相关题目确实不敢写出； 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int sum =0;
        int temp_sum = 0;
        int result = -1;
        for(int i=0; i<gas.size(); i++){
            sum += gas[i] - cost[i];   //记录从0到末尾累加
            temp_sum += gas[i] - cost[i];  //寻找负量累加
            if(temp_sum<0){  //记录最后一次负量的坐标
                temp_sum = 0;  //清零再计算是否为负
                result = i+1;
            }
        }
        if(temp_sum==sum)  //说明没有出现负量，0就是答案
            return 0;
        if(sum<0)  //说明油量少于路径消耗量，不可能有答案
            return -1;
        return result; //返回起始坐标
    }
};

  • 空间复杂度：O(1)

  • 时间复杂度：最多遍历一次能得到答案，O(n)

9. 分发糖果

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。

你需要按照以下要求，帮助老师给这些孩子分发糖果：

  • 每个孩子至少分配到 1 个糖果。

  • 相邻的孩子中，评分高的孩子必须获得更多的糖果。

那么这样下来，老师至少需要准备多少颗糖果呢？

示例 1:

example1:输入: [1,0,2] 输出: 5 解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。

example2: 输入：ratings = [1,2,2] 输出：4 解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。 第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

先从左向右遍历，右边大的等于左边大的糖果数+1，然后从右向左遍历，左边大的糖果数也等于右边+1，第二次遍历取糖果数的最大值，防止从右边遍历后，赋值变得更小了，使右边评分高的糖果数目异常减小。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int candy(vector<int>& ratings) {
        vector<int>result(ratings.size(),1);
        for(int i=0; i<ratings.size()-1; i++){  //从左往右，右边分高增加糖果
            if(ratings[i]<ratings[i+1])
                result[i+1] = result[i]+1;
        }             
        for(int i = ratings.size()-1; i>=1; i--){ //从右往左，左边分高增加糖果，只能增加，不能反向降低，取max
            if(ratings[i]<ratings[i-1])
                result[i-1] = max(result[i-1],result[i]+1);
        }
        return accumulate(result.begin(),result.end(),0); //数组和，初始值为0
    }
};

动态规划篇

动态规划问题可以从两个思路出发，其一是递推公式，从初始状态如何推导下一个状态，涉及状态转移公式；其二是递归子问题的方式，这是后面增加的思路，动态规划通常需要达到目的n，就可以递归n-1问题或者n-i问题，加入记忆化搜索剪枝；将递归换循环数组推导，就是动态规划方法，两种思路是殊途同归的。

1. 斐波那契数列

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1 F(n) = F(n - 1) + F(n - 2)，其中 n > 1 给定 n ，请计算 F(n) 。

example: 输入：n = 2 输出：1 解释：F(2) = F(1) + F(0) = 1 + 0 = 1

递归法

知道前后项关系可以用递归法，让程序算去吧。 

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int fib(int n) {
        if(n==0)
            return 0;
        else if(n==1)
            return 1;
        else
            return (fib(n-1)+fib(n-2));
    }
};

  • 空间复杂度：每个调用层记录一个和结果，n有n个调用栈，O(n)

  • 时间复杂度：回溯需要回溯到n==1或者n==0的情况，函数每次都会产生2次调用，O()

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int fib(int n) {
        if(n<=1)
            return n;
        vector<int>dp(n+1);
        dp[0] = 0;
        dp[1] = 1;
        for(int i =2;i<=n;i++){
            dp[i] = dp[i-1]+dp[i-2]; 
        }
        return dp[n];
    }
};

  • 空间复杂度：只返回了n，但实际上整个数组都可以被引用，这个可以优化成O(1)，目前是O(n);

  • 时间复杂度：n次循环计算，O(n)

2. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

example：输入： 3 输出： 3 解释： 有三种方法可以爬到楼顶。 1 阶 + 1 阶 + 1 阶 1 阶 + 2 阶 2 阶 + 1 阶

枚举1-6级：

阶数 1 2 3 4 5 6
方法数 1 2 3 5 6 13

所以这是斐波那契数列的应用，代码同上题，初始条件需要对齐到3，因为i==2不具备计算条件： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int climbStairs(int n) {
        if(n==1)
            return 1;
        vector<int>dp(n+1);
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 2;  //manual
        for(int i =3;i<=n;i++){
            dp[i] = dp[i-1]+dp[i-2]; 
        }
        return dp[n];
    }
};

3. 使用最小花费爬楼梯

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

example:输入：cost = [1,100,1,1,1,100,1,1,100,1] 输出：6 解释：你将从下标为 0 的台阶开始。 - 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。 - 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。 - 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。 - 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。 - 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。 - 支付 1 ，向上爬一个台阶，到达楼梯顶部。 总花费为 6 。

记忆化搜索:通过率283/284

第n级阶梯，可以是n-2级爬2级，也可以是n-1级爬1级，这就是子问题。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public: 
    unordered_map<int,int>umap;
    int dfs(vector<int>& cost,int i){
        if(i<=1)
            return 0;
        if(umap[i]!=0)
            return umap[i];
        return umap[i]=min(cost[i-1]+dfs(cost,i-1),cost[i-2]+dfs(cost,i-2));
    }

    int minCostClimbingStairs(vector<int>& cost) {
        int result = 0;
        result += dfs(cost,cost.size());
        return result;
    }
};

动态规划

dp[i]代表第一步到i-1步或者i-2步累计支付的金钱，起始时dp[0]和dp[1]都代表0步，不需要计算花费，dp[2]开始将比较走一步还是走两步的最低成本，枚举开始几种情况：

  • dp[0]=0，因为开始就是0

  • dp[1]=0，从0选择往上爬=cost[0]，直接选择1为0，较小为0；

  • dp[2] = min(cost[0],cost[1])；既可以从0网上爬两格，即cost[0]；也可以从1往上爬1格，即cost[1]，取较小的。

子问题就以上三种，

dp[3] = min(dp[2]+cost[2],dp[1]+cost[1])，爬三格要么先爬两格，花费dp[2]，再网上一格即cost[2]，要么爬一格再向上爬，递推公式就出来了：

  • dp[i] = min(dp[i-2]+cost[i-2],dp[i-1]+cost[i-1])，dp[2]也满足这个，并不并入均可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n = cost.size();
        if(n<2)  //dp[0]/dp[1]=0;
            return 0;
        vector<int>dp(n+1);
        dp[2] = min(cost[0],cost[1]);
        for(int i=3; i<=n; i++){
            dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[n];
    }
};

4.不同路径

一个机器人位于一个 m x n 网格的左上角。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角。

问总共有多少条不同的路径？

方法一：纯数学问题：无论如何一共需要步，其中步需要向下走，无重复为组合数 ，计算这个数即可；

另外两种方案更加通用：

方法二：递归深度搜索（暴力超时版） 递归通过38/63，时间复杂度高。 

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int dfs(int i,int j,int m,int n){
        if(i>m||j>n)   //越界
            return 0;
        if(i==m&&j==n) //
            return 1;
        return dfs(i+1,j,m,n)+dfs(i,j+1,m,n);
    }
    int uniquePaths(int m, int n) {
        return dfs(1,1,m,n);   
    }
};
每次搜索都会产生两次调用，调用层次如下，数字代表位置坐标： DFS调用 因此树高=m+n-1；

  • 时间复杂度：O(2^{m+n-1})

  • 空间复杂度：考虑数量级，O(m+n)

方法三：动态规划

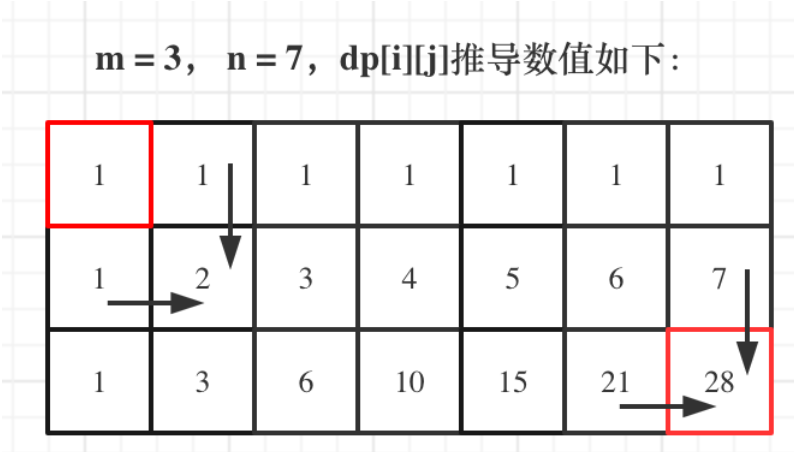
关键是得到推导数组，无论(m,n)是什么，其可以拆分成(m-1,n)和(m,n-1)，因为机器人只能向右或者向下移动，到达(m,n)前必须经过(m-1,n)和(m,n-1)，另外一个特性是开始时只向右或者只向下的路径只有一个方法，因为不能向上或者向左折返，就有了： 动态规划数组

于是就可以完成动态规划代码： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>>dp(m+1,vector<int>(n+1)); //m行n列,第0行、第0列无效
        for(int i=1; i<=m; i++){  //从1开始计数
            for(int j=1; j<=n; j++){ //1开始计算
                dp[i][1] = 1;  //第一列为1
                dp[1][j] = 1;  //第一行为1
                if(i>=2&&j>=2)  //其余为左边和上边方法递推
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m][n];

    }
};

  • 空间复杂度：二维数组，O(mn);

  • 时间复杂度：二维数组循环，O(mn);

5. 不同路径II

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

example:输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]] 输出：2 解释：3x3 网格的正中间有一个障碍物。 从左上角到右下角一共有 2 条不同的路径： 1. 向右 -> 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 -> 向右

问题分析：和上题的唯一不同就是存在障碍物，所以某些路径会被排除，处理思路是完全一样的，只是条件稍微变化。

方法一：递归深度搜索（暴力超时版） 和原来的思路是一致的，只需要增加判断是否障碍物条件即可，很方便，但是时间复杂度很高。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int dfs(int i,int j,vector<vector<int>>& obstacleGrid){
        int m = obstacleGrid.size();
        int n =obstacleGrid[0].size();
        if((i>m)||(j>n)||obstacleGrid[i-1][j-1]==1)
            return 0;
        if(i==m&&j==n)
            return 1;
        return dfs(i+1,j,obstacleGrid)+dfs(i,j+1,obstacleGrid);
    }


    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        return dfs(1,1,obstacleGrid);
    }
};

  • 时空复杂度：同前一题

方法二：动态规划 思路和原来也是一样的，填充逻辑稍微增加了一点：先填充两边，如果有障碍后续全记为0；然后填充内部，有障碍将该点dp记为0代表该路径不可通； 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        if(obstacleGrid[0][0]==1)  //一开始有障碍肯定不可达
            return 0;
        int m = obstacleGrid.size();  //行数
        int n = obstacleGrid[0].size(); //列数
        int dp[m][n];
        dp[0][0] = 1;  //确保一开始无障碍
        for(int i = 1; i<m; i++){
            if(obstacleGrid[i][0]==1||dp[i-1][0]==0) //第一列有障碍记为0，或者前面已经遇到障碍被记0了
                dp[i][0] = 0;
            else
                dp[i][0] = 1;
        }
        for(int j = 1; j<n; j++){
            if(obstacleGrid[0][j]==1||dp[0][j-1]==0) //第一行有障碍，或者前面已经遇到过障碍
                dp[0][j] = 0;
            else
                dp[0][j] = 1;
        }
        for(int i = 1;i<m;i++){  //填充内部
            for(int j = 1; j<n; j++){
                if(obstacleGrid[i][j]==1)  //障碍位置0
                    dp[i][j]=0;
                else    
                    dp[i][j] = dp[i-1][j]+dp[i][j-1];  //其余同样计算
            }
        }
        return dp[m-1][n-1];
    }
};

  • 时空复杂度：同前一题

6. 整数拆分

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

example:输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

  • 说明: 你可以假设 n 不小于 2 且不大于 58。

错误的分析：首先想到的是正方形面积原理，假设只分成两个正整数，肯定是对半分的乘积最大，因此一个数要不断地拆分，这是一种二叉树结构，例如52分成两个26，4个13......，停止拆分应该是遇到3或者4，因为2拆分成1×1，是变小了，3拆分成1×2也是变小了，4拆与不拆答案是一样的，5拆成2×3=6变大了，因此5（包含）以上都应该拆；

反例：这个二分法思路对两个正整数以上的不太适用，对一些数字（8、9、14、15、20等），先不等分比等分得到的乘积更大，也即不一定是等分成2份最大，而是等分成近似的m份，才是最大，例如8分成2、3、3比4、4乘积更大。

暴力递归

这道题手写不出递推公式，只能使用暴力循环和递推了，对于每个正整数n，i从1开始遍历，乘积最大的结果要么是(这个数-i)*i，要么就是继续拆分(这个数-i)再乘i；

这里完全可以遍历到i<= n/2，因为要分成n的m等分，n/2已经包含范围了，这个优化提前剪枝了一部分循环，通过率从通过30/50升到31/50。。。再优化就是动态规划的写法了。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int travel(int n){
        int result = 0;
        if(n<=3)   //3前面模拟出来都是n-1，n=1是无效数据（因为1*0=0），判断小于等于2也可
            return n-1;
        for(int i=1; i<=n-1; i++){  //可以为i<=n/2
            result = max(result,max((n-i)*i,travel(n-i)*i));
        }
        return result;
    }


    int integerBreak(int n) {
        int result = travel(n);
        return result;
    }
};

动态规划

动态规划不用递归栈记录结果，而是使用dp数组记录结果，递推回去就能找到某个数的最大乘积，写完递归容易理解： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int integerBreak(int n) {
        if(n==2)  //2只能拆成1×1
            return 1; 
        vector<int>dp(n+1);  //vector和int[][]区别是前者会初始化为0，这里需要比较dp，需要初始化，使用vector
        //dp[1] = 0;  //1是无效数据
        dp[2] = 1;
        for(int i =3; i<=n; i++){
            for(int j = 1;j<=i-1; j++)  //j<=i/2更优，因为i要等分乘m份，j作为一份的值必然小于i的一半
                dp[i] = max(dp[i],max(j*dp[i-j],j*(i-j)));
        }
        return dp[n];
    }
};

  • 空间复杂度：每个n都是可知的，O(n)

  • 时间复杂度：内外循环，都是与n相关的二次方数量级，因此O()

7. 不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

二叉搜索树定义是： 每个结点必须满足：左结点<根结点<右结点，其左子树的元素也小于根结点，右子树元素大于根结点；

错误的题目分析：首先确定根结点，这个根结点决定了左右子树的元素；左右子树有几个结点，其分布情况就是全排列种可能，例如左子树有5个结点，右子树3个结点，就是种可能，然后计算不同根结点的划分子树情况即可。

全排列种可能是不对的，例如n==4，根结点是1时，右子树是2，3，4时，只有5种可能，而不是全排列的6种可能，因为排列1、3、2、4（3接1时），只有一种可能，而不是两种，2，4只能分别在3结点的左右，所以全排列会算多了；不能用阶乘的方法，但根结点分割的方法没有问题，只需要使用dp记录某个点的可能数即可，自然写出：

  • 结点数为2，根结点+左子树/根结点+右子树，2种；

  • 结点数为3，1、2、3结点轮流根结点，剩下两个结点为子树，全放在左边就是2种（3为根），全放在右边也是两种（1为根），一边一个1种（2为根），因此是5种

  • 结点数为4，1、2、3、4轮流根结点，三个放左边（4为根，说了不是全排列，而是前面递推的5种），然后三个放右边（1为根），2+1、1+2组合等。

递推就出来：结点数为n，1——n轮流根结点，左右子树分割成0+n-1、n-1+0、1+n-2、n-2+1...等组合

动态规划： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int numTrees(int n) {
        if(n<=1)  
            return 1;
        if(n==2) 
            return 2;
        vector<int>dp(n+1);
        dp[0] = 1;  //为了计算，左子树为结点数为0，右子数结点数为n，这种情况取决于右子树，左子树置1
        dp[1] = 1; //1个结点为1种可能
        dp[2] = 2; //2个结点为2种可能
        int i,j;        
        for(int i = 3; i<=n; i++){  //从3计算到n（实际上n/2以后和之前的是对称的，可以分开，但是要讨论奇偶）
            for(int j = 0;  j<=i-1 ; j++)  //左子树放0个，右子树放i-1个/左放1，右放i-2.....
                dp[i] += dp[j]*dp[i-j-1]; // 相乘、叠加
        }
        return dp[n];
    }
};

8.背包问题

小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。他需要带一些研究材料，但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等，它们各自占据不同的空间，并且具有不同的价值。

小明的行李空间为 N，问小明应该如何抉择，才能携带最大价值的研究材料，每种研究材料只能选择一次，并且只有选与不选两种选择，不能进行切割。

第一行包含两个正整数，第一个整数 M 代表研究材料的种类，第二个正整数 N，代表小明的行李空间。

第二行包含 M 个正整数，代表每种研究材料的所占空间。

第三行包含 M 个正整数，代表每种研究材料的价值。

example:
输入：
6 1
2 2 3 1 5 2
2 3 1 5 4 3 输出：5

递归解法

递归回溯法可以遍历各种组合，并且计算空间space不超出N情况下value的最大值，这是一种暴力解法（由于时间超限无法保证完全正确，但测试用例和自定义一些用例是没问题的）： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <vector>
#include <numeric>  //accumulate
using namespace std;

class Solution{
public: 
    int result=0;
    int N;
    int M;
    vector<int>temp_value;  //存储每次存放的价值
    vector<int>temp_space;  //存储每次存放的空间占用
    void travel(vector<int>space,vector<int>value,int start){
        int sum_space = accumulate(temp_space.begin(),temp_space.end(),0); //目前价值和
        int sum = accumulate(temp_value.begin(),temp_value.end(),0);  //目前占用空间和
        if(sum_space<=N){   //空间不超出，记录result
            result = sum>result?sum:result;  //新结果大才记录，注意记录完不能return
        }
        if(start>=M||sum_space>N)  //空间超过或者数组越界才return
            return;
        for(int i=start; i<M;i++){
            temp_value.push_back(value[i]);  //入栈
            temp_space.push_back(space[i]); 
            travel(space,value,i+1);
            temp_value.pop_back();
            temp_space.pop_back();
        }
    }
    int get_result(vector<int>space,vector<int>value){
        travel(space,value,0);
        return result;
    }
};

int main(){
    int M,N;
    cin>>M>>N;  //输入种类M，空间大小N
    
    vector<int>space(M) ;
    vector<int>value(M);
    
    for(int i=0;i<M;i++){ //输入每个物品空间占用大小
        cin>>space[i];
    }
    for(int i=0;i<M;i++){ //输入每个种类物品的价值
        cin>>value[i];
    }
    Solution mySolution;
    mySolution.M = M;
    mySolution.N = N;
    int result = mySolution.get_result(space,value);
    cout<<result<<endl; //结果
    return 0;
}

  • 时间复杂度：每种物品都有选和不选两种可能，都会被递归遍历到，O(2^{M});

  • 空间复杂度：每个物品被选入，最大是O(M)；

01背包理论——动态规划解法

递归法对于解决这类问题耗时是很长的，动态规划应对这种问题也能够解决，而且复杂度更优化，这就是动态规划的背包理论。假设现在三个物品的价值和重量分布为：

物品1 物品2 物品3
重量 1 3 4
价值 15 20 30

为了衡量这个物品与重量的选择分布，给出一个dp数组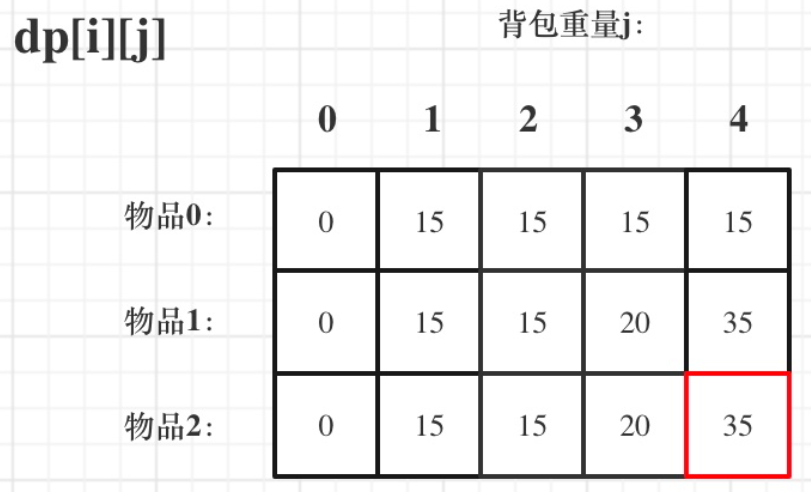： dp数组

dp值的含义是：某个背包质量下，能够放下的第一个物品到第i个物品的最佳搭配，例如(i=2,j=3)，代表背包重量为3，这个前提下任意存放物品0、1、2得到的最大价值。如果i==1，就只能任意存放物品0、1；

二维数组的每一列，代表背包重量一定的情况下，能放下的不同价值，其中的最大值就是上面背包问题的答案；

如何从一列的前一个元素推导下一个元素是逻辑的关键，简单情况是例如重量等于2时，这种情况遍历物品，只有物品0重量小于2，所以这一列全是15，下一个元素就等于上一个元素；而如果背包重量为3，此时如何从物体0的15推导出物体1的20呢？这就需要比较存放物品0的总价值（15）以及存放物品1（value[i]）后再存放其他物品的价值（j-wight[i]），取它们之间的最大值即可。

初始化时第一列重量为0，恒定为0；第一行为物品0，不存在置换情况，全是物品0价值（确保j需要大于物品0重量）。

下面代码就是需要构建这样的二维数组，根据背包重量、物体类别取到坐标i、j的dp值，解决背包问题：

动态规划法： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <iostream>
#include <vector>
using namespace std;

class Solution{
public:
    int M,N;
    Solution(int M,int N):M(M),N(N){};
    int get_result(vector<int>space, vector<int>value){
        vector<vector<int>>dp(M,vector<int>(N+1));
        for(int j = 1; j <= N; j++){  //第一行，背包大于物品0，放入物品0
            if(space[0] <= j)
                dp[0][j] = value[0];
        }      
        for(int i = 1; i < M; i++){ 
            for(int j =1;j <= N; j++){
                if(j < space[i])  //当前物品空间大于背包空间，不用考虑放入
                    dp[i][j] = dp[i-1][j];
                else  //可以放入考虑是否放入
                    dp[i][j] = max(dp[i-1][j],dp[i-1][j-space[i]]+value[i]); 
            }    
        }
        return dp[M-1][N];  //返回结果，M-1对于第M个物品，N对于重量N
    }
};


int main(){
    int M,N;
    cin>>M>>N;
    
    vector<int>space(M);
    vector<int>value(M);
    
    for(int i=0;i<M;i++){
        cin>>space[i];
    }
    for(int i=0;i<M;i++){
        cin>>value[i];
    }
    
    Solution mySolution(M,N);
    int result = mySolution.get_result(space,value);
    cout << result <<endl;
    return 0 ;
}

  • 空间复杂度：二维数组，

  • 时间复杂度： 二维数组，

9. 分割等和子集

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

example:输入：nums = [1,5,11,5] 输出：true 解释：数组可以分割成 [1, 5, 5] 和 [11] 。

暴力超时版：递归回溯法，可以遍历每一种组合，查看其两倍是否等于原来数组的和，原题目没有要求给出组合，使用flag记录即可，因此递归这种方法也比较浪费。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<int>temp;
    int flag = 0;
    void travel(vector<int>& nums,int target,int start){
        int div_sum = accumulate(temp.begin(),temp.end(),0);
        if(div_sum*2 == target){  //符合条件
            flag = 1;  //不要求组合，记录标记位即可
            return;
        }
        if(div_sum*2>target)
            return;
        for(int i = start; i<nums.size();i++){
            temp.push_back(nums[i]);
            travel(nums,target,i+1);
            temp.pop_back();
        }
    }

    bool canPartition(vector<int>& nums) {
        int target = accumulate(nums.begin(),nums.end(),0);
        travel(nums,target,0);
        if(flag==1)
            return true;
        return false;
    }
};

  • 空间复杂度：数组长度为n，temp数组可以存储n个数，以及flag记录状态，O(n)；

  • 时间复杂度：为；

动态规划：这里仍然可以看成是一种背包问题。m表示行数，每一行表示能够自由组合的数组元素数目，例如第三行只能使用数组前三个元素进行组合（这个可以优化成一维，因为数组元素是任意使用的）；n代表列数，每一列列编号为j，同一列元素代表不大于j的最大元素组合。这就是dp[i][j]的含义。

如果想要知道一个数组能否分割出和为其一半的子集，只需要知道不大于这个和的情况下，数组元素自由组合的最大值能否到达这个和，所以代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int m = nums.size();  //行数
        int n = accumulate(nums.begin(),nums.end(),0); //数组和
        if(n%2==1)
            return false;  //为单数不可能分割成两个子集
        n /= 2;  //列数
        vector<vector<int>> dp(m,vector<int>(n+1)); //0固定占额外一列
        for(int j = 1; j<=n; j++){
            if(nums[0]<=j)   //j看成是目标和，小于目标和的元素组合都可以加入dp计算
                dp[0][j] = nums[0]; 
        }    
        
        for(int i=1; i<m; i++){
            for(int j=1; j<=n; j++){
                if(nums[i]>j)   //某个元素值本身大于目标和
                    dp[i][j] = dp[i-1][j]; //不加入这个元素
                else //元素值小于要求和
                    dp[i][j] = max(dp[i-1][j],dp[i-1][j-nums[i]]+nums[i]); //求最大组合和
            }
        }
        return dp[m-1][n]==n;  //组合和恰好是目标和，说明目标和可达
    }
};

数组长度为m，数组和的一半（目标和）为n：

  • 时间/空间复杂度：O(mn)

10. 最后一块石头的重量II

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

  • 如果 x == y，那么两块石头都会被完全粉碎；

  • 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。 最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

example:输入：stones = [2,7,4,1,8,1] 输出：1 解释： 组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]， 组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]， 组合 2 和 1，得到 1，所以数组转化为 [1,1,1]， 组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

题目分析：表面上涉及了石头的碰撞和转化，好像很复杂，事实上一个数组给定，返回的最小重量就已经确定，其值就是将石头分成两半，这两半的最小差异，所以还是一种背包问题。

对其中一半应用dp数组，得到的dp结果就是这个数组所有石头自由组合出的、不超过重量一半、但最接近一半的重量组合，因此另一半与它的差就是最小重量。

以下代码，和上题逻辑是基本一致的。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        int sum = accumulate(stones.begin(),stones.end(),0);
        int m = stones.size();  //行数
        int n = sum/2;  //列数，列数代表最大重量
        vector<vector<int>>dp(m,vector<int>(n+1));

        for(int j = 1; j<=n;j++){  //j代表最大重量，j列元素代表不超过j的最大组合重量
            if(stones[0]<=j)
                dp[0][j] = stones[0];
        }
        
        for(int i=1; i<m; i++){
            for(int j=1; j<=n; j++){
                if(stones[i]>j)
                    dp[i][j] = dp[i-1][j];
                else
                    dp[i][j] = max(dp[i-1][j], dp[i-1][j-stones[i]]+stones[i]);
            }
        }
        return sum - dp[m-1][n] - dp[m-1][n]; //sum - dp[m-1][n]是另一半对应的重量，再减一次表示两个子集的最小差
    }
};
数组长度为m，石头数组重量和的一半为n(向下取整)；

  • 时间/空间复杂度：O(mn)

11. 目标和（动态规划解决回溯组合问题）

给你一个非负整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。 返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

example：输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3

问题分析：首先在回溯或者动态规划中判断什么时候取“+”，什么时候取“-”都是困难的事情，例如通过DFS解决；这个问题也可以进一步转化一下，事实上这个问题等效于“在nums中找出目标和为(target+sum(nums)/2)”的所有组合，简单证明如下: 

1
2
3
4
5
6
7
8
假设nums中负集和为left，正集和为right，它们组成的目标和可以构成target，即
-left + right = target；

而sum = left + right = nums.sum();

故正集right = (target + sum)/2 ；

且right只能为偶数，因为整数的组合加减不可能出现小数。

因此只需要求目标和为right的正集，剩下的数记为负集，即得到答案；

暴力幸存版：回溯算法

回溯算法的方法：搞明白这是一种不回头选择写法，递归去选择重复元素，根据例子尽管后面产生的数字组合是一致，也无需进行去重，虽然暴力，但本题难能可贵地没有超时，效率依然很低。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//问题等效于求新目标和right=(目标和+sum）/2，right可达，目标和一定可达
class Solution {
public:
    vector<int>temp; 
    int result =0;
    void travel(vector<int>& nums, int right, int start){
        int sum = accumulate(temp.begin(),temp.end(),0);
        if(sum==right){ //不能return，当前满足right，插入其他数（例如0）仍然能满足right
            result++;
        }
        if(sum > right)
            return;
        for(int i=start; i<nums.size(); i++){
            temp.push_back(nums[i]);
            travel(nums,right,i+1);
            temp.pop_back();
        }
    }

    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = accumulate(nums.begin(),nums.end(),0);  
        if(target > sum)  //非必须剪枝
            return 0;
        if((sum+target)%2==1)   //必须：否则会导致新目标和不准确
            return 0;
        travel(nums,(sum+target)/2,0);  //(sum+target)/2是新目标和，必须保证(sum+target)是偶数
        return result;
    }
};

  • 空间复杂度：temp存储了结果，O(n);

  • 时间复杂度：每个元素都要考虑选不选，

二维动态规划法（初始化复杂的01背包问题）

既然涉及选和不选，就说明这也是一种背包问题。其实问题转化成组合和后，就很容易想到，构造二维dp数组，题目类型和9. 分割等和子集貌似差不多，以那题的思路，例如[1,1,1,1,1]，相同的方法构造的dp数组是：

0 0 1 1 1 1
0 1 1 2 2 2
0 1 2 2 3 3
0 1 2 3 3 4
0 1 2 3 4 4

那道题只是判断一个正整数数组能否分割成两个和相等的子集（即找到目标和为target=sum/2的子集），这是一种bool问题，正整数限定的最大组合数一定是右下角，且取决于target列前面的元素；如果是非正整数，则应该遍历target以外的所有列、所有行；

对于本题，需要找的是不同的组合情况，现在target是3，说明目标和是(sum+target/2) = 4，然而这里只有3种最大组合数为4的情况，说明dp的构造思路需要改变，如下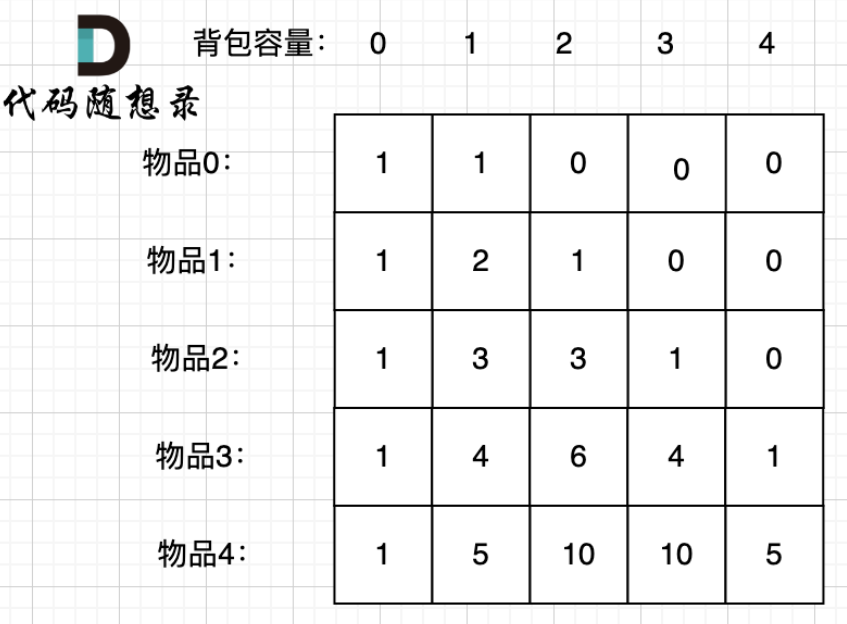： dp数组 i、j仍然分别限定组合对象、背包容量，但是j不再代表最大的背包容量，而仅仅是背包容量；此时dp[i][j]的意义是能满足容量j情况下（恰好为j，不能大也不能小）自由组合对象0——i的组合和为j的数量，也即如果某个j列的dp等于0，说明任何i的组合都无法刚好达到这个容量。

对应的初始化、递推思路都发生了改变，鉴于图片例子并不能很好覆盖其他例子，这里使用其他的例子，例如输入数组[3,2,0,4,0]，target定义为1，即目标和对应为5，构造的dp行数为5（size），列数为目标和+1（注意这里是新的目标和，即right值），即6；dp具体如下 

1
2
3
4
5
6
数组\下标     0       1       2       3       4       5      
    3        1       0       0       1       0       0      
    2        1       0       1       1       0       1  
    0        2       0       2       2       0       2  
    4        2       0       2       2       2       2  
    0        4       0       4       4       4       4

初始化时，dp[0][0]恒定为1，因为背包为0容量情况下，不放物品0肯定都能满足0容量需求，为一种方法；第一列后面的数主要取决于是否有0，如果产生0，就需要累计（因为正负0都算不同的方法，纯目标和问题则无需这一步），第一行，如果物品0恰好为某和容量j，对应的dp[0][j]也是一种方法，记1；

初始化完成了第一列、第一行的初始化；

其他元素的递推还是从列开始看，每一列的下一个元素都是上一行的元素推导出来的，见代码： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
//问题等效于求新目标和new_target=(目标和+sum）/2，new_target可达，目标和一定可达
class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int m = nums.size();
        int n = accumulate(nums.begin(),nums.end(),0);
        if(abs(target) > n)   //例子有target为负的情况
            return 0;
        if((target+n)%2==1)  //target+n不能是奇数
            return 0;
        int new_target = (target + n)/2; //right值
        vector<vector<int>>dp(m,vector<int>(new_target+1));  //因为是非负

        dp[0][0] = 1;//不放物品0恒满足容量0

        if(nums[0] <= new_target)  //重量范围在new_target以内，即j取得到nums[0]
            dp[0][nums[0]] = 1; //容量刚好为num[0]的算一种方法

        int zero_num = 0;
        for(int i=0; i<m; i++){  //第一列初始化
            if(nums[i]==0)
                zero_num++;  //有0情况翻倍，例如一个0对应2，两个0对应4，3个0对应8
            dp[i][0] = (int)pow(2.0,zero_num); //有0为2的zero_num次方，无0为1
        }
        
        for(int i=1; i<m; i++){  //递推
            for(int j =1; j<=new_target; j++){
                if(nums[i]>j)  //放入物品i超出背包重量
                    dp[i][j] = dp[i-1][j];  //继承
                else  //可以放入
                    dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]];  //原来的方法数 + 预留空间的方法数
            }
        }
        return dp[m-1][new_target];
    }
};

一维动态规划法

省去了二维复杂的初始化步骤，比较简单。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//问题等效于求新目标和new_target=(目标和+sum）/2，new_target可达，目标和一定可达
class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int m = nums.size();
        int n = accumulate(nums.begin(),nums.end(),0);
        if(abs(target) > n)   //例子有target为负的情况
            return 0;
        if((target+n)%2==1)  //target+n不能是奇数
            return 0;
        int new_target = (target + n)/2; //right值
        vector<int>dp(new_target+1);  //因为是非负

        dp[0] = 1;//不放物品0恒满足容量0

        for(int i=0; i<m; i++){  //注意，0要包含递推，从二维化知道其第一列的投影是冲突的。
            for(int j =new_target; j>=0; j--){
                if(nums[i]>j)  //放入物品i超出背包重量
                    dp[j] = dp[j];  //继承
                else  //可以放入
                    dp[j] += dp[j-nums[i]];  //原来的方法数 + 预留空间的方法数
            }
        }
        return dp[new_target];
    }
};

12. 一和零（多维度01背包问题）

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

example:输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。 其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

题目分析：从数组strs中挑选元素组成子集，只要子集长度最大（指子集字符串元素数量最多），且满足0和1的数量小于等于指定值即可。本质上是一种递归组合问题，自然可以使用路径规划解决，而且属于01背包问题，这题不一样的地方在于限制条件是0和1的数量，因此dp数组应该是三维的。（在前几个算法问题中dp数组只需要满足重量、或者大小条件即可，这里需要同时满足0和1的数量限制。

dp[i][j][k]的含义是：i个元素自由组合，0的数目不超过j，1的数目不超过k，三个前提下计算得到的最大长度。

除了增加维度，有一个细节应该注意：不应该无脑忽略j==0和k==0,即第二维和第三维的第一列的初始化，例如j==0，说明要求最多出现0个0，但是如果此时k!=0，即完全可以选择1、111等，说明j==0或者k==0应该是要假如初始化的；而不像过去的二维问题，背包容量为0，就不会放东西。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int l = strs.size();  //第一维，m第二维，n第三维；
        vector<vector<vector<int>>>dp(l,vector<vector<int>>(m+1,vector<int>(n+1)));

        //两个数组记录每个str的0和1数量；
        vector<int>zero_num(l);
        vector<int>one_num(l);
        for(int i=0; i<l; i++){
            for(int j=0; j<strs[i].size(); j++){
                if(strs[i][j]=='0')
                    zero_num[i]++;
                else
                    one_num[i]++;
            }
        }

        //只放strs[0],初始化:j、k作为容量，大于0和1数量才能放；本身strs[0]小于规定量才能放
        for(int j=0; j<=m; j++){  //初始化包含0！
            for(int k=0; k<=n; k++){
                if(j>=zero_num[0]&&k>=one_num[0]&&zero_num[0]<=m&&one_num[0]<=n)  //放得下
                    dp[0][j][k] = 1;   //放strs[0]
            }
        }

        for(int i=1; i<l; i++){
            for(int j=0; j<=m; j++){  //计算也可以包含0
                for(int k=0; k<=n; k++){
                    if(zero_num[i]>j||one_num[i]>k||zero_num[i]>m||one_num[i]>n) //放不下
                        dp[i][j][k] = dp[i-1][j][k];
                    else    //如果放得下，方法数记得+1.
                        dp[i][j][k] = max(dp[i-1][j][k],dp[i-1][j-zero_num[i]][k-one_num[i]]+1);
                }
            }
        }
        return dp[l-1][m][n];
    }
};

问题可进一步降为二维写法，略。

13. 完全背包问题

小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。他需要带一些研究材料，但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等，它们各自占据不同的重量，并且具有不同的价值。

小明的行李箱所能承担的总重量为 N，问小明应该如何抉择，才能携带最大价值的研究材料，每种研究材料可以选择无数次，并且可以重复选择。

输入描述 第一行包含两个整数，N，V，分别表示研究材料的种类和行李空间

接下来包含 N 行，每行两个整数 wi 和 vi，代表第 i 种研究材料的重量和价值

输出描述 输出一个整数，表示最大价值。

输入示例
4 5
1 2
2 4
3 4
4 5
输出示例
10

完全背包和01背包唯一区别：选择的物品可以重复无限次。

仍然按二维数组的方法给出：和01背包相比dp[i-1][j-space[i]]+value[i]，只有初始化和max比较两个地方出现差异，见注释，为什么是dp[i][j-space[i]]+value[i]而不是原来的dp[i-1][j-space[i]]+value[i]：原来要放入物体i，因为01背包的物体i是唯一的，因此一定不能从放过i物体的dp数组选择最大值，而现在物体i的数量是无限的，因此允许从dp[i]的数组选择最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <vector>
using namespace std;

class Solution{
public:
    int M,N;
    Solution(int M,int N):M(M),N(N){};
    int get_result(vector<int>space, vector<int>value){
        vector<vector<int>>dp(M,vector<int>(N+1));
        for(int j = 1; j <= N; j++){  
            if(space[0] <= j)
                dp[0][j] = dp[0][j-space[0]]+value[0];  //初始化时不要只写dp[0][j]=value[0]，因为现在一个物品也可以重复放入
        }      
        for(int i = 1; i < M; i++){ 
            for(int j =1;j <= N; j++){
                if(j < space[i])    //放不进去，仍然沿袭上一个
                    dp[i][j] = dp[i-1][j];
                else   //放的进去，第二个是dp[i]而不是dp[i-1]
                    dp[i][j] = max(dp[i-1][j],dp[i][j-space[i]]+value[i]); 
            }    
        }
        return dp[M-1][N]; 
    }
};


int main(){
    int M,N;
    cin>>M>>N;
    
    vector<int>space(M);
    vector<int>value(M);
    
    for(int i=0;i<M;i++){
        cin>>space[i];
        cin>>value[i];
    }

    
    Solution mySolution(M,N);
    int result = mySolution.get_result(space,value);
    cout << result <<endl;
    return 0 ;
}

14. 零钱兑换 II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

example:输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1 5=1+1+1+1+1

比一维方程复杂一点，但是比较能看出状态转移方程，核心是dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]，其中dp[i-1][j]是不使用硬币i的情况下组合成j的情况，dp[i][j-coins[i]]是使用了硬币i凑成j-coins[i]的方法数（这样再使用一次i就能凑成j了），所有元素的计算都起始来自边缘信息，然后开始计算，本质上还是一种递归/迭代思想，很巧妙。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int change(int amount, vector<int>& coins) {
        int m = coins.size();
        int n = amount;
        vector<vector<uint64_t>>dp(m,vector<uint64_t>(n+1));
        
        //初始化第一列，不放硬币为1，而不是0
        for(int i=0; i<m; i++){
            dp[i][0] = 1;
        }

        //初始化第一行，只放硬币0看是否能凑出
        for(int j=1; j<=n; j++){
            if(coins[0]<=j&&j%coins[0]==0) //coins[0]小于容量j,且coin[0]一个可以凑出j
                dp[0][j] = 1;
        }
        
        //递推
        for(int i=1; i<m; i++){
            for(int j=1; j<=n; j++){
                if(coins[i]>j)
                    dp[i][j] = dp[i-1][j]; //放不下，方法数不变
                else
                    dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]; //放得下加上
            }
        }

        return dp[m-1][n];
    }
};

15. 组合总和Ⅳ

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

example:输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。

这道组合总和有几个特性：每个元素可以无限选择，所以递归可以递归i；数组本身不重复，无需continue/哈希表去重；相同元素不同顺序被认为是不同结果，可以回头选择，递归实现比较简单：

暴力递归

时间条件仅允许8/16： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int result = 0;
    vector<int>temp;
    void travel(vector<int>& nums, int target){
        int sum = accumulate(temp.begin(),temp.end(),0);
        if(sum==target){
            result++;
            return;
        }
        if(sum>target)
            return;
        for(int i = 0; i<nums.size(); i++){
            temp.push_back(nums[i]);
            travel(nums,target);
            temp.pop_back();
        }        
    }

    int combinationSum4(vector<int>& nums,int target) {
        travel(nums,target);
        return result;
    }
};

动态规划

打家劫舍（从记忆化搜索dfs至常数级DP）

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：
输入：[1,2,3,1]
输出：4

参考了灵佬思路，从dfs到常数级DP的若干种方法，体现算法优化思路过程。

1. 普通dfs：通过率55/70

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int dfs(vector<int>& nums,int start){
        if(start<0)
            return 0;
        return max(dfs(nums,start-1),(dfs(nums,start-2)+nums[start]));
    }

    int rob(vector<int>& nums) {
        int result = 0;
        result += dfs(nums,nums.size()-1);    
        return result;  
    }
};

  • 时间复杂度：O(2^{n})，每个结点都能被选/不被选，当数量很高时应该是指数级。

  • 空间复杂度：O(n)，每层都调用。

2. 记忆化搜索dfs：通过率67/70

使用哈希表记录已经搜索过的总价值，例如dfs(2)一定是确定的，使用哈希表记录即可，无需再递归计算。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    unordered_map<int,int>umap;
    int dfs(vector<int>& nums,int start){
        if(start<0)
            return 0;
        if(umap[start]!=0)   //哈希表下标存在结果
            return umap[start];  //返回结果
        return umap[start]=max(dfs(nums,start-1),(dfs(nums,start-2)+nums[start]));
    }

    int rob(vector<int>& nums) {
        int result = 0;
        result += dfs(nums,nums.size()-1);    
        return result;  
    }
};

  • 时间复杂度：O(n),重复的元素不会再递归，最多递归n层，每层记录一种状态

  • 空间复杂度：仍然O(n)。

3. 动态规划（最普通想法）：通过率70/70

再优化就是完全的递推关系了，和爬楼梯很像。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size()==1)
            return nums[0];
        else if(nums.size()==2)
            return max(nums[0],nums[1]);
        //size大于等于3才需要递推：
        vector<int>dp(nums.size());
        dp[0] = nums[0];  //
        dp[1] = max(nums[0],nums[1]);
        for(int i=2; i<nums.size(); i++){
            dp[i] = max(dp[i-1],dp[i-2]+nums[i]);  //前一级子问题，或者当级+前两级子问题
        }
        return dp[nums.size()-1];

    }
};

  • 时间复杂度、空间复杂度：均为O(n)

4. 常数空间动态规划（吹毛求疵）

只需要当前元素、前一级元素、前二级元素即可，可以3个数组空间之间表示，O(1)空间复杂度。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size()==1)
            return nums[0];
        else if(nums.size()==2)
            return max(nums[0],nums[1]);
        vector<int>dp(3);  //只需要三个位置
        dp[0] = nums[0];
        dp[1] = max(nums[0],nums[1]);
        for(int i=2; i<nums.size(); i++){
            dp[2] = max(dp[1],dp[0]+nums[i]); 
            dp[0] = dp[1];   //更新梯级
            dp[1] = dp[2];
        }
        return dp[2];
    }
};

打家劫舍 II

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

example:输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

问题分析：唯一的不同是不同同时光顾1号和最后一号，需要普通打家劫舍逻辑（上题）+坐标选择。分类情况可以按size奇偶分类，实际上最后可以分成两类，两类中都各自包含奇偶情况，不会重叠。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int rob_normal(vector<int>&nums, int st,int end){ //st——end下标
        if(end-st==0)  //1个元素
            return nums[st];
        if(end-st==1)  //2个元素
            return max(nums[st],nums[st+1]);
        vector<int>dp(3); //3个及以上
        dp[0] = nums[st];
        dp[1] =max(nums[st],nums[st+1]);
        for(int i= st+2; i<=end; i++){
            dp[2] = max(dp[1],dp[0]+nums[i]);
            dp[0] = dp[1];
            dp[1] = dp[2];
        }
        return dp[2];
    }

    int rob(vector<int>& nums) {
        int n = nums.size();
        if(n==1)
            return nums[0];
        if(n==2)
            return max(nums[0],nums[1]);
        int result1 = rob_normal(nums,0,n-2);  //去除最后一个元素
        int result2 = rob_normal(nums,1,n-1);  //去除第一个元素
        return max(result1,result2); //两种方法不会重叠
    }
};

打家劫舍 III

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。 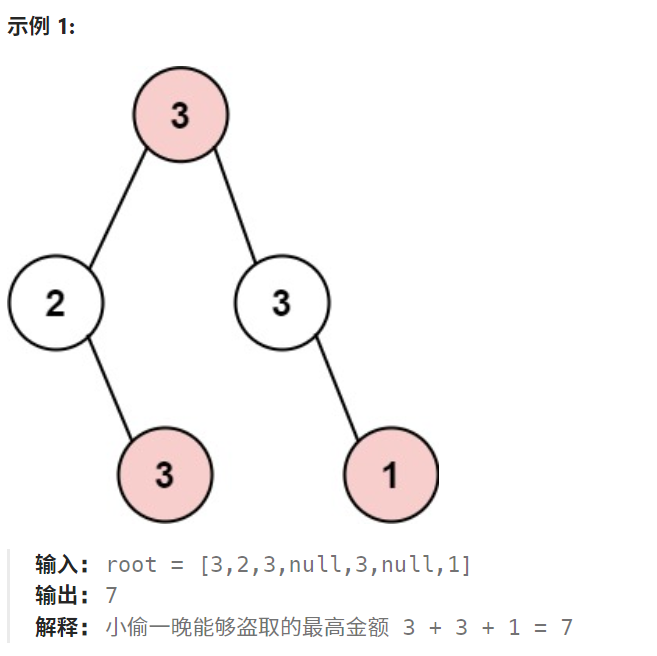示意图

普通dfs递归搜索：通过率122/124。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int dfs(TreeNode* root){
        if(root==nullptr)
            return 0;
        if(root->left==nullptr&&root->right==nullptr)
            return root->val;
        int temp1 = root->val;
        if(root->left)
            temp1 += dfs(root->left->left)+dfs(root->left->right);
        if(root->right)
            temp1 += dfs(root->right->left)+dfs(root->right->right);
        int temp2 = dfs(root->left)+dfs(root->right);
        return max(temp1,temp2);
    }

    int rob(TreeNode* root) {
        int result = 0;
        result +=dfs(root);
        return result;
    }
};

记忆化搜索dfs：时间复杂度、空间复杂度超70%水平

新增哈希表直接记录结点值，无需递归，能够高效剪枝，哈希表能直接按结点记录，不用考虑编序号问题了。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    unordered_map<TreeNode*,int>umap;
    int dfs(TreeNode* root){
        if(root==nullptr)
            return 0;
        //叶子节点，之间返回节点值
        if(root->left==nullptr&&root->right==nullptr)
            return root->val;
        if(umap[root]!=0)   //检查哈希表
            return umap[root];
        //偷父结点+下两个层的结点
        int temp1 = root->val;
        if(root->left)
            temp1 += dfs(root->left->left)+dfs(root->left->right);
        if(root->right)
            temp1 += dfs(root->right->left)+dfs(root->right->right);
        //偷子结点
        int temp2 = dfs(root->left)+dfs(root->right);
        return umap[root] = max(temp1,temp2);  //哈希表赋值
    }

    int rob(TreeNode* root) {
        int result = 0;
        result +=dfs(root);
        return result;
    }
};

回文子串

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

exampel:输入：s = "aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

动态规划算法

定义dp数组：dp[i][j] = true 表示区间[i,j]是一个回文子串，所以对dp数组：

  • i==j时，dp[i][j] = true，对角线必然为true，因为自身一个字符肯定是回文子串；例如"aaa"的三个字母自身

  • j-i==1时，dp[i][j] = true；前后相邻字符一定是回文子串，例如"aabbge"中的aa和bb；（注意使用不回头遍历）

这就是dp数组的基本盘，判断三个字符是否回文，例如"aabac"，此时知道dp[2][2] = true，即b本身回文，那么判断dp[1][3]只要s[1]==s[3]，aba回文，说明dp[1][3]==true，那么下一步就是判断dp[0][4]是否回文；最重要的点是，每次判断dp[i][j]，必然先判断dp[i+1][j-1]，说明二维数组遍历顺序应该是从下往上、从左往右。i==j和j-i==1设置时可以不遵循这个，自己进行初始化分开写，但是为了降低复杂度，可以一并更新。（这个在回文子串、回文序列中很重要，尤其是一维化滚动数组时。

另外的写法从上往下、从右往左也可以，但是没有必要深究了。

因此给定长度n字符串，动态规划的dp数组就是构建n*n的二维数组，根据上面三种方法计算出true的数目就是回文子串的数目；

如下 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int countSubstrings(string s) {
        int result = 0;
        int n = s.size();
        vector<vector<bool>>dp(n,vector<bool>(n));
        
        for(int i=s.size()-1; i>=0; i--){  //从下往上更新，先更新dp[i+1][j-1]
            for(int j=i; j<s.size(); j++){  //不回头遍历
                if(s[i]==s[j]&&j-i<=1){  //相邻两个字符或字符自身一个必然是回文子串
                    dp[i][j] = true;
                    result++;
                }
                if(s[i]==s[j]&&j-i>1&&dp[i+1][j-1]==true){  //a或aba是回文子串，babab才是回文子串
                    result++;
                    dp[i][j] = true;
                }
            }
        }

        return result;
    }
};

最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

动态规划

一种方法是利用《回文子串》中的dp数组，找到最大区间j-i即可： 

1
2
3
4
5
6
7
8
9
10
11
12
//dp构造见上一题《回文子串》，此处略
    int cur = -1;
    int max_len = -1;
    for(int i=0; i<n; i++){
        for(int j=i; j<n; j++){
            if(dp[i][j]==true&&j-i+1>max_len){  //字符串[i,j]区间构成最长回文子串
                max_len = j-i+1;   //区间长度
                cur = i;  //区间起点
            }
        }
    }
    return cur==-1?"":s.substr(cur,max_len);   //返回最长回文子串

最长回文子序列

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

example:输入：s = "bbbab" 输出：4 解释：一个可能的最长回文子序列为 "bbbb" 。

二维动态规划

回文子序列意味着不要求子串是连续的，因此实现的特性是遇到不相等的字符串，应该“继承”前后字符串的最大回文序列长度：仍然定义dp[i][j]代表字符串区间[i,j]的最大回文序列长度。

  • 初始时，对角线代表字符自身的回文长度，恒为1；

  • 两个字符时，更不更新都可以，因为此情况包含在其他两种情况；

  • 当多个字符时（两个及以上），例如"bb"，中间元素看成空，那么dp[0][1] = 0+2;如果是三个字符，例如bab，dp[1][1]=1，dp[0][2]=1+2=3；因此只要遇到非对角线元素（i!=j），且字符相等，就应该扩展它的最大回文序列长度。

  • 当遇到非对角线元素，且字符不等时，例如"cbaba"，其中dp[1][3] = 3，c和a不等，说明c、a不可能同时是最长回文序列的成员，因此dp[0][4]一定是和dp[0][3]或者dp[1][4]结果相同的，同理dp[0][3]包含了c和b，c、b也不可能同时在最长回文序列，因此dp[0][3]取决于dp[1][3]或者dp[0][2]，最后递推dp[i][j] = max(dp[i+1][j],dp[i][j-1]);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        vector<vector<int>>dp(n,vector<int>(n));
        
        for(int i=s.size()-1; i>=0; i--){
            for(int j=i; j<s.size(); j++){
                if(i==j)  //对角线
                    dp[i][j] = 1;
                else if(s[i]==s[j]) //非对角线，且元素相等
                    dp[i][j] = dp[i+1][j-1] + 2;
                else     //非对角线，且元素不等
                    dp[i][j] = max(dp[i+1][j],dp[i][j-1]);
            }
        }

        return dp[0][n-1];
    }
};

最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

example:输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4

记忆化搜索

从元素i开始向前，找前一个小元素，递归到该小元素，直到递归找到该序列最开始的小元素，递归结果为1，回溯回去即可获得元素i之前的递增子序列长度，最后计算i=1到末尾的，去最大长度的子序列结果即可。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    unordered_map<int,int>umap;
    int dfs(vector<int>& nums,int i){
        int len = 0;
        if(umap[i]!=0)
            return umap[i];
        for(int j=i-1; j>=0; j--){//也可0到i-1
            if(nums[j]<nums[i])  //找元素nums[i]前一个小元素
                len = max(len,dfs(nums,j));  //找到，长度递归到j或者j之前小元素的子序列较长值
        }
        return umap[i]=len+1;  //子序列长度+1
    }
    int lengthOfLIS(vector<int>& nums) {
        int result = 0;
        for(int i=0; i<nums.size(); i++){  //计算0~i元素的最长子序列
            result = max(result,dfs(nums,i));
        }
        return result;
    }
};

动态规划

记忆化搜索的递归用数组递推表示，即得动态规划，以下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int>dp(n);
        for(int i=0; i<nums.size(); i++){
            for(int j=i-1; j>=0; j--){
                if(nums[j]<nums[i])
                    dp[i] = max(dp[i],dp[j]); //len = max(len,dfs(nums,j));
            }
            dp[i]++;
        }
        
        int result = 0;
        for(int i:dp){
            result = max(result,i);
        }
        return result;
    }
};

最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。 两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

example:输入：text1 = "abcde", text2 = "ace"
输出：3
解释：最长公共子序列是 "ace" ，它的长度为 3 。

递归算法：通过16/47

加入记忆化内存超限，最终都是为了推DP方法，递归关系如下：

从两个字符串末尾开始选，如果text1[i]==text2[j]，说明i和j都是子序列的一部分，子长度=前面子长度+1；若text1[i]！=text2[j]，说明i、j不共存，子问题为其中一个序列的最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int dfs(string text1,string text2,int i,int j){
        if(i<0||j<0)
            return 0;
        if(text1[i]==text2[j])  //存在相同字符
            return dfs(text1,text2,i-1,j-1)+1; //子问题 + 长度1
        else //字符不相同
            return max(dfs(text1,text2,i-1,j),dfs(text1,text2,i,j-1)); //子问题是不选i或者不选j项
    }

    int longestCommonSubsequence(string text1, string text2) {
        int result = 0;
        result += dfs(text1,text2,text1.size()-1,text2.size()-1);
        return result;
    }
};

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m = text1.size();
        int n = text2.size();
        vector<vector<int>>dp(m+1,vector<int>(n+1)); //+1是为了不越界
        //递推关系左到右、上到下，和遍历顺序对应
        for(int i=0; i<m; i++){
            for(int j=0; j<n; j++){
                if(text1[i]==text2[j])
                    dp[i+1][j+1] = dp[i][j] + 1;  //dfs(text1,text2,i-1,j-1)+1;
                else   
                    dp[i+1][j+1] = max(dp[i+1][j],dp[i][j+1]); //max(dfs(text1,text2,i-1,j),dfs(text1,text2,i,j-1));
            }
        }
        return dp[m][n];
    }
};

最长递增子串

如果问题不是子序列，而是递增的子串，DP和贪心算法比较简单 ##### 贪心算法 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int count = 1;
        int result =1;  //单个字符算递增子串长度1
        for(int i=1; i<nums.size(); i++){
            if(nums[i]>nums[i-1]){
                count ++;
                result = max(count,result); //计算最大值
            }
            else
                count = 1;  //如果遇到逆序，从头计算
        }
        return result;
    }
};

最长重复子数组

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7] 输出：3 解释：长度最长的公共子数组是 [3,2,1] 。

本题使用动态规划是最简单的，直接使用卡哥给出的递推公式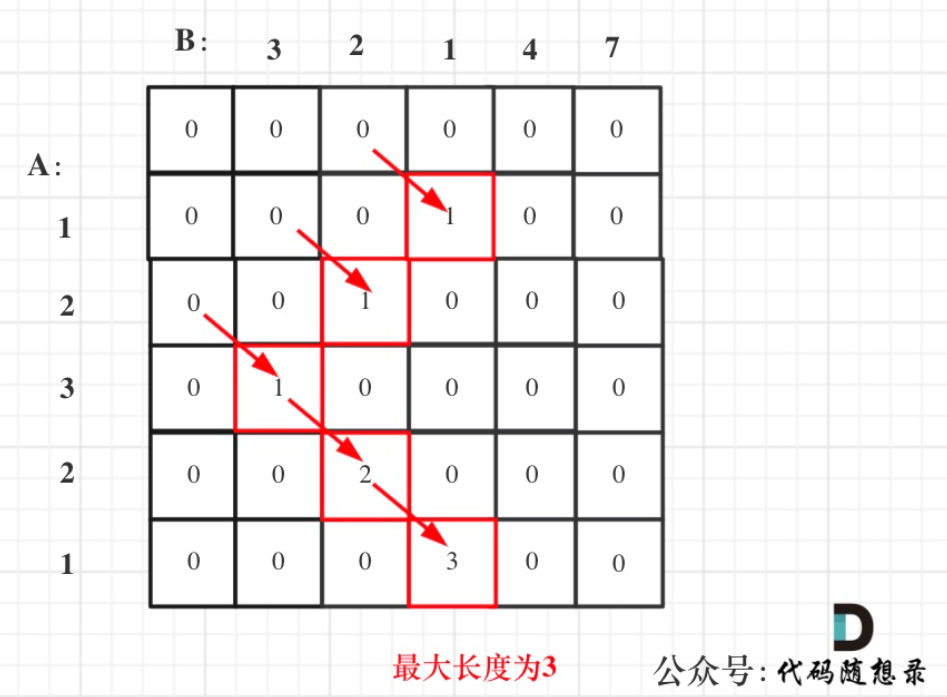： 最长重复子数组dp 当左上角元素相等，那么右下角累计1，如果左上角归零，那么重新累积即可，结果就是二维数组的最大值。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size();
        int n = nums2.size();
        vector<vector<int>>dp(m+1,vector<int>(n+1));
        int result = 0;
        for(int i=1; i<=m; i++){
            for(int j=1; j<=n; j++){
                if(nums1[i-1]==nums2[j-1])  //左上角相等
                    dp[i][j] = dp[i-1][j-1]+1;  //累积
                result = max(result,dp[i][j]);
            }
        }
        return result;
    }
};

编辑距离

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

  • 插入一个字符
  • 删除一个字符
  • 替换一个字符

example:输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

递归算法

问题分析：主要窍门是将三种操作抽象，从末尾开始：
- 当word1[i]==word2[j]，说明i、j共存，无需操作，因此其操作数同子问题dfs(i-1,j-1);

  • 当word1[i]!=word2[j]，将word1转换word2，有可能需要三种操作：
  1. 插入操作：插入后子问题是dfs(i,j-1)，相当于插入一个值，抵消了j。
  2. 删除操作：删除后子问题是dfs(i-1,j)，相当于删除word1的第i个值，无需比较i。
  3. 替换操作：替换后子问题是dfs(i-1,j-1)，替换相当于二者直接匹配，比较字符直接看前面字符。

选择这三种操作数最小值，并且+1作为字符起始——当前位置转换需要操作数。以下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    //将word1转化成word2
    int dfs(string word1,string word2,int i,int j){
        if(i<0)  //i没了，j还有：在word2插入剩下字符
            return j+1;   //下标+1才是数量
        if(j<0) //j没了,i还有：删除work1剩下字符
            return i+1;
        if(word1[i]==word2[j]) //相等
            return dfs(word1,word2,i-1,j-1); //无需操作
        else//不相等：对应插入、删除、替换
            return min(dfs(word1,word2,i,j-1),min(dfs(word1,word2,i-1,j),dfs(word1,word2,i-1,j-1)))+1;
    }

    int minDistance(string word1, string word2) {
        int result = 0;
        result += dfs(word1,word2,word1.size()-1,word2.size()-1);
        return result;
    }
};

动态规划

将递归换成数组，并且调整，注意不要遗漏初始化条件，i<0时(实际上就是i==-1，dp[-1][j]=j+1)，因此将i、j换成i+1、j+1后，对应的就是第0行，dp[0][j] = j（注意：为什么不是dp[0][j]=j+1，首先因为j+1代替了j，因此换成j，而坐标的j已经体现在范围变化中了，所以就不用换，而i+1就体现在-1变成0.），列初始化同理。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    //将word1转化成word2
    int dfs(string word1,string word2,int i,int j){
        if(i<0)  //i没了，j还有：在word2插入剩下字符
            return j+1;
        if(j<0) //j没了,i还有：删除work1剩下字符
            return i+1;
        if(word1[i]==word2[j])
            return dfs(word1,word2,i-1,j-1);
        else
            return min(dfs(word1,word2,i,j-1),min(dfs(word1,word2,i-1,j),dfs(word1,word2,i-1,j-1)))+1;
    }

    int minDistance(string word1, string word2) {
        int m = word1.size();
        int n = word2.size();
        vector<vector<int>>dp(m+1,vector<int>(n+1));
        
        for(int i=0; i<=m; i++){
            dp[i][0] = i;
        }

        for(int j=0; j<=n; j++){
            dp[0][j] = j;
        }
        
        for(int i=0; i<m; i++){
            for(int j=0; j<n; j++){
                if(word1[i]==word2[j])
                    dp[i+1][j+1] = dp[i][j];
                else    
                    dp[i+1][j+1] = min(dp[i+1][j],min(dp[i][j+1],dp[i][j]))+1;
            }
        }
        return dp[m][n];
    }
};

图论

1. 所有可达路径

给定一个有 n 个节点的有向无环图，节点编号从 1 到 n。请编写一个函数，找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。

example:
输入:
5 5
1 3
3 5
1 2
2 4
4 5
输出:
1 3 5
1 2 4 5

回看我的数据结构第三篇文章，实际上那种标记——访问写法还比较稚嫩，carl的这个写法更具有dfs的通用性，因为这种写法既可以找到图的某两个点的所有路径，也可以找到首先走的第一条路径（改成bool类型+return true即可）。直接看代码即可： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <vector>
using namespace std;

class Solution{
public:
    vector<int>temp;
    vector<vector<int>>result;
    void dfs(vector<vector<int>>&db_Array,int start,int end){
        if(start == end){  //当前遍历的点start就是终点，记录一个路径
            result.push_back(temp);
            return;
        }
        for(int i=0; i<=end; i++ ){  //每次递归从0遍历到end，看是否有路径
            if(db_Array[start][i]==1){ //存在有向图路径
                temp.push_back(i);  //决策
                dfs(db_Array,i,end); //递归下一个点
                temp.pop_back();         
            }
        }
    }
};

int main(){
    int m,n; //边数、节点数
    cin>>n>>m;
        
    vector<vector<int>> db_Array(n+1,vector<int>(n+1)); //因为是遍历到n，所以0到n都需要记录
    int i,j;

    while(m--){  //读取输入
        cin>>i>>j;
        db_Array[i][j] = 1;
    }
    //调用解决
    Solution mySolution;
    mySolution.temp.push_back(1);
    mySolution.dfs(db_Array,1,n);
    
    if(mySolution.result.size()==0){  //面对测试用例，没有result输出-1
        cout << -1<<endl;
        return 0;
    }
    
    //打印result结果，二维数组通过cout变成行打印
    for(int i=0; i<mySolution.result.size();i++){ //i是数组
        for(int j=0; j<mySolution.result[i].size()-1; j++){ //打印前面的数+空格
            cout << mySolution.result[i][j] <<" ";
        }
        cout <<mySolution.result[i][mySolution.result[i].size()-1]<<endl; //最后一个数不能加空格，分开打印
    }
    
    return 0;
}

2. 岛屿数量

给定一个由 1（陆地）和 0（水）组成的矩阵，你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成，并且四周都是水域。你可以假设矩阵外均被水包围。

输入描述：第一行包含两个整数 N, M，表示矩阵的行数和列数。后续 N 行，每行包含 M 个数字，数字为 1 或者 0。

输出描述：输出一个整数，表示岛屿的数量。如果不存在岛屿，则输出 0。

example:
输入：
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出：3

问题分析：找出数组中“一块一块”的小元素块。

深度搜索方法dfs

岛屿问题像是一种区域生长问题，虽然本题使用了递归，但是和我们做过的回溯算法不同，本地遍历每个点，尝试其上下左右是否有路径，找到该区域的生长边缘，根本不需要回溯回去，所以没有那种“决策——取消决策的模板”，当该区域已经遍历完毕了，周围要么越界、是海的区域、遍历过的区域，dfs就无法递归下去，这时就需要依靠main函数的数组循环寻找新的区域生长起点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <iostream>
#include <vector>
using namespace std;

class Solution{
public:
    int M,N;  //n行m列
    int dir[4][2]={  //方向数组
        0,1,  //y加1，向右
        1,0,  //x加1，向下
        -1,0, //x减1，向上
        0,-1  //y减一，向左
    };

    Solution(int M,int N):M(M),N(N){}
    void dfs(vector<vector<int>>&db_Array,vector<vector<bool>>&visited,int x,int y){
        visited[x][y] = true;  //标记
        for(int i=0; i<4; i++){
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            if(nextx<0||nexty<0||nextx>=N||nexty>=M)//越界，跳过
                continue;
            if(visited[nextx][nexty]==true||db_Array[nextx][nexty]==0)//遇到海或者位置已经走过了
                continue;
            dfs(db_Array,visited,nextx,nexty);  //递归下一点
        }
    }
};

int main(){
    int m,n; //n行m列
    cin>>n>>m;
    
    vector<vector<int>>db_Array(n,vector<int>(m));
        
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
            cin>>db_Array[i][j];
        }
    }
    
    Solution mySolution(m,n); //n行m列
    
    vector<vector<bool>>visited(n,vector<bool>(m,false));
    int result = 0;
    
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){  //该双层循环用于寻找新的区域生长起点
            if(db_Array[i][j]==1&&visited[i][j]==false){ //找到一个区域生长起点
                result++;   //记录起点
                mySolution.dfs(db_Array,visited,i,j); //生长区域访问
            }
        }
    }
    
    cout<<result<<endl;  //输出所有起点数，就是生长区域数。
    return 0;   
}

广度搜索方法bfs

深度搜索的方法是从起点开始，递归标记一个区域，广度搜索的方法，是沿着中心点一圈一圈地向外搜索，意味着遍历到下一层，就需要一种结构来存储该层的结点，逐个处理该层的结点，和层序遍历一样，这种结构常常是满足FIFO的队列结构。因为深度搜索的标记是通过递归标记x、y（某行、某列），广度的要同时记录一层的x、y，就需要pair的辅助。其他逻辑是大致相同的；

注意一个细节：深搜可以先递归、再标记，也可以先标记再递归，而队列bfs只能先标记再循环，否则会出现超时！！ 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

class Solution{
public:
    int M,N;
    int dir[4][2]={
        0,1,    //y加1，向下
        1,0,    //x加1，向右
        -1,0,   //x减1，向左
        0,-1    //y减一，向上
    };

    Solution(int M,int N):M(M),N(N){};
    void bfs(vector<vector<int>>& db_Array,vector<vector<bool>>& visited,int x,int y){
        queue<pair<int,int>> que;
        que.push({x,y});  //第一次的区域生长位置
        while(!que.empty()){  //逐层遍历处理
            pair<int,int>pair_tmp = que.front();  //逐层元素
            que.pop();
            for(int i=0;i<4;i++){
                int nextx = pair_tmp.first+dir[i][0];  //每一层的下一步，同dfs逻辑
                int nexty = pair_tmp.second+dir[i][1];
                if(nextx<0||nextx>=N||nexty<0||nexty>=M)
                    continue;
                if(db_Array[nextx][nexty]==0||visited[nextx][nexty]==true)
                    continue;
                que.push({nextx,nexty});  //满足条件作为下一层要处理的队列结点
                visited[nextx][nexty] = true;  //必须先标记，否则会超时
            }
        }
        
    }

};

int main(){
    int m,n; //n行m列
    cin>>n>>m;
    
    vector<vector<int>>db_Array(n,vector<int>(m));
        
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
            cin>>db_Array[i][j];
        }
    }
    
    Solution mySolution(m,n); //n行m列
    
    vector<vector<bool>>visited(n,vector<bool>(m,false));
    int result=0;
    for(int i=0; i<n; i++){  //双层循环寻找新区域生长，同dfs逻辑
        for(int j=0; j<m; j++){
            if(db_Array[i][j]==1&&visited[i][j]==false){
               result++;
               visited[i][j] = true;
               mySolution.bfs(db_Array,visited,i,j);
            }
        }
    }
    
    cout<< result <<endl;
    return 0;
}

3. 岛屿的最大面积

给定一个由 1（陆地）和 0（水）组成的矩阵，计算岛屿的最大面积。岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿由水平方向或垂直方向上相邻的陆地连接而成，并且四周都是水域。你可以假设矩阵外均被水包围。

example:
输入：
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出：4

问题分析：这应该是作者出上一题时想到的，因为上一题的result放在main函数，只计算了区域的数量，即岛屿计数，result还可以放在类中，这时候就变成面积计数了，只要每次记下递归的数量，就可以知道面积大小了，在main中取最大值即可。其他逻辑和上题是一样的：

深度搜索dfs方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <iostream>
#include <vector>
using namespace std;

class Solution{
public:
    int M,N;
    int count=0;
    int dir[4][2]={  //方向数组
        0,1,  //y加1，向右
        1,0,  //x加1，向下
        -1,0, //x减1，向上
        0,-1  //y减一，向左
    };
    Solution(int M,int N):M(M),N(N){}
    void dfs(vector<vector<int>>& db_Array,vector<vector<bool>>& visited,int x,int y){
        for(int i=0; i<4; i++){  //四次循环分别代表向上、向下、向左、向右
            int nextx = x + dir[i][0];  
            int nexty = y + dir[i][1];  
            if(nextx<0||nextx>=N||nexty<0||nexty>=M) //越界，跳过
                continue;
            if(db_Array[nextx][nexty]==0||visited[nextx][nexty]==true) //遇到海或者位置已经走过了
                continue;
            visited[nextx][nexty] = true; //标记
            dfs(db_Array,visited,nextx,nexty); //递归下一点
            count++;
        }
    }
};


int main(){
    int m,n; //n行m列
    cin>>n>>m;
    
    vector<vector<int>>db_Array(n,vector<int>(m));
        
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
            cin>>db_Array[i][j];
        }
    }
    
    Solution mySolution(m,n); //n行m列
    
    vector<vector<bool>>visited(n,vector<bool>(m,false));
    int result=0;
    
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){  //该双层循环用于寻找新的区域生长起点
            if(db_Array[i][j]==1&&visited[i][j]==false){ //找到一个区域生长起点
                mySolution.count =1;
                visited[i][j] = true; //起点访问
                mySolution.dfs(db_Array,visited,i,j); //生长区域访问
                result = max(result,mySolution.count);
            }
        }
    }
    
    cout<<result<<endl;  //输出所有起点数，就是生长区域数。
    return 0;   
}

广度搜索dfs方法

层序遍历的方法仍然能够找到所有符合条件的陆地，双层循环仍然需要重新找到生长区域，因此一样的方法找到答案： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

class Solution{
public:
    int M,N;
    int count=0;
    int dir[4][2]={  //方向数组
        0,1,  //y加1，向右
        1,0,  //x加1，向下
        -1,0, //x减1，向上
        0,-1  //y减一，向左
    };

    Solution(int M,int N):M(M),N(N){};
    void bfs(vector<vector<int>>& db_Array,vector<vector<bool>>& visited,int x,int y){
        queue<pair<int,int>> que;
        que.push({x,y});  //第一次的区域生长位置
        while(!que.empty()){  //逐层遍历处理
            pair<int,int>pair_tmp = que.front();  //逐层元素
            que.pop();
            for(int i=0;i<4;i++){
                int nextx = pair_tmp.first+dir[i][0];  //每一层的下一步，同dfs逻辑
                int nexty = pair_tmp.second+dir[i][1];
                if(nextx<0||nextx>=N||nexty<0||nexty>=M)
                    continue;
                if(db_Array[nextx][nexty]==0||visited[nextx][nexty]==true)
                    continue;
                que.push({nextx,nexty});  //满足条件作为下一层要处理的队列结点
                visited[nextx][nexty] = true;  //必须先标记，否则会超时
                count++;  //一个结点入队，面积就要计数
            }
        }
        
    }

};

int main(){
    int m,n; //n行m列
    cin>>n>>m;
    
    vector<vector<int>>db_Array(n,vector<int>(m));
        
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
            cin>>db_Array[i][j];
        }
    }
    
    Solution mySolution(m,n); //n行m列
    
    vector<vector<bool>>visited(n,vector<bool>(m,false));
    int result =0;
    for(int i=0; i<n; i++){  //双层循环寻找新区域生长，同dfs逻辑
        for(int j=0; j<m; j++){
            if(db_Array[i][j]==1&&visited[i][j]==false){
               mySolution.count=1;
               visited[i][j] = true;
               mySolution.bfs(db_Array,visited,i,j);
               result =max(mySolution.count,result);
            }
        }
    }
    
    cout<< result <<endl;
    return 0;
}

4. 孤岛的总面积

给定一个由 1（陆地）和 0（水）组成的矩阵，岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域，且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。

现在你需要计算所有孤岛的总面积，岛屿面积的计算方式为组成岛屿的陆地的总数。

输入描述 第一行包含两个整数 N, M，表示矩阵的行数和列数。之后 N 行，每行包含 M 个数字，数字为 1 或者 0。 输出描述 输出一个整数，表示所有孤岛的总面积，如果不存在孤岛，则输出 0。

example:
输入：
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出：1

问题分析：增加一个判断孤岛逻辑就好了，遇到越界时之前是直接continue，现在可以先使用flag，如果flag=1时代表该位置递归越界，代表一定是边缘的区域，每次for循环重新寻找区域起点时记得先将flag复位。

深度搜索方法dfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <iostream>
#include <vector>
using namespace std;

class Solution{
public:
    int M,N;
    int count=0;
    int flag =0;
    int dir[4][2]={  //方向数组
        0,1,  //y加1，向右
        1,0,  //x加1，向下
        -1,0, //x减1，向上
        0,-1  //y减一，向左
    };
    Solution(int M,int N):M(M),N(N){};
    void dfs(vector<vector<int>>& db_Array,vector<vector<bool>>& visited,int x,int y){
        for(int i=0; i<4; i++){  //四次循环分别代表向上、向下、向左、向右
            int nextx = x + dir[i][0];  
            int nexty = y + dir[i][1];  
            if(nextx<0||nextx>=N||nexty<0||nexty>=M){ //能递归到边界，说明不是孤岛
                flag =1;
                continue;
            } 
            if(db_Array[nextx][nexty]==0||visited[nextx][nexty]==true) //遇到海或者位置已经走过了
                continue;
            visited[nextx][nexty] = true; //标记
            dfs(db_Array,visited,nextx,nexty); //递归下一点
            count++;
        }
    }
};


int main(){
    int m,n; //n行m列
    cin>>n>>m;
    
    vector<vector<int>>db_Array(n,vector<int>(m));
        
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
            cin>>db_Array[i][j];
        }
    }
    
    Solution mySolution(m,n); //n行m列
    
    vector<vector<bool>>visited(n,vector<bool>(m,false));
    int result=0;
    
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){  //该双层循环用于寻找新的区域生长起点
            if(db_Array[i][j]==1&&visited[i][j]==false){ //找到一个区域生长起点
                mySolution.count =1;
                mySolution.flag =0;  //重新置位
                visited[i][j] = true; //起点访问
                mySolution.dfs(db_Array,visited,i,j); //生长区域访问
                if(mySolution.flag==0)
                    result += mySolution.count;  //不是边缘，面积相加
            }
        }
    }
    
    cout<<result<<endl;  //输出所有起点数，就是生长区域数。
    return 0;   
}

广度搜索方法bfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

class Solution{
public:
    int M,N;
    int count=0;
    int flag =0;
    int dir[4][2]={  //方向数组
        0,1,  //y加1，向右
        1,0,  //x加1，向下
        -1,0, //x减1，向上
        0,-1  //y减一，向左
    };

    Solution(int M,int N):M(M),N(N){};
    void bfs(vector<vector<int>>& db_Array,vector<vector<bool>>& visited,int x,int y){
        queue<pair<int,int>> que;
        que.push({x,y});  //第一次的区域生长位置
        while(!que.empty()){  //逐层遍历处理
            pair<int,int>pair_tmp = que.front();  //逐层元素
            que.pop();
            for(int i=0;i<4;i++){
                int nextx = pair_tmp.first+dir[i][0];  //每一层的下一步，同dfs逻辑
                int nexty = pair_tmp.second+dir[i][1];
                if(nextx<0||nextx>=N||nexty<0||nexty>=M){
                    flag =1;  //越界，代表该区域接触边缘
                    continue;
                }
                    
                if(db_Array[nextx][nexty]==0||visited[nextx][nexty]==true)
                    continue;
                que.push({nextx,nexty});  //满足条件作为下一层要处理的队列结点
                visited[nextx][nexty] = true;
                count++;  //一个结点入队，面积就要计数
            }
        }
        
    }

};

int main(){
    int m,n; //n行m列
    cin>>n>>m;
    
    vector<vector<int>>db_Array(n,vector<int>(m));
        
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
            cin>>db_Array[i][j];
        }
    }
    
    Solution mySolution(m,n); //n行m列
    
    vector<vector<bool>>visited(n,vector<bool>(m,false));
    int result =0;
    for(int i=0; i<n; i++){  //双层循环寻找新区域生长，同dfs逻辑
        for(int j=0; j<m; j++){
            if(db_Array[i][j]==1&&visited[i][j]==false){
               mySolution.count=1;
               mySolution.flag =0;
               visited[i][j] = true;
               mySolution.bfs(db_Array,visited,i,j);
               if(mySolution.flag==0) //不接触边缘才加面积
                result +=mySolution.count;
            }
        }
    }
    
    cout<< result <<endl;
    return 0;
}

5. 沉没孤岛

给定一个由 1（陆地）和 0（水）组成的矩阵，岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域，且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。

现在你需要将所有孤岛“沉没”，即将孤岛中的所有陆地单元格（1）转变为水域单元格（0）。

输入描述 第一行包含两个整数 N, M，表示矩阵的行数和列数。

之后 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。

输出描述 输出将孤岛“沉没”之后的岛屿矩阵。 注意：每个元素后面都有一个空格

输入:
4 5
1 1 0 0
1 1 0 0
0 0 1 0
0 0 0 1
输出:
1 1 0 0
1 1 0 0
0 0 0 0
0 0 0 1

问题分析：上一题我们判断了孤岛，现在除了判断孤岛，还需要将孤岛的"1"变成“0”，要知道递归函数并没有返回二维函数结果，我们很容易找到孤岛，但是不知道哪些递归坐标是属于孤岛；在函数里回溯也是不可能的，因为递归完成前，我们也不能确切知道当前元素是否属于孤岛；但仔细一想，递归完成后除了通过flag辨别孤岛，还知道这个孤岛的区域生长起点（i，j），因此递归这个(i,j)就能找到所有孤岛点，再递归一次将其置0，通过新的travel函数实现，以下：

深度搜索方法dfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <iostream>
#include <vector>
using namespace std;

class Solution{
public:
    int M,N;
    int count=0;
    int flag =0;
    int dir[4][2]={  //方向数组
        0,1,  //y加1，向右
        1,0,  //x加1，向下
        -1,0, //x减1，向上
        0,-1  //y减一，向左
    };
    Solution(int M,int N):M(M),N(N){};
    void dfs(vector<vector<int>>& db_Array,vector<vector<bool>>& visited,int x,int y){
        for(int i=0; i<4; i++){  //四次循环分别代表向上、向下、向左、向右
            int nextx = x + dir[i][0];  
            int nexty = y + dir[i][1];  
            if(nextx<0||nextx>=N||nexty<0||nexty>=M){
                flag =1;  //同上题，非孤岛flag置1
                continue;
            } 
            if(db_Array[nextx][nexty]==0||visited[nextx][nexty]==true) //遇到海或者位置已经走过了
                continue;
            visited[nextx][nexty] = true; //标记
            dfs(db_Array,visited,nextx,nexty); //递归下一点
            count++;
        }
    }
    
    //新增travel负责将孤岛元素置0
    void travel(vector<vector<int>>& db_Array,vector<vector<bool>>& travel_visited,int x,int y){
        for(int i=0; i<4; i++){
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            if(nextx<0||nextx>=N||nexty<0||nexty>=M)
                continue;
            if(db_Array[nextx][nexty]==0||travel_visited[nextx][nexty]==true)
                continue;
            db_Array[nextx][nexty] = 0; //置0
            travel_visited[nextx][nexty] = true; //标志访问
            travel(db_Array,travel_visited,nextx,nexty); //递归置0
        }
    }
};

int main(){
    int m,n; //n行m列
    cin>>n>>m;
    
    vector<vector<int>>db_Array(n,vector<int>(m));
        
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
            cin>>db_Array[i][j];
        }
    }
    
    Solution mySolution(m,n); //n行m列
    
    vector<vector<bool>>visited(n,vector<bool>(m,false));

    vector<vector<bool>>travel_visited(n,vector<bool>(m,false));  
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){  //该双层循环用于寻找新的区域生长起点
            if(db_Array[i][j]==1&&visited[i][j]==false){ //找到一个区域生长起点
                mySolution.count =1;
                mySolution.flag =0;  //重新置位
                visited[i][j] = true; //起点访问
                mySolution.dfs(db_Array,visited,i,j); //生长区域访问
                if(mySolution.flag==0){  //递归完没有越界，说明是孤岛
                    travel_visited[i][j] = true;  //标记起点
                    db_Array[i][j] = 0; //孤岛起点置零，沉没
                    mySolution.travel(db_Array,travel_visited,i,j);  //递归置0
                }
            }
        }
    }
    
    //输出新的二维数组结果
    for(int i=0; i<n; i++){
        for(int j=0; j<m-1; j++){
            cout<<db_Array[i][j]<<" ";
        }
        cout<<db_Array[i][m-1]<<endl;
    }
    return 0;   
}

广度搜索方法bfs

广度和深度的修改逻辑是基本一致的： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

class Solution{
public:
    int M,N;
    int count=0;
    int flag =0;
    int dir[4][2]={  //方向数组
        0,1,  //y加1，向右
        1,0,  //x加1，向下
        -1,0, //x减1，向上
        0,-1  //y减一，向左
    };

    Solution(int M,int N):M(M),N(N){};
    void bfs(vector<vector<int>>& db_Array,vector<vector<bool>>& visited,int x,int y){
        queue<pair<int,int>> que;
        que.push({x,y});  //第一次的区域生长位置
        while(!que.empty()){  //逐层遍历处理
            pair<int,int>pair_tmp = que.front();  //逐层元素
            que.pop();
            for(int i=0;i<4;i++){
                int nextx = pair_tmp.first+dir[i][0];  //每一层的下一步，同dfs逻辑
                int nexty = pair_tmp.second+dir[i][1];
                if(nextx<0||nextx>=N||nexty<0||nexty>=M){
                    flag =1;  //越界，代表该区域接触边缘
                    continue;
                }
                    
                if(db_Array[nextx][nexty]==0||visited[nextx][nexty]==true)
                    continue;
                que.push({nextx,nexty});  //满足条件作为下一层要处理的队列结点
                visited[nextx][nexty] = true;
                count++;  //一个结点入队，面积就要计数
            }
        }
        
    }
    
    void travel(vector<vector<int>>& db_Array,vector<vector<bool>>& travel_visited,int x,int y){
        for(int i=0; i<4; i++){
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            if(nextx<0||nextx>=N||nexty<0||nexty>=M)
                continue;
            if(db_Array[nextx][nexty]==0||travel_visited[nextx][nexty]==true)
                continue;
            db_Array[nextx][nexty] = 0; //置0
            travel_visited[nextx][nexty] = true; //标志访问
            travel(db_Array,travel_visited,nextx,nexty); //递归置0
        }
    }

};

int main(){
    int m,n; //n行m列
    cin>>n>>m;
    
    vector<vector<int>>db_Array(n,vector<int>(m));
        
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
            cin>>db_Array[i][j];
        }
    }
    
    Solution mySolution(m,n); //n行m列
    
    vector<vector<bool>>visited(n,vector<bool>(m,false));
    vector<vector<bool>>travel_visited(n,vector<bool>(m,false));
    for(int i=0; i<n; i++){  //双层循环寻找新区域生长，同dfs逻辑
        for(int j=0; j<m; j++){
            if(db_Array[i][j]==1&&visited[i][j]==false){
               mySolution.count=1;
               mySolution.flag =0;
               visited[i][j] = true;
               mySolution.bfs(db_Array,visited,i,j);
               if(mySolution.flag==0){
                   travel_visited[i][j] = 0;
                   db_Array[i][j] = 0;
                   mySolution.travel(db_Array,travel_visited,i,j);
               }
                
            }
        }
    }
    
    //输出新的二维数组结果
    for(int i=0; i<n; i++){
        for(int j=0; j<m-1; j++){
            cout<<db_Array[i][j]<<" ";
        }
        cout<<db_Array[i][m-1]<<endl;
    }
    return 0;
}

6. 水流问题

现有一个 N × M 的矩阵，每个单元格包含一个数值，这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界，而矩阵的右边界和下边界被视为第二组边界。

矩阵模拟了一个地形，当雨水落在上面时，水会根据地形的倾斜向低处流动，但只能从较高或等高的地点流向较低或等高并且相邻（上下左右方向）的地点。我们的目标是确定那些单元格，从这些单元格出发的水可以达到第一组边界和第二组边界。

输入描述 第一行包含两个整数 N 和 M，分别表示矩阵的行数和列数。

后续 N 行，每行包含 M 个整数，表示矩阵中的每个单元格的高度。

输出描述 输出共有多行，每行输出两个整数，用一个空格隔开，表示可达第一组边界和第二组边界的单元格的坐标，输出顺序任意。

example:输入
5 5
1 3 1 2
1 2 1 3
2 4 7 2
4 5 6 1
1 4 1 2
输出
0 4
1 3
2 2
3 0
3 1
3 2
4 0
4 1
意思是某个坐标的数能否同时到达第一、第二边界，到达第一、第二边界的经过路径的值必须小于或者等于前面的值，如果可以就记录这个坐标。

暴力超时版

直接的方法是判断某个起点的递归能否同时满足第一边界越界和第二边界越界，如果可以说明以该起点的递归是可行的，因此一共mn个元素都要进行判断，每次递归产生的路径比较是mn-1次，因此总的时间复杂度是，非常耗时。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <iostream>
#include <vector>
using namespace std;

class Solution{
public:
    int dir[4][2] = {
    -1,0,
    1,0,
    0,-1,
    0,1
    };
    int flag_up=0;  //第一边界，即左边界、上边界
    int flag_down =0; //第二边界，即右边界、下边界
    int N,M;
    Solution(int N,int M):N(N),M(M){};
    void dfs(vector<vector<int>>& dbArray,vector<vector<bool>>& visited ,int x,int y){
        for(int i=0; i<4; i++){
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];
            if(nextx<0||nexty<0){  //第一边界越界
                flag_up = 1;
                continue;
            }        
            if(nextx>=N||nexty>=M){ //第二边界越界
                flag_down = 1;
                continue;
            }
            if(dbArray[nextx][nexty]>dbArray[x][y]||visited[nextx][nexty]==true) //走过，或者不能走
                continue;
            visited[nextx][nexty] = true;  
            dfs(dbArray,visited,nextx,nexty); //递归遍历
        }
    }
    
};

int main(){
    int n,m;
    cin >>n>>m; //n行m列
    
    vector<vector<int>> dbArray(n,vector<int>(m));
    //输入
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
            cin>>dbArray[i][j];
        }
    }
    
    Solution mySolution(n,m);
    vector<pair<int,int>> result;
    for(int i=0; i<n; i++){
        for(int j=0; j<m; j++){
                vector<vector<bool>> visited(n,vector<bool>(m,false));
                mySolution.flag_down = 0;  //每次新起点，都要重置标记位
                mySolution.flag_up = 0;
                mySolution.dfs(dbArray,visited,i,j);
                if(mySolution.flag_down&&mySolution.flag_up)  //如果都能越界
                    result.push_back({i,j}); //说明该起点可行
        }
    }
    //打印结果
    for(int i=0; i<result.size(); i++){
        cout << result[i].first<<" ";
        cout<< result[i].second<<endl;
    }
    
    return 0;
}

标记法

大概是博主针对边遍历方法特意设计的题目，因为在之前的岛屿题目中原文都采用了从边开始的遍历方法，而我没有使用过，一直的思路是寻找区域生长的起点，能够解决所有的岛屿问题。

这里还是针对刚刚的算法进行优化，刚刚的问题在于每个点的递归深度都可能是mn-1，每个点都要重新递归，而实际上递归过的点完全可以不再递归，只需要在找路径时，顺便也判断这个点能否同时到达

寻找存在的路径

给定一个包含 n 个节点的无向图中，节点编号从 1 到 n （含 1 和 n ）。

你的任务是判断是否有一条从节点 source 出发到节点 destination 的路径存在。

输入描述

第一行包含两个正整数 N 和 M，N 代表节点的个数，M 代表边的个数。

后续 M 行，每行两个正整数 s 和 t，代表从节点 s 与节点 t 之间有一条边。

最后一行包含两个正整数，代表起始节点 source 和目标节点 destination。

输出描述

输出一个整数，代表是否存在从节点 source 到节点 destination 的路径。如果存在，输出 1；否则，输出 0。

example:输入示例：
5 4
1 2
1 3
2 4
3 4
1 4
输出：1

DFS方法

可以看成是和前面一样找路径的方法，延伸出DFS和路径规划两种，不同的是这里不是走格子，不用定义dir方向，从src开始，只需要递归邻接矩阵不为0的元素即可，为了防止自己递归自己，邻接矩阵的对角线也设置为0。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
#include <vector>
using namespace std;
class Solution{
public:
    int n;  //n个顶点
    int des;
    Solution(int n,int des):n(n),des(des){}
    bool dfs(vector<vector<int>>& db_Array,vector<bool>& visited,int src){
        if(src==des)  //递归能走到des结点，说明是可达的
            return true;
        visited[src] = true;  //标记
        for(int i=1; i<=n; i++){  //遍历
            if(visited[i]==false&&db_Array[src][i]==1){  //没访问过、且为邻结点
                if(dfs(db_Array,visited,i)==true)  //递归遍历
                    return true;
            }
        }    
        return false; //保证bool类型完整返回，不然提示“指针越界”。
    }  
};


int main(){
    int n,m;
    cin>>n>>m; //n个顶点，m条边
    vector<vector<int>>db_Array(n+1,vector<int>(n+1));
    vector<bool>visited(n+1,false);
    
    int st,end;
    while(m--){
        cin>>st>>end;
        db_Array[st][end] = 1; //可达记1
        db_Array[end][st] = 1;  //无向图对称
    }
    
    int src,des;
    cin>>src>>des;
    
    Solution mySolution(n,des);
    if(mySolution.dfs(db_Array,visited,src)==true)
        cout<<1<<endl;
    else
        cout<<0<<endl;

    return 0;
}

路径规划算法

任何可达路径可以拆分为两个基本问题：i、j是否直接可达，i、j是否可以通过中间点k而可达。因此只需要构造dp数组，根据邻接矩阵即可得到i、j可达结果，再加一层k循环，让通过中间点可达的也连接起来即可。

此时dp矩阵的含义就是：横坐标编号结点如果能到达纵坐标结点（无向图，反过来亦可），则该坐标值为true。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <vector>
using namespace std;
class Solution{
public:
    int n; //顶点
    Solution(int n):n(n){}
    bool get_dpArray(vector<vector<int>>& db_Array,int src,int des){
        vector<vector<bool>>dp(n+1,vector<bool>(n+1,false));
        for(int i=1; i<=n; i++){
            for(int j=1; j<=n; j++){
                if(db_Array[i][j]==1||i==j){  //i、j邻接、自身可达
                    dp[i][j] = true;
                    dp[j][i] = true;
                }
            }
        }
        
        for(int i=1; i<=n; i++){
            for(int k=1; k<=n; k++){
                for(int j=1; j<=n; j++){
                    if(dp[i][k]==true&&dp[k][j]==true&&i!=k&&k!=j){  //通过中间点k可达，i、j也一定可达
                        dp[i][j] = true;
                        dp[j][i] = true;
                    }
                }
            }
        }
        return dp[src][des];  //dp[des][src]
    
    }
};

int main(){
    int n,m;
    cin>>n>>m; //n个顶点，m条边
    vector<vector<int>>db_Array(n+1,vector<int>(n+1));
    
    int st,end;
    while(m--){
        cin>>st>>end;
        db_Array[st][end] = 1; //可达记1
        db_Array[end][st] = 1;  //无向图对称
    }
    
    int src,des;
    cin>>src>>des;
    
    Solution mySolution(n);
    if(mySolution.get_dpArray(db_Array,src,des)==true)
        cout<<1<<endl;
    else
        cout<<0<<endl;

    return 0;
}

并查集算法

图的可达性能看成是否构成连通图，也即通过并查集确定两个点是否在一个集合。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <iostream>
#include <vector>
using namespace std;
class Solution{
public:
    int n; //顶点
    vector<int>unifind;
    Solution(int n):n(n),unifind(n+1){}
    
    void init(){
        for(int i=0; i<=n; ++i){
            unifind[i] = i;
        }
    }
    
    int find(int elem){
        if(elem==unifind[elem])
            return elem;
        return unifind[elem] = find(unifind[elem]); //找父亲、成为父亲
    }
    
    void join(int elem1,int elem2){
        elem1 = find(elem1);
        elem2 = find(elem2);
        if(elem1==elem2)
            return;
        unifind[elem2] = elem1;
    }
    
    bool isSame(int elem1,int elem2){
        elem1 = find(elem1);
        elem2 = find(elem2);
        return elem1==elem2;
    }
    
};

int main(){
    int n,m;
    cin>>n>>m; //n个顶点，m条边
    
    Solution mySolution(n);
    mySolution.init();
    
    int st,end;
    while(m--){
        cin>>st>>end;
        mySolution.join(st,end);  //存在边，将其结点加入并查集
    }
    
    int src,des;
    cin>>src>>des;

    cout<<mySolution.isSame(src,des);
    
    return 0;
}

无向图的最小生成树算法

图去除一些边就成为了生成树，生成树保证了每一点都是可达的（图本身是连通图），节省了冗余路径成本，最小生成树能够模拟和解决不少的实际问题，这里的最小生成树算法都只能解决带权无向图的最小生成树问题。

带全无向图计算最小生成树有prim（普里姆）算法和Kruskal（克鲁斯卡尔）算法，二者的思想基本一致，前者维护点，不断将点加入生成树，适用于边比较多的图（稠密图）；后者维护边，不断加边形成生成树，适用于边比较少的图（稀疏图）。

在世界的某个区域，有一些分散的神秘岛屿，每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路，方便运输。

不同岛屿之间，路途距离不同，国王希望你可以规划建公路的方案，如何可以以最短的总公路距离将 所有岛屿联通起来（注意：这是一个无向图）。

给定一张地图，其中包括了所有的岛屿，以及它们之间的距离。以最小化公路建设长度，确保可以链接到所有岛屿。

输入描述

第一行包含两个整数V 和 E，V代表顶点数，E代表边数 。顶点编号是从1到V。例如：V=2，一个有两个顶点，分别是1和2。

接下来共有 E 行，每行三个整数 v1，v2 和 val，v1 和 v2 为边的起点和终点，val代表边的权值。

输出描述

输出联通所有岛屿的最小路径总距离

example:输入示例 7 11
1 2 1
1 3 1
1 5 2
2 6 1
2 4 2
2 3 2
3 4 1
4 5 1
5 6 2
5 7 1
6 7 1
输出示例:6 示意图

Prim普里姆算法（加点法）

prim算法是贪心算法，要求得最小生成树，首先从某个结点出发（一般为第一个结点），找到邻近结点中边权值最小的加入生成树，然后继续查找其他与这两个生成树结点边权值最小的结点加入生成树，依次类推逐渐构建出生成树就是最小生成树。

使用一个minDst数组记录每次生成树的邻近结点与生成树的权值距离，来决定它是否会在下一次迭代中加入生成树，不和生成树所有邻近的结点都被记为一个极大数。因为记录的始终是和生成树最小距离，而不是和上一个结点的最小距离，因此这是贪心算法，而非DFS。

最小生成树v个顶点一定是v-1条边，v个顶点需要v-1次i循环，每次i循环都会构造一条边，会在minDst数组查找权值最小的，代表它是前几次迭代距离生成树最小距离的结点，将其加入生成树，更新其他点到生成树的距离（因为cur加入，距离会发生改变）。结果minDst数组第2个数开始，所有的minDst值就是最小生成树的权值。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
class Solution{
public:
    int v; //顶点数
    vector<int>minDst; //max val=10000,align with Node number
    vector<bool>inTree; //align with Node number,0 is invalid data
    Solution(int v):v(v),minDst(v+1,INT_MAX-1),inTree(v+1,false){}
    int result=0;
    void get_result(vector<vector<int>>& db_Array){
        for(int i=1; i<=v-1; i++){  //v个顶点，需要循环v-1次构造v-1条边
            int minVal = INT_MAX;  //比minDst初始大
            int cur = 0;  //无效位
            for(int j=1; j<=v; j++){  //与生成树距离最小的结点j，记为cur，第一次cur=1
                if(inTree[j]==false&&minDst[j]<minVal){
                    minVal = minDst[j];
                    cur = j;
                }
            }
            inTree[cur] = true;  //加入生成树
             
            for(int j=1; j<=v; j++){  //更新cur和其他的边的minDst
                if(inTree[j]==false&&db_Array[cur][j]<minDst[j]){
                    minDst[j] = db_Array[cur][j];
                }    
            }
        
        }

        for(int i=2; i<=v; i++){
            result += minDst[i];
        }
    }
};

int main(){
    int v,e;  //v个顶点，e条边
    cin>>v>>e;
    
    //初始时全部权值为无限，用最大val+1代替
    vector<vector<int>>db_Array(v+1,vector<int>(v+1,INT_MAX)); //+1为了和编号对齐
    
    int v1,v2,val; //边起点、终点、权值
    while(e--){
        cin>>v1>>v2>>val;  //替换具体权值代表连接关系
        db_Array[v1][v2] = val;
        db_Array[v2][v1] = val; //无向图对称
    }

    Solution mySolution(v);
    mySolution.get_result(db_Array);
    cout<<mySolution.result<<endl;

    return 0;
}

Kruskal克鲁斯卡尔算法（加边法）

假设图所有点都是孤立的，逐渐选取权值最小的开始加边，此时还有一个重要原则：每次加边都必须使至少两个非连通分量组成一个连通图，例如A——B——C已经连接，尽管A——C边权值是剩下的边最小的，也不应该加，因为没有形成新的连通图，这样就能避免冗余的环，最后成为一个连通图，就是最小生成树。

从carl那学习了定义一个新结构edge用于存储边的信息，维护边就无需邻接矩阵了。假设边的结点都不在并查集，就加入这个边，总体还是清晰的： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

struct edge{
  int st,end,val; //边起点、终点、权值
};
class Solution{
public:
    int v;  //顶点数
    vector<int> unifind; //并查集判断两个点是否一个连通图
    Solution(int v):v(v),unifind(v+1){}  //+1 for align
    //构建并查集：
    void unifind_init(){ 
        for(int i=1; i<=v; i++){
            unifind[i] = i;
        }
    }
    
    int find(int elem){
        if(elem==unifind[elem])
            return elem;
        else
            return unifind[elem] = find(unifind[elem]); //找根，接根
    }
    
    void unifind_join(int elem1,int elem2){
        elem1 = find(elem1);
        elem2 = find(elem2);
        if(elem1 == elem2) //同集合，无需插入
            return;
        unifind[elem2] = elem1;  //不同集合，elem1成为elem2根
    }
    
    bool isSame(int elem1, int elem2){
        elem1 = find(elem1);
        elem2 = find(elem2);
        return elem1 == elem2;
    }
    
    //Kruskal算法：
    int result = 0;
    //静态函数自定义排序：静态函数属于类，而不是示例
    //普通成员函数需要sort提供this指针，而sort没有这个特性
    static bool myCompare(edge e1,edge e2){
        return e1.val < e2.val;  //权值从小到大 
    }
    
    void get_result(vector<edge>& vp){
        sort(vp.begin(),vp.end(),myCompare);  //边权值小的优先被选中
        unifind_init();
        for(edge pos:vp){  
            if(isSame(pos.st,pos.end)==false){ //两个点不在一个并查集/不同连通图
                unifind_join(pos.st,pos.end);  //加入
                result += pos.val; //计算权值和，为最小生成树权值和
            }
        }
    }
};


int main(){
    int v,e; //v个顶点，e条边
    cin>>v>>e;
    
    vector<edge>vp; 
    
    int st,end,val; //边起点、终点、权值
    while(e--){
        cin>>st>>end>>val;
        vp.push_back({st,end,val});  //记录边信息
    }
    
    Solution mySolution(v);
    mySolution.get_result(vp);
    cout<<mySolution.result<<endl;
    
    return 0;
}

拓展：类内仿函数、结构体重载括号、lambda匿名表达式的一些排序写法： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//类内仿函数
bool operator()(edge e1,edge e2)const{
    return e1.val < e2.val;  //权值从小到大 
}
//调用
sort(vp.begin(),vp.end(),*this);  //this指向的是本类实例指针，解引用的重载括号仿函数作为比较器

//类外结构体重载括号：
struct mycompare{
    bool operator()(edge e1,edge e2)const{
        return e1.val < e2.val;  //权值从小到大 
    }
};
//调用
sort(vp.begin(),vp.end(),myCompare());

//匿名函数
sort(vp.begin(), vp.end(), [](const Edge& e1, const Edge& e2) {
            return e1.val < e2.val;
});

拓扑排序：软件依赖/大学排课问题

某个大型软件项目的构建系统拥有 N 个文件，文件编号从 0 到 N - 1，在这些文件中，某些文件依赖于其他文件的内容，这意味着如果文件 A 依赖于文件 B，则必须在处理文件 A 之前处理文件 B （0 <= A, B <= N - 1）。请编写一个算法，用于确定文件处理的顺序。

输入描述：

第一行输入两个正整数 N, M。表示 N 个文件之间拥有 M 条依赖关系。

后续 M 行，每行两个正整数 S 和 T，表示 T 文件依赖于 S 文件。

输出描述：

输出共一行，如果能处理成功，则输出文件顺序，用空格隔开。

如果不能成功处理（相互依赖），则输出 -1。

example:输入
5 4
0 1
0 2
1 3
2 4
输出
0 1 2 3 4

BFS方法：寻找没有依赖的（入度为0）结点首先加入队列，查看与该节点的其他结点，删除与本结点的依赖后是否入度为0，如果是则加入队列处理，不是说明该结点仍依赖其他结点，应该靠后排序；如是处理后，如果存在为入队的情况，说明依赖序列存在循环依赖的环状情况，这个时候只能返回-1； 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <iostream>
#include <vector>
#include <unordered_map>
#include <queue>
using namespace std;

class Solution{
public:  
    int n;
    Solution(int n):n(n){};
    vector<int>result;
    void bfs(vector<int>&indegree,unordered_map<int,vector<int>>&umap){
        queue<int>que;
        for(int i=0;i<n;i++){
            if(indegree[i]==0)
                que.push(i);  //入度为0起点
        }
        while(!que.empty()){  
            int tempid = que.front(); //本文件
            que.pop();
            result.push_back(tempid);
            if(umap[tempid].size()){ //存在其他文件依赖本文件
                for(int i=0;i<umap[tempid].size();i++){
                    indegree[umap[tempid][i]]--; 
                    if(indegree[umap[tempid][i]]==0)
                        que.push(umap[tempid][i]);
                }
            }
        }
    }
};

int main(){
    int n,m; //n个文件m个依赖关系
    cin>>n>>m;
    vector<int>indegree(n); //n个文件的入度
    
    int s,t;
    unordered_map<int,vector<int>> umap; //本文件、与本文件有映射的文件
    while(m--){
        cin>>s>>t;
        indegree[t]++; //t文件入度++，代表依赖于其他文件
        umap[s].push_back(t); //哈希表的一对多设计
    }
    
    Solution mySolution(n);
    mySolution.bfs(indegree,umap);
    
    if(mySolution.result.size()!=n){  //说明没有全部入队（存在循环情况）
        cout<< -1<<endl;
        return 0;
    }
        
    for(int i=0;i<n-1;i++)  //打印结果
        cout<<mySolution.result[i]<<'\t';
    cout<<mySolution.result[n-1]<<endl;

    return 0;
}

带非负权的有向图两点最短路径

小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。

小明的起点是第一个车站，终点是最后一个车站。然而，途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素（如天气变化）等不同，这些因素都会影响每条路径的通行时间。

小明希望能选择一条花费时间最少的路线，以确保他能够尽快到达目的地。

输入描述 第一行包含两个正整数，第一个正整数 N 表示一共有 N 个公共汽车站，第二个正整数 M 表示有 M 条公路。

接下来为 M 行，每行包括三个整数，S、E 和 V，代表了从 S 车站可以单向直达 E 车站，并且需要花费 V 单位的时间。

输出描述 输出一个整数，代表小明从起点到终点所花费的最小时间。

example:输入示例:
7 9
1 2 1
1 3 4
2 3 2
2 4 5
3 4 2
4 5 3
2 6 4
5 7 4
6 7 9
输出示例:12
示意图

暴力DFS+回溯

几乎没有参考价值，递归的计算复杂度太高。。。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <vector>
#include <climits>

using namespace std;


class Solution{
public:
    int result= INT_MAX;
    int temp_sum=0;
    int n; //顶点数
    bool flag = false; //是否可达
    Solution(int n):n(n){} 
    
    void dfs(vector<vector<int>>& db_Array,int src,int des){
        if(src==des&&temp_sum < result){
            result = temp_sum;
            flag = true;
            return;
        }
        
        for(int i=1; i<=n; i++){
            if(db_Array[src][i]!=0){
                temp_sum += db_Array[src][i];
                dfs(db_Array,i,des);
                temp_sum -= db_Array[src][i];
            }
        }
    }
};

int main(){
    int n,m; //n个顶点，m条边
    cin >>n>>m;
    
    vector<vector<int>>db_Array(n+1,vector<int>(n+1));
    
    int st,end,val;  //有向边起点、终点、权值
    while(m--){
        cin>>st>>end>>val;
        db_Array[st][end] = val;
    }
    
    Solution mySolution(n);
    mySolution.dfs(db_Array,1,n);
    if(mySolution.flag == false)
        cout<<-1<<endl;
    else
        cout<<mySolution.result<<endl;
    
    return 0;
}

Dijkstra迪杰斯特拉算法

尽量维持prim算法风格，以免过多差别发生混淆，主要不同在于dijkstra需要将minDst起点坐标元素置0，此题默认总是从顶点1出发；其次，最小生成树的目标是找到权值最小的边，因此每次更新的是非生成树结点到生成树的距离,minDst[j] = db_Array[cur][j]，这里要求的是源点和目标点的距离，minDst本身是已遍历路径某个点到原点的最小距离，加入新点只需要加上其边值再和原值比较即可，即minDst[j] = minDst[cur] + db_Array[cur][j]

还有很容易忘记的是记得将邻接矩阵非连接权值、minDst初始值设置成极大值。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <iostream>
#include <vector>
#include <climits>

using namespace std;

class Solution{
public:
    //Dijkstra算法
    int n; //顶点数
    //prim算法、Dijkstra维护数组
    vector<int>minDst; 
    vector<bool>visited;
    //vector<int>path;  //路径记录
    //如果需要路径：构造函数加上path(n+1)
    Solution(int n):n(n),minDst(n+1,INT_MAX-1),visited(n+1,false){} //+1 for align
    
    void get_result(vector<vector<int>>& db_Array,int des){
        minDst[1] = 0;  //起点置0，如果不是从1开始就修改
        for(int i=1; i<=n; i++){  //区别于prim：循环顶点
            int cur = 0;
            int minVal = INT_MAX;   //维持prim风格，总是能被minDst替代
            for(int j=1; j<=n; j++){
                if(visited[j]==false&&minDst[j] < minVal){
                    minVal = minDst[j];
                    cur = j;
                }
            }
                 
            visited[cur] = true;
            
            for(int j=1; j<=n; j++){
                //db_Array[cur][j]限定，防止加法越界（成为极大的负数），minDst[cur]判不判断均可
                //因为起点手动置0，更新总会快于加法
                if(visited[j]==false&&db_Array[cur][j]!=INT_MAX&&minDst[cur] + db_Array[cur][j]< minDst[j]){
                    minDst[j] = minDst[cur] + db_Array[cur][j];
                    //path[j] = cur;  //如果需要记录路径
                }
                    
            }
        }    
        
        if(minDst[des]== INT_MAX-1)
            cout<<-1<<endl;
        else 
            cout<<minDst[des]<<endl;
        
        // //打印路径
        // for(int i=2; i<=n; i++){
        //         cout<<path[i]<<"->"<<i<<" ";
        // }
    }
};

int main(){
    int n,m; //n个顶点，m条边
    cin >>n>>m;
    
    vector<vector<int>>db_Array(n+1,vector<int>(n+1,INT_MAX));
    
    int st,end,val;  //有向边起点、终点、权值
    while(m--){
        cin>>st>>end>>val;
        db_Array[st][end] = val;
    }
    
    Solution mySolution(n);
    mySolution.get_result(db_Array,n);

    return 0;
}

dijkstra算法为什么需要非负权值

模拟得到的minDst数组如下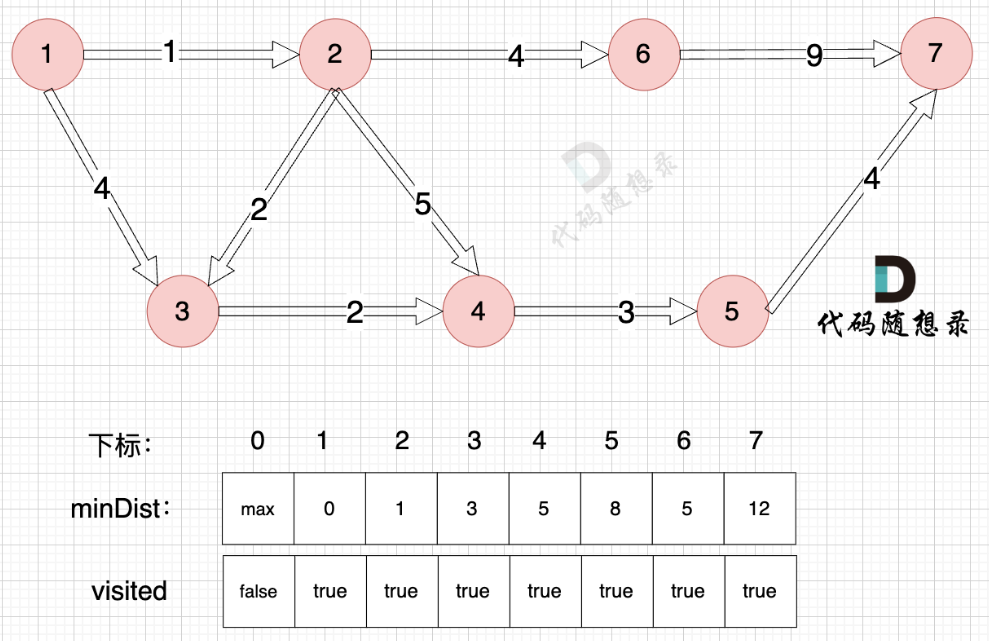： minDst数组 算法流程如下：从起点（顶点1）开始置0，然后遍历其邻边，1到2、1到3权值替代起始权值，2、3均标记为访问，然后会进一步更新2、4和2、6，3、4的权值，最后minDst每个值都对应本点到达源点的最小权值。

因此这里有个问题，假如1——3权值为1，2——3权值为-2，那么1——3的最佳路径应该是1——2——3，但是在第一步时，1——3权值已经被确定，代码不会重新审视2——3的权值（因为visited[2]==true&&visited[3]==true），1——3的权值不会再被更新，因此Dijkstra算法不能被用于计算负权的最短路径。

dijstra获取路径

在代码中使用path用于记录前驱编号，例如path[2]=1，就代表1下一个会走到2，即1是2的前驱。（打印会顺便打印不是最终路径，但是连通的路径（如2->6）,根据题目进一步筛选即可）。

带负权的有向图两点最短路径

带负权的权值代表路径不仅没有损耗，还会带来收益，这种情况下追求最低成本/最大收益，也是一种最短路径问题，但是图要确保一个前提：即不能构成负权回路，负权回路能够无限刷钱/增加收益，确实能增大收益，但是干扰正常计算。这个前提既可以是题目确保的，也可以通过贝尔曼-福特算法判断。

某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。

网络中的道路都有各自的运输成本和政府补贴，道路的权值计算方式为：运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用；权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。

请找出从城市 1 到城市 n 的所有可能路径中，综合政府补贴后的最低运输成本。如果最低运输成本是一个负数，它表示在遵循最优路径的情况下，运输过程中反而能够实现盈利。

城市 1 到城市 n 之间可能会出现没有路径的情况，同时保证道路网络中不存在任何负权回路。

输入描述

第一行包含两个正整数，第一个正整数 n 表示该国一共有 n 个城市，第二个整数 m 表示这些城市中共有 m 条道路。

接下来为 m 行，每行包括三个整数，s、t 和 v，表示 s 号城市运输货物到达 t 号城市，道路权值为 v （单向图）。

输出描述

如果能够从城市 1 到连通到城市 n， 请输出一个整数，表示运输成本。如果该整数是负数，则表示实现了盈利。如果从城市 1 没有路径可达城市 n，请输出 "unconnected"。

example:输入示例 6 7
5 6 -2 1 2 1
5 3 1
2 5 2
2 4 -3 4 6 4
1 3 5
输出示例:1 示意图

Bellman-ford贝尔曼-福特算法

术语：relax the edge松弛：我理解是更新权值，Dijkstra算法中不会回头审视和更新那些走过的路径权值，而带负权的算法加入了新顶点，同时加入了新的边，这条边的负值补偿可能能弥补以前走过的高权值路径，使得净消耗值更低，因此回头比较、更新权值这样的“松弛”操作很有必要。

Bellman_ford松弛一次（更新一次minDst）的效果是：能得到从起点走一次的情况下到达某个点的最短路径（不可达的记为max）。松弛两次的效果是：从起点走两次的情况下，到某个点的最短路径；因此一个n个连通图的最远顶点距离最多经过n-1条边，n-1次松弛后，任意两点的最短路径是可知的。

Bellman-ford算法和Kruskal算法类似，后者是维护边找到最小的生成树，贝尔曼-福特同样也是维护边，它会遍历每条边，将起点minDst置0，每次拿到边的终点，都会比较到其起点位置的路径是否比现有路径权值更小，如果是则需要进行松弛操作。

这里还实现了一个demo，在Dijkstra或者Bellman-ford算法不仅需要计算最短路径权值，还需要知道规划路径元素时实现记录输出，思路是记录其前驱，类似并查集的方法进行搜索即可。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <iostream>
#include<vector>
#include <climits>
//#include <algorithm>  //for std::reverse
using namespace std;
struct edge{
  int st,end,val; //有向边起点、终点、权值  
};

class Solution{
public:
    int n;  //顶点数
    vector<int>minDst;
    //vector<int>path;  //if need path
    //path(n+1,-1)
    Solution(int n):n(n),minDst(n+1,INT_MAX){}
    void get_result(vector<edge>& vp,int src,int des){
        minDst[src] = 0;
        for(int i=1; i<=n-1; i++){ //松弛n-1次
            for(edge pos:vp){
                if(minDst[pos.st]!=INT_MAX && minDst[pos.st] + pos.val < minDst[pos.end]){
                    minDst[pos.end] = minDst[pos.st] + pos.val; //
                    //path[pos.end] = pos.st; //if need path，记录新路径前驱
                }
            }
        }
        
        if(minDst[des]==INT_MAX)
            cout<<"unconnected"<<endl;
        else
            cout<<minDst[des]<<endl;
        
        //如果题目需要获取最短路径，以下，如输出1256
        /*
        vector<int>path_output;  //从path中筛选最终路径
        while(path[n]!=-1){   //从终点往前找，就像并查集一样，直到找到起点
            path_output.push_back(n);  
            n = path[n];
        }
        path_output.push_back(1); //压入起点
        reverse(path_output.begin(),path_output.end()); //颠倒，从起点到终点路径
        for(auto i:path_output)
            cout<<i<<" ";
        */
    }
    
};


int main(){
    int n,m;  //n个顶点、m条边
    cin>>n>>m;
    
    vector<edge>vp;

    int st,end,val;
    while(m--){
        cin>>st>>end>>val;
        vp.push_back({st,end,val});
    }
    
    Solution mySolution(n);
    mySolution.get_result(vp,1,n);
    
    return 0;
}

Bellman-ford算法判断负权回路

负权回路的特性是不断刷钱/增加收益，导致贝尔曼-福特算法无法获得最短路径，n个顶点的图正常算法松弛n-1次能得到任意两点的最短路径，带负权回路的图minDst超过n-1次时，路径仍然会不断更新，因此只需要判断松弛n次的minDst数组和松弛n-1次数组是否一致，即可判断图是否出现负权回路。

某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。

网络中的道路都有各自的运输成本和政府补贴，道路的权值计算方式为：运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用；权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。

然而，在评估从城市 1 到城市 n 的所有可能路径中综合政府补贴后的最低运输成本时，存在一种情况：图中可能出现负权回路。负权回路是指一系列道路的总权值为负，这样的回路使得通过反复经过回路中的道路，理论上可以无限地减少总成本或无限地增加总收益。为了避免货物运输商采用负权回路这种情况无限的赚取政府补贴，算法还需检测这种特殊情况。

请找出从城市 1 到城市 n 的所有可能路径中，综合政府补贴后的最低运输成本。同时能够检测并适当处理负权回路的存在。

城市 1 到城市 n 之间可能会出现没有路径的情况

输入描述

第一行包含两个正整数，第一个正整数 n 表示该国一共有 n 个城市，第二个整数 m 表示这些城市中共有 m 条道路。

接下来为 m 行，每行包括三个整数，s、t 和 v，表示 s 号城市运输货物到达 t 号城市，道路权值为 v。

输出描述

如果没有发现负权回路，则输出一个整数，表示从城市 1 到城市 n 的最低运输成本（包括政府补贴）。如果该整数是负数，则表示实现了盈利。如果发现了负权回路的存在，则输出 "circle"。如果从城市 1 无法到达城市 n，则输出 "unconnected"。

example:输入示例
4 4
1 2 -1 2 3 1
3 1 -1 3 4 1
输出示例:circle

在Bellman-ford算法基础上增加n和n-1数组的比较逻辑即可： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <vector>
#include <climits>

using namespace std;
struct edge{
    
  int st,end,val; //边起点、终点、权值  
    
};

class Solution{
public:
    int n; //顶点数
    vector<int>minDst;
    Solution(int n):n(n),minDst(n+1,INT_MAX){}
    void get_result(vector<edge>& vp,int src,int des){ 
        minDst[src] = 0;
        vector<int>minDst_nm1;
        for(int i=1; i<=n; i++){ //尝试松弛n次
            
            for(edge pos:vp){
                //防止加法越界，更新和前面结点连接的权值——松弛
                if(minDst[pos.st]!=INT_MAX&&minDst[pos.st] + pos.val < minDst[pos.end])
                    minDst[pos.end] = minDst[pos.st] + pos.val;
            }
            if(i==n-1)  //记录n-1次松弛的minDst结果
                minDst_nm1 = minDst;
        }
        
        if(minDst_nm1!=minDst)  //不等，说明存在刷钱行为，即有负权回路
            cout<<"circle"<<endl;
        else if(minDst_nm1[des]==INT_MAX) //不可达
            cout<<"unconnected"<<endl;
        else
            cout<<minDst_nm1[des]<<endl;
    }

};

int main(){
    int n,m;  //n个顶点，m条边
    cin>>n>>m;
    
    vector<edge>vp;
    int st,end,val;  //边起点、终点、权值
    while(m--){
        cin>>st>>end>>val;
        vp.push_back({st,end,val});
    }
    
    Solution mySolution(n);
    mySolution.get_result(vp,1,n);

    return 0;
}

Bellman-ford解决单源局部最短路径

Bellman-ford还有一个重要的应用，是计算局部的最短路径，也即限定只能走k步。这样一个应用是在路由中，我们知道路由数据报的跳数由TTL规定，且路由可能只有分散信息（局部信息）。原理上其实早就介绍了，因为贝尔曼-福特算法每松驰k次，就对应只走k步的情况下的可达最短路径，但是考虑负权回路的话，就要增加额外的逻辑。

某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。

网络中的道路都有各自的运输成本和政府补贴，道路的权值计算方式为：运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用；权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。

请计算在最多经过 k 个城市的条件下，从城市 src 到城市 dst 的最低运输成本。

输入描述

第一行包含两个正整数，第一个正整数 n 表示该国一共有 n 个城市，第二个整数 m 表示这些城市中共有 m 条道路。

接下来为 m 行，每行包括三个整数，s、t 和 v，表示 s 号城市运输货物到达 t 号城市，道路权值为 v。

最后一行包含三个正整数，src、dst、和 k，src 和 dst 为城市编号，从 src 到 dst 经过的城市数量限制。

输出描述

输出一个整数，表示从城市 src 到城市 dst 的最低运输成本，如果无法在给定经过城市数量限制下找到从 src 到 dst 的路径，则输出 "unreachable"，表示不存在符合条件的运输方案。

example:输入示例
6 7
1 2 1
2 4 -3 2 5 2
1 3 5
3 5 1
4 6 4
5 6 -
2 6 1
输出示例: 0

首先要注意，测试用例的经过k个城市，是不计算起点和终点的，因此经过k个城市，实际上能走k+1步而不是k-1步；

Bellman-ford算法负权回路具体分析

在前文记录了判断负权回路的方法是判断minDst数组是否不断更新（例如n次和n-1次时），现在在负权回路的背景下，讨论如何输出正确的权值。

这里为了应对负权回路问题，我们需要记录上一次松弛的数据，作为更新权值的依据，理由如下，还是以卡哥做的图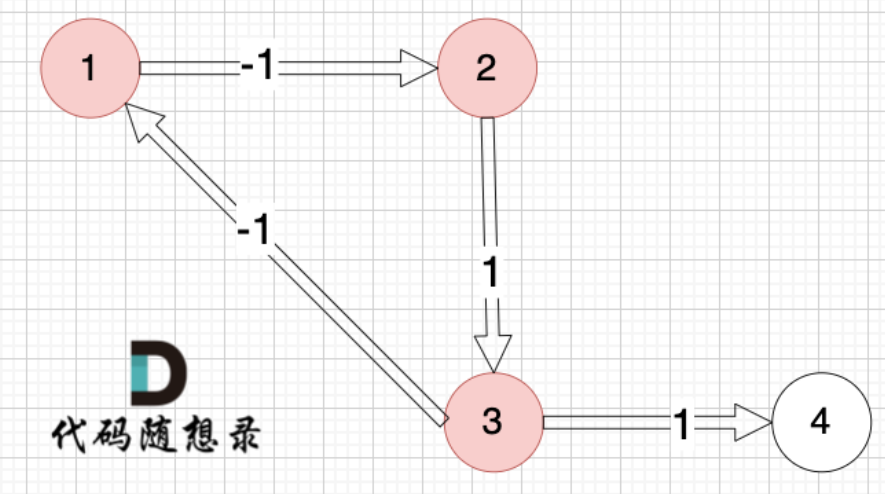： 负权回路的值 先考虑非负权回路情况，假设图中3->1权值改成1，破坏负权回路，那么松弛第一次的数组是：minDst[1]=0,1指向2，2更新为-1，2指向3，3更新为0，3指向1，但1>0,1不更新，3指向4，4更新为1，即minDst[1-4]={0,-1,0,1}；4个顶点最多松弛3次就能得到最短路径，但是这图比较特别（不是完全图），现在已经得到最佳路径，也即再松弛，minDst也不会发生改变。

现在再考虑图中的情况，3->1为-1，构成了一条负权回路：minDst[1]=0,1指向2，2更新为-1，2指向3，3更新为0；和上面唯一不同的是，再遍历3—>1边时，权值为-1，minDst[3]-1<min[1]，因此min[1]会被更新成-1。最后min[4]仍然为1，即minDst[1-4]={-1,-1,0,1}；

说明1被同一次松弛更新了两次（carl原文此处说3被更新两次应该有误，或者理解成因为3而导致1被更新），于是进行第二次松弛，minDst[1]为-1，1指向2，2被更新成-2，2指向3，3被更新成-1，3指向1，1被更新成-2，最后4被更新成0，即minDst[1-4]={-2,-2,-1,0}；此后每次松弛的结果就是前一次数组所有元素-1；

可见每次松弛，刷钱的操作就是不断使得minDst得到负权回路的增益，这是一种链式反应，此时已经不能得到正确的路径了。

因此要解决这个问题，就是从链式反应的起点开始杜绝，这题是因为第一次松弛遍历3—>1边时，结点1被二次松弛更新minDst[1]=-1，对于其他图，二次松弛更新可能发生在其他坐标；因此在遍历边前，应该提前记录初始化的minDst，这样更新权值时仍然依靠的是minDst_last[1] = 0,就不会发生上述问题了。

最终代码如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <vector>
#include <climits>

using namespace std;
struct edge{
  
  int st,end,val;  //边起点、终点、权值；  
    
};
class Solution{
public:
    int n; //顶点数
    vector<int>minDst;
    Solution(int n):n(n),minDst(n+1,INT_MAX){}
    void get_result(vector<edge>& vp,int src,int des,int k){
        minDst[src] = 0;
        vector<int>minDst_last(n+1,INT_MAX);
        for(int i=1; i<=k+1; i++){  //走k+1步，最多k个城市
            minDst_last = minDst;
            for(edge pos:vp){
                if(minDst_last[pos.st]!=INT_MAX&&minDst_last[pos.st] + pos.val < minDst[pos.end])
                    minDst[pos.end] = minDst_last[pos.st] + pos.val;
            }
        }
        
        if(minDst[des]==INT_MAX)
            cout<<"unreachable"<<endl;
        else
            cout<<minDst[des]<<endl;
 
    }
   
};

int main(){
    int n,m;  //n个顶点、m条边
    cin>>n>>m;
    
    vector<edge>vp;
    int st,end,val;
    while(m--){
        cin>>st>>end>>val;
        vp.push_back({st,end,val});
    }
    
    int src,des,k; //起点、终点、最多经过k个城市（走k-1步）
    cin>>src>>des>>k;
    
    Solution mySolution(n);
    mySolution.get_result(vp,src,des,k);
    
    return 0;
}

多源任意权值任意向图最短路径：Floyd算法

多源最短路径是不单独指定某个起点的情况下讨论的最短路径算法，应该指出的是，多源路径问题能够降维成多个单源最短路径问题，只要将迪杰斯特拉算法、贝尔曼-福特算法封装成能够接收起点、终点参数的函数即可，都是通过将minDst[src]=0开始推理，注意如果是无向图问题还要将原来的有向图逻辑改成无向图逻辑，但是毕竟多次推理，时间复杂度也更高，专门针对多源路径问题的有这个弗洛伊德算法，通过动态规划能得到任意两点的最短路径。

在《寻找存在的路径》那一节中，了解了图中某个点到某个点是否可达，实际上就是两个基本问题：要么直接可达，要么通过中间点可达，也即最高是三维问题。因此权值更新时，两个结点最小权值要么就是来自直接可达的结点(邻接矩阵已经算好)，要么来自通过中间点可达的结点，寻找最短路径，实际上是找不同的中间点，通过遍历暴力解决就是了。

小明喜欢去公园散步，公园内布置了许多的景点，相互之间通过小路连接，小明希望在观看景点的同时，能够节省体力，走最短的路径。

给定一个公园景点图，图中有 N 个景点（编号为 1 到 N），以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。

小明有 Q 个观景计划，每个计划都有一个起点 start 和一个终点 end，表示他想从景点 start 前往景点 end。由于小明希望节省体力，他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。

输入描述

第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。

接下来的 M 行，每行包含三个整数 u, v, w，表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。

接下里的一行包含一个整数 Q，表示观景计划的数量。

接下来的 Q 行，每行包含两个整数 start, end，表示一个观景计划的起点和终点。

输出描述

对于每个观景计划，输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径，则输出 -1。

example:输入示例
7 3
2 3 4
3 6 6
4 7 8
2
2 3
3 4
输出示例
4
-1

发现使用INT_MAX和使用一个极大值还是有点区别，要加入大小逻辑判断，而且要更新无向图对角线对称的元素，才能正确通过测试。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
class Solution{
public:
    int n; //顶点数
    Solution(int n):n(n){}
    void get_result(vector<vector<int>>& db_Array, int src, int des){
        for(int i=1; i<=n; i++){
            for(int k=1; k<=n; k++){
                for(int j=1; j<=n; j++){
                    if(db_Array[i][k]!=INT_MAX&&db_Array[k][j]!=INT_MAX){  //防止加法越界
                        //Floyd核心：比较邻接矩阵原值和经过中间点的权值
                        db_Array[i][j] = min(db_Array[i][j],db_Array[i][k]+db_Array[k][j]);
                        db_Array[j][i] = db_Array[i][j];  //无向图及时更新
                    }
                }
            }
        }
        //输出答案
        if(db_Array[src][des]==INT_MAX)
            cout<<-1<<endl;
        else
            cout<<db_Array[src][des]<<endl;
    }
};


int main(){
    int n,m; //n个顶点、m条边
    cin>>n>>m;
    
    vector<vector<int>>db_Array(n+1,vector<int>(n+1,INT_MAX));
    int st,end,val; //边起点、终点、权值
    while(m--){
        cin>>st>>end>>val;
        db_Array[st][end] = val;
        db_Array[end][st] = val; //无向图
    }
    
    int num; //计划数
    cin>>num;
    
    int src,des;
    Solution mySolution(n);
    while(num--){
        cin>>src>>des;
        mySolution.get_result(db_Array,src,des);
    }
    
    return 0;
}