数据结构与算法(三):查找与排序算法
此前的两篇文章介绍了线性表、树、图的基本思想以及相关算法,不难发现有若干算法是需要在有序的前提下实现的,查找和排序在数据结构中常常被当成预处理使用,而反过来,有的数据结构可以载入杂乱的数据供给查找和排序,故二者是相辅相成,相互依赖的,这就是为什么会在数据结构的末章总会提到查找和排序算法的原因,本文记录了相关常用的算法,旧金山大学网站中给出了相关算法的可视化交换页面,非常方便理解和算法验证。
查找
相关术语
查找:在数据集合中寻找某种符合条件数据元素的过程;
查找表:用于查找操作的数据集合,通常用于统称一种数据结构,不是什么新的数据结构。
关键字:可以唯一区别数据对象的数据元素,关键字查找结果必须是唯一的。
静态查找表:只需要对元素进行查找,性能只考虑查找速度即可。
动态查找表:需要对查找表进行元素查找、插入、删除等,性能除了关注查找速度,还要考虑插入删除的复杂度。
查找算法的评价指标
平均查找长度(Average Search Length,ASL):表示查找过程中进行关键字比较次数的平均值,通常对同一个算法要同时考虑查找成功的ASL和查找失败的ASL。
时间复杂度、空间复杂度
1. 顺序查找
1 | typedef int data_t; |
查找成功的ASL是(1+2+3+...+n)/n=(n+1)/2;
查找失败的ASL是n+1;
总体复杂度都是O(n);
优化方法:
哨兵顺序查找:将需要查找的元素放在第一个数据,从数据最后一位往前查找比较,如果返回到0则查找失败;这种方法的好处是无需每一步都判定数组是否越界,但复杂度上是基本一致的。
有序表查找:当查找的数据结构是有序的,那么可以查找到某个大于或者小于目标元素的下标时就停止查找,节省了部分步骤。
带概率元素查找:将查找频率大的元素放在表前,可以优化性能。
2. 折半查找(二分查找)
只适用于有序的顺序表查找。基本思想是比较中间元素和目标元素大小,如果中间元素小于目标元素,那么中间元素之前的就不用看了,begin更新为mid+1,如果大于,那么后面元素就不用看了,end更新为mid-1,这个过程必须严格控制begin<end,否则位置相反导致程序会出错。
1
2
3
4
5
6
7
8
9
10
11
12typedef int data_t;
int Search_half(vector<data_t> &sqlist,data_t Elem){
int begin=0;
int end=sqlist.size()-1;
int mid=(begin+end)/2;
while(sqlist[mid]!=Elem&&begin<end){ //保证begin<end,且中间元素不为Elem才更新
sqlist[mid]<Elem?begin=mid+1:end=mid-1;
mid=(begin+end)/2;
}
return sqlist[mid]==Elem?mid:-1; //中间元素就是Elem,则返回下标
}
时间复杂度:O(logn)
分析:每次折半查找都只是比较中间结点和目标元素的大小,实际上这是构造二叉排序树的过程,称为折半查找树。左子树必然是比根结点小的元素,右子树是比根结点大的元素,由于更新逻辑是mid=(begin+end)/2,mid是向下取整的,因此奇数、偶数情况下,右子树元素比左子树元素多1或者相等,也即这也是一棵平衡二叉树。对于不同个数的数据集合,只有最下层的元素可以不为满的,也即它类似一棵完全二叉树。
综上所述,完全二叉树结点数为n时,树高为
3. 分块查找
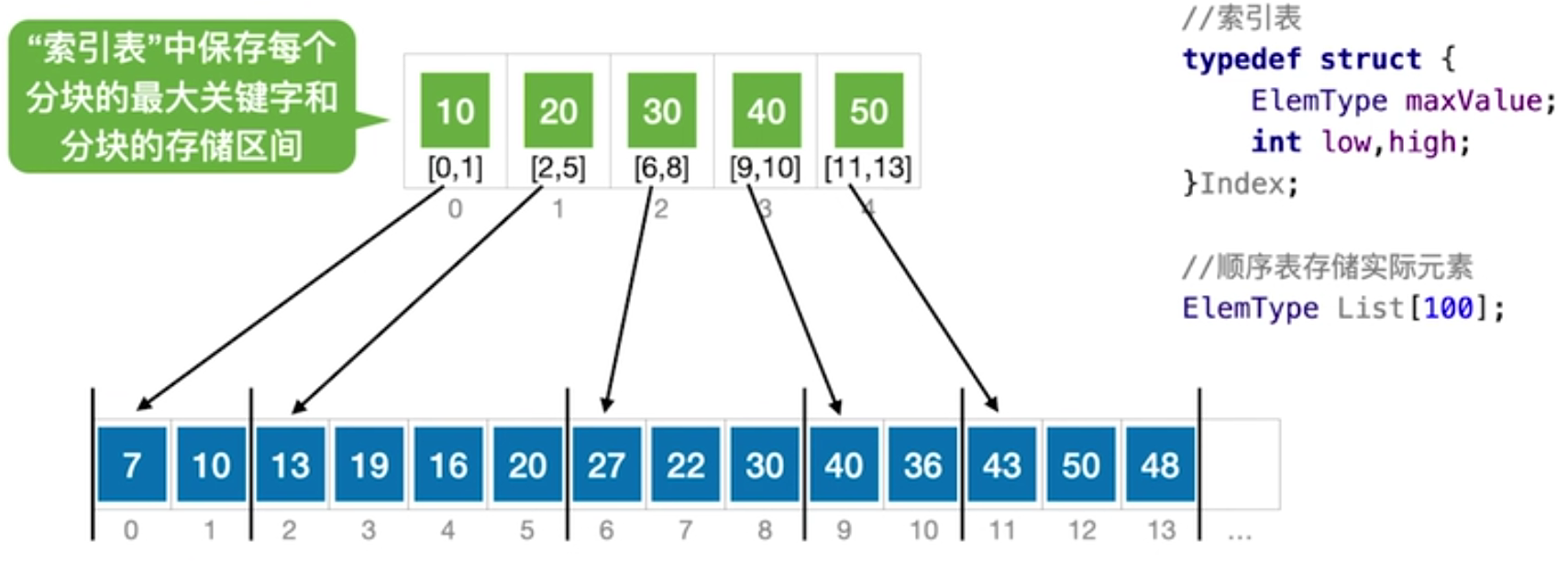 将无序的顺序表划划分为块(划分规则是自定义的),图中按10、20、30、40、50作为最大关键字划分,索引表存储了每个分块的最大关键字,以及分块的最小下标和最大下标。需要查找某个元素时,在分块中首先查找最大的关键字,这又可以分成顺序查找和折半查找的方式,顺序查找时,按顺序遍历分块,直到找到第一个大于目标元素的关键字分块,进入分块执行顺序查找;折半查找时(要求分块关键字是有序的),假设开始时low指向10,high指向50,mid=30,如果查找目标就是30,那么直接进入30分块进行查找;如果目标是27,尽管它在30关键字分块中,但还是先执行折半查找(因为不确定是否有27、28、29的关键字),直到最后的情况是high>low,那么结果就在low指向的30分块中,进入顺序查找27。
将无序的顺序表划划分为块(划分规则是自定义的),图中按10、20、30、40、50作为最大关键字划分,索引表存储了每个分块的最大关键字,以及分块的最小下标和最大下标。需要查找某个元素时,在分块中首先查找最大的关键字,这又可以分成顺序查找和折半查找的方式,顺序查找时,按顺序遍历分块,直到找到第一个大于目标元素的关键字分块,进入分块执行顺序查找;折半查找时(要求分块关键字是有序的),假设开始时low指向10,high指向50,mid=30,如果查找目标就是30,那么直接进入30分块进行查找;如果目标是27,尽管它在30关键字分块中,但还是先执行折半查找(因为不确定是否有27、28、29的关键字),直到最后的情况是high>low,那么结果就在low指向的30分块中,进入顺序查找27。
查找性能:分块查找的性能是介于二分查找和顺序操作直接的一种查找方法,因为块的划分规则不同,性能也有所差异,尤其引入了二分查找的分块查找计算比较复杂。但有一种情况是肯定的:当采取平均分块时,划分的分块数目为根号元素数时,查找性能是最好的。
4. 哈希表(散列表)
哈希表(Hash Table)是一种用于提高查找效率的结构。在查找操作中,如果对顺序表进行逐一查找,那么带来的时间复杂度是O(n)。而哈希表往往能带来常数级的时间复杂度,也即O(1)。哈希表的基本原理是,存储数据时数据的位置是由特定的映射关系决定的,这个映射关系被称为哈希函数(散列函数)。例如需要存储1,2,3,4,5,6....,定义映射函数为n%3,那么1存到下标1、2存到下标2位置、3存到下标0位置...当然问题也是存在的,哈希函数不能把全部元素映射到唯一的位置,例如1、4都会被放到下标1的位置,这种现象称为冲突,引起冲突的两个对象称为同义词。
解决冲突的常用方法是拉链法:下标不直接存储元素,而是指向一个链表,链表中依次存放元素。
性能分析
这种方法查找复杂度仍然是O(1),查找成功的平均查找长度是链表当前层数*元素个数的求和除以元素总个数,查找失败的平均查找长度是元素总个数(记录数)除以哈希表的表长(存放指针的空间),这个也被定义为装填因子(一般为0.7~0、8较为理想,保存部分余量)。
可以看见这种方法的查找效率是依赖于冲突的发生概率的(决定了链表的长度,链表越深查找成功的平均查找长度越大),而冲突发生概率又是依赖于哈希函数的设计,例如上面的例子对应存储1,2,3,4,5,6...带来的冲突比较严重,不是科学的设计方法。
常见的哈希函数设计方法
除留余数法:H(key)=key%p,p的取值原则是假设哈希表长为m,p取不大于m,但最接近m的质数。 使用质数取模对随机的数组更加友好,不容易发生元素集中在某个元素的情况。
直接定址法:H(key)=key或者a*key+b;
这种方法是简单线性的处理方法,比较适用于连续数据比较多的数据。不连续则容易造成浪费。数字分析法:如果存储的数据中有部分数据比较均匀分布,这部分数据可以直接用于充当散列地址。例如手机号后四位为0000的放在0,0001的放在1......
平方取中法:目的还是使数据比较均匀地存储。例如遇到身份证、电话等长数据,可以将其平方后取其结果中间几位作为散列地址。
链地址哈希表实现
以下定义了哈希表的数据结构,这里使用了常用的链式哈希表,最大表长定义为14,这不意味着存放元素的个数最大是14,因为正如上述所说哈希表不直接存放数据,只是指向数据的链表;哈希表的表长只是影响元素查找的效率,以及哈希函数的选取。其次,哈希表常常用于描述一种“键值对”的概念,这和python中的字典键值概念是一致的。哈希表中,键(Key)指的是能唯一找到元素的标识,在这个例子中我们使用了一个数组来定义这些值,原则上哈希表是不允许存在重复的键的(重复也背离了键的定义)。值(Value)指的是元素自己存放的信息,查找并不依靠值,因此值是可重复的,本例中没有设计值的内容,而是用于记录索引信息,但不可认为索引信息就是值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23//hash.h
extern int mold; //取模数,全局变量;
typedef int data_t;
typedef struct node{ //链式结构
data_t key; //键,用于查找元素,可以是不可重复的数据,也可以是无意义的数字
data_t value;//值,存储取模后的位置结果,也可以用于存放元素信息
struct node* next; //指向下一个元素
}listnode,*linklist;
typedef struct{
listnode data[MAXSIZE];//哈希表,表长为14
}hash;
hash *hash_create(); //创建空哈希表
int hash_insert(hash *h,data_t key);//插入元素
linklist hash_search(hash *h,data_t key);//搜索元素key
1 | //hash.c |
1 | //main.c for test |
排序
按照递增或者递减元素的方式进行排序输出(本文使用递增输出逻辑)
排序算法评价指标
稳定性:需要排序的关键字中有若干个重复的元素,初始相对位置在排序后也不应该改变,尽管他们是相同的,具有这样特性的排序算法则认为排序是稳定的。(但稳定性并非是必须的、最优的)。
时间复杂度、空间复杂度
排序算法的分类
内部排序:数据都在内存中,关注的是什么样的算法可以降低空间复杂度; 外部排序:数据太多,无法全部放入内存,关注的是如何降低读写磁盘的次数
以下讨论的都属于内部排序
1. 插入排序(Insertion Sort)
i从第二个元素开始遍历,如果比前一个元素小,就交换它们的位置,直到到达这个元素应有的位置,i继续遍历下一个元素;使用辅助数temp作为交换辅助。
1
2
3
4
5
6
7
8
9
10
11
12void Sort_Insert(vector<int> &sqlist){
int temp;
for(int i=1;i<sqlist.size();i++){ //遍历每个数据
for(int j=i;j>0;j--){ //比较当前数据和前面的每个数据
if(sqlist[j]<sqlist[j-1]){ //当前数据小就进行交换,temp是辅助变量
temp=sqlist[j-1];
sqlist[j-1]=sqlist[j];
sqlist[j]=temp;
}
}
}
}
空间复杂度:无论多长的数列,每次插入排序只涉及使用temp辅助排序,空间复杂度是常数级,即O(1);
时间复杂度:最简单的情况是序列本来就是有序的,只需要比较不需要移动,时间复杂度是O(n);最坏情况是序列本身是逆序的,时间复杂度是
稳定性:由于条件涉及是小于前一位元素才发生交换,因此相等元素的前后顺序仍保持不变,因此算法是稳定的。
综上所述,插入排序比较适用于小批量的数据,处理大批量数据时间复杂度比较大。
优化方案:
折半查找的插入排序:决定插入位置时不使用j--的方式逐位比较,而是使用折半查找方式查找插入的元素位置,这样优化了查找效率,但是插入效率仍然是一样的,平均时间复杂度仍然是
链表结构的插入排序:基于链表的结构可以实现插入排序,但是不能使用折半查找,链表的插入通过改变指针进行,优化了插入效率,但是比较的复杂度仍是一样的,综合而言时间复杂度仍然是
2. 希尔排序(Shell Sort)
希尔排序的思想是从部分有序到整体有序,首先将序列划分成子表,一般取初始时取增量d=size/2,增量的意思是隔多少位取值,例如有序列6,5,4,3,2,1,size=6,d=3,也即分出6,3、5,2、4,1三个子表,在子表中执行插入排序,该例中子表均为逆序,子表两个位置对换,产生子表3,6、2,5、1,4,合成表后就是3,2,1,6,5,4,此时增量除以2,d=1,代表在该序列不抽值而是直接进行插入排序,即得到1,2,3,4,5,6。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17void Sort_Shell(vector<int> &sqlist){
int n=sqlist.size();
int temp;
//初始增量取size的一半,就是子表只有两个元素,有size/2个子表,循环一次说明间隔n/2的子表排序完毕,直到d=1(代表的子表就是原来的大小)
for(int d=n/2;d>=1;d/=2){
//i和j的结合是子列的插入排序,i和j结合起来看,i负责遍历d开始后面的元素,j负责比较i元素以及i-d元素大小,小于则交换,继续比较i-d和i-2d大小,直到i-d已经小于0了(不包括)。
for(int i=d;i<n;i++){
for(int j=i;j>=d;j-=d){
if(sqlist[j]<sqlist[j-d]){
temp=sqlist[j-d];
sqlist[j-d]=sqlist[j];
sqlist[j]=temp;
}
}
}
}
}
空间复杂度:只使用了辅助变量temp,空间复杂度仍是O(1)
时间复杂度:难以定量分析,最坏情况就是完全逆序时仍然退化成了插入排序,时间复杂度为
稳定性:划分子表策略不同,两个相同元素的相对位置是可能发生改变的,因此希尔排序不具备稳定性。
综上所述,希尔排序适用于中小量的数据,它的时间复杂度略优于插入排序。而且希尔排序是基于划分子数组进行插入排序的思想,要求结构具有顺序存储、随机访问的特性,不适用于链表结构。
3. 冒泡排序(Bubble Sort)
冒泡排序是比较相邻两位元素,如果是前面的元素大,就发生元素交换,例如数列{5,1,6,3,2,4},开始时比较1,5,交换变成{1,5,6,3,2,4},比较5,6,顺序不变,比较6,3顺序改变,变成{1,5,3,6,2,4},接着比较6,2,然后比较6,5,经过第一轮i循环,6就变到了末尾成为最大元素,因此下一次的j取值需要减去1,下一轮需要-2,在下一轮需要-3,因为每一轮都会把前面的大元素放到末尾,也即每一轮j都要减去i。
1 | void Sort_Bubble(vector<int> &sqlist){ |
总而言之,冒泡排序的第一个i循环是把整个列表最大的元素放在末尾,因为不够大的元素会自动停在大元素前面而不发生交换,因此形象地称为冒泡排序。当然,如果j循环采取写法是(int j=n-2;j>=i;j--),则是每次i循环首先把小元素冒泡到数组头部。这种写法和插入排序有些类似,却不是完全相同:插入排序中是从第二个元素开始,逐个和前面元素比较,找到插入的位置,再遍历下一个元素,每次的结果就是把当前元素放到前面的有序序列中。
而采取了(int j=n-2;j>=i;j--)写法的冒泡排序效果确实是让小元素往前冒泡了,但是注意是从j是从末尾开始执行的,例如数列{5,1,6,3,2,4},第一次i循环冒泡排序的结果是{1,5,2,6,3,4};而如果使用插入排序则是{1,5,6,3,2,4},虽然都把1往前带了,但是由于冒泡排序是从结尾开始的,首先是把2往前带了,遇到1才停下,再把1往前带。换言之,如果后面没有了小元素,如{5,1,2,3,4,6},那么两种排序算法流程是一致的。
空间复杂度:O(1)
时间复杂度:和插入排序类似,最好是有序的时候,为O(n),最差是完全逆序时,为
稳定性:因为是相邻的数进行比较,只有大于才发生交换,因此算法是稳定的。
综上所述,冒泡排序的时间复杂度和插入排序类似,前提是引入标志位避免不必要的比较,同时也适用于链表结构。
冒泡排序和插入排序
因为都是前后元素的比较,刚刚接触很容易混淆这两种排序,而事实上它们的原理也是十分雷同,一个明显的差异是:
- 每轮冒泡排序都能确认一个最大元素(或者最小元素),即冒泡出去一个元素,然后再在子表进行排序;插入排序则不然,它会将当前元素排列到适宜的位置,但是在后面的遍历可能出现更小的元素,需要继续前移,导致前面排序的位置也是变化的,因此它是反复折腾已经排好序的子表,直到遍历完全部元素。
4. 快速排序(Quick Sort)
快速排序是实现是基于双指针的,首先定义基准元素pivot(也称枢轴元素,一般取序列的第一个元素或者其中的随机数),小于基准元素的排在左边,大于的排在右边,具体实现方法是:low指向第一个元素,high指向末尾的元素,开始时第一个元素被赋值为pivot,该位置允许被覆盖,从high开始寻找小于基准元素的值,while循环过滤,直到找到并且赋值给第一个元素位置;这时high指向的位置可以被覆盖,就开始从low位置寻找大于基准元素的数据,赋值给high空间,以此类推,直到结束的一种情况也即low和high都指向了一个空余空间,写入基准元素,实现了第一次分表排序,返回新的表头元素low作为新的基准元素。这就是第一个partition函数完成的功能。
在Sort_Quick函数中,分别在新左右子表中执行同样的操作,直到新的low和high再次重合,放入基准元素,重新划分为左右两个子表,随着递归必然会走到只有一个基准元素的表,low=high,在Sort_Quick函数中不再执行。随着使用子表都递归到这一步,排序完成。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23//分区函数,作用是按照基准元素将乱序表分成两部分,小于基准元素的在左边,大于基准元素在右边,返回新的基准元素
int partition(vector<int> &sqlist,int low,int high){
int pivot=sqlist[low]; //取第一位元素为基准
while(low<high){ //说明没有遍历完毕
while (low<high&&sqlist[high]>=pivot)
high--; //high跳过大于pivot的元素
sqlist[low]=sqlist[high]; //小于的赋值给low
while(low<high&&sqlist[low]<=pivot)//low跳过小于pivot的元素
low++;
sqlist[high]=sqlist[low]; //大于的赋值给high
}//循环结束,low、high是重合的
sqlist[low]=pivot; //重合位置是基准元素,左边全是小于基准元素的,右边全是大于基准元素的
return low; //pivot位置已经是确定,下次只需要对其前后元素再排序即可
}
//快速排序
void Sort_Quick(vector<int> &sqlist,int low,int high){
if(low<high){ //只有这种情况需要排序
int pivot=partition(sqlist,low,high); //获取新基准
Sort_Quick(sqlist,low,pivot-1); //递归左子表
Sort_Quick(sqlist,pivot+1,high);//递归右子表
}
}
快速排序的复杂度很大程度上依赖于递归层数的调用,这种将表一分为二的结构显然是树的结构,第一层基准元素作为根结点,最好的情况是每次挑选的基准元素恰好能把序列分成均匀的两部分,那么递归的层数就是类似完全二叉树的结构,二叉树层数也是递归的层数,数量级是
稳定性:相同元素相对位置可能不同,是不稳定算法。
空间复杂度:在每层递归中,都有自己子表的low、high、pivot,因此复杂度和递归层数是正相关的,即为O(递归层数),最好是
时间复杂度:时间复杂度来自执行划分子表的复杂度,对开始时对n个元素进行划分,遍历n个元素,因此复杂度数量级是O(n),划分子表后,各自对n-1个元素进行再次划分,复杂度不超过O(n),总体而言复杂度是O(递归层数*n),故最优是
综上所述,作为把快速刻入名字的算法,总体而言,快速排序是内部排序性能最优的算法。
5. 选择排序(Selection Sort)
5.1 简单选择排序(直接选择排序)
这是顺序表选择排序的算法,准确而言称为简单选择排序,其思想是使用i遍历每一个元素,j遍历i位置到末尾的每个元素,找出最小元素j_min位置,将j_min与i元素互换,每次循环i位置的元素一定是i到末尾最小的元素,完成了排序。除了简单选择排序,另一种将元素构造成树结构的选择排序,称为堆排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17void Sort_Selection(vector<int> &sqlist){
int n=sqlist.size();
int temp;
for(int i=0;i<n;i++){ //i遍历元素
int j_min=i; //假设最小的j为当前的遍历的元素
for(int j=i+1;j<n;j++){ //遍历i位置之后的每一个元素
if(sqlist[j]<sqlist[j_min]){ //找出i位置到末尾最小的元素
j_min=j; //记录元素位置
}
}
//将首位和最小元素交换
temp=sqlist[i];
sqlist[i]=sqlist[j_min];
sqlist[j_min]=temp;
}
//选择排序:每次循环执行都会把i位置到末尾最小的元素放到前面
}
时间复杂度:无论元素是顺序还是逆序,n个元素都要经过n-1次对比,因此时间复杂度是
稳定性:对比和交换是跨越元素进行的,不一定是相邻元素,因此大小相同的元素前后位置有可能发生交换,是不稳定的算法。
特性:顺序表、链表都可以使用。
5.2 堆排序
堆结构
堆排序是一个比较复杂的算法,它是基于一种数据结构——堆(Heap)实现的,介绍堆排序,主要还是为了引入这种数据结构,它在处理某些问题(优先队列)是一种较优的算法。对于一个数组,对于位置i(1<i<=len/2),如果满足位置i元素恒大于等于2i和2i+1位置,那么这个数组结构就是大根堆(大顶堆),如果恒小于等于,就是一个小根堆(小顶堆),为了直观描述这种特性,通常使用二叉树进行描述,将堆组成二叉树(按层序遍历进行编号):
1. 大根堆就是所有根结点元素大小大于等于左右孩子;
2. 小根堆就是所有根结点元素小于等于左右孩子;
对二叉树而言:按照层序遍历的顺序放置堆元素和编号,对于编号i(1<i<=len/2)的结点,其左孩子的结点是2i,右孩子的结点是2i+1,其父结点编号是i/2;
建立大根堆
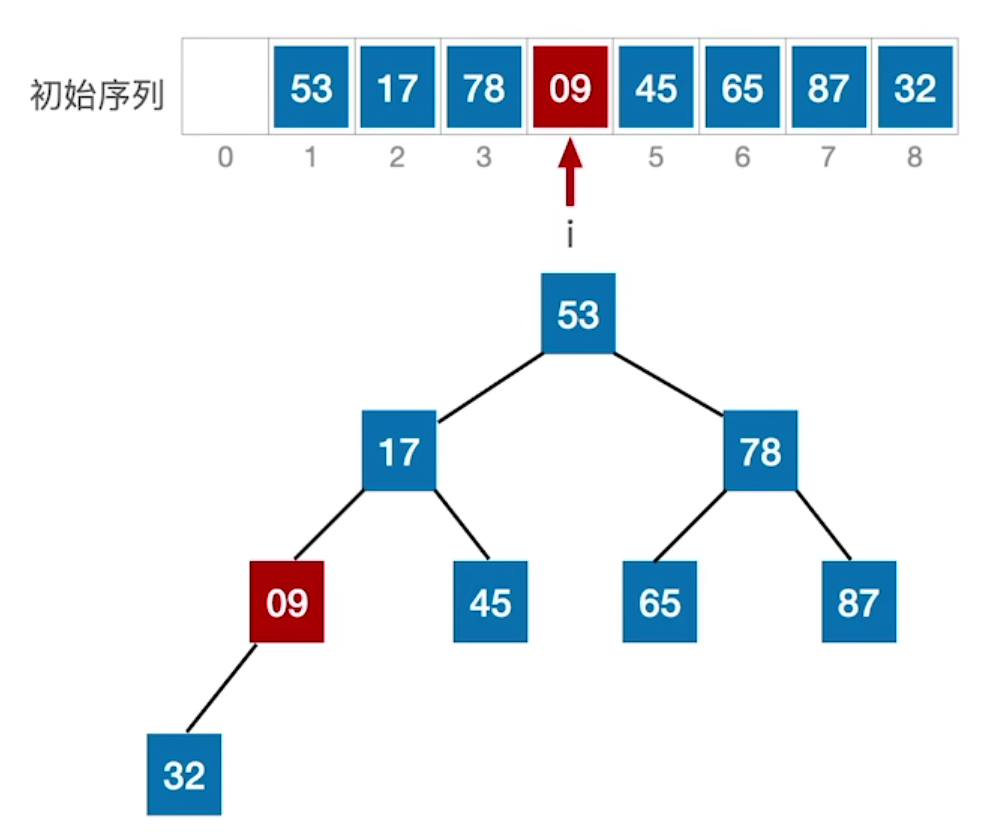 1.
首先需要对最后一个根结点(编号为len/2)进行处理,比较根结点与左右孩子的大小,如果根结点小于左右孩子,则交换根结点与最大孩子的值;
1.
首先需要对最后一个根结点(编号为len/2)进行处理,比较根结点与左右孩子的大小,如果根结点小于左右孩子,则交换根结点与最大孩子的值;
同样的方法处理上一个根结点(09->78->17),直到采取同样的方法处理树的根结点(53);
处理树的根结点时,53如果作为小元素会进一步向左子树或者右子树下滤,因此还需要进一步采取同样的交换方法调整在左子树或者右子树,使其下滤至合适的孩子位置。
最后处理结果: 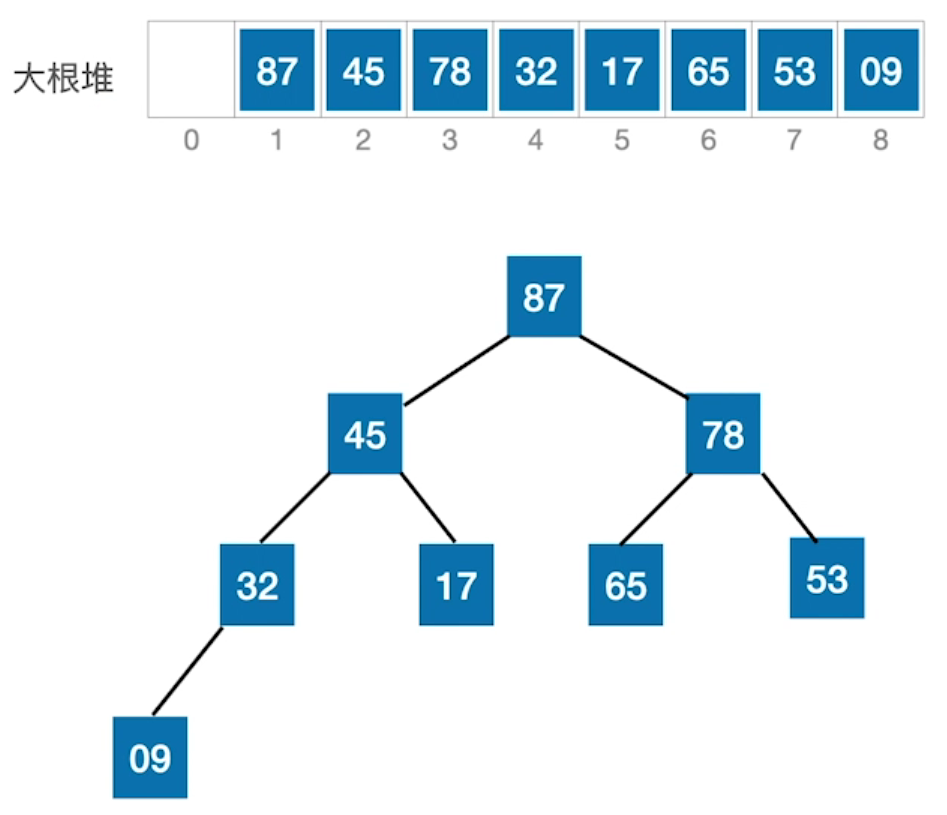
基于大根堆的排序
首先要明确的是,目前讨论的排序是从小到大进行排序,那么为什么要使用大根堆而不是小根堆呢?假设使用的是小根堆,根结点的元素就是整个结构最小的元素,将根结点弹出(这也是一种优先队列结构),末尾结点补上(末尾结点是大元素),因此需要进行元素下滤,使得下一个最小结点重新占据根结点,继续弹出,如此类推;
这种方法的坏处是破坏了树的结构,需要考虑空间释放,而且弹出的元素需要额外的空间进行存储,带来了不必要的空间复杂度。使用大根堆则可以原地进行排序:当大根堆形成时,根结点元素就是最大的元素,与末尾元素交换,然后只需要重新在长度-1的数组上进行大根堆的创建(实际上是将占据根结点的小元素下滤),重新将最大元素放在根结点,长度继续-1创建大根堆,直到最后下标为1的元素与根结点进行交换,整个数组(树结构)就是增序的。
C语言的实现: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
//用于创建大顶堆
void BuildMaxHeap(int num[],int len,int i){
int largest=i; //假设最大元素的下标就是i
int left=2*i+1; //i的左孩子
int right=2*i+2; //i的右孩子
if(left<len&&num[left]>num[largest]) //left<len确保左孩子存在,而不是越数组界
largest=left; //左孩子大,最大元素下标指向左孩子
if(right<len&&num[right]>num[largest]) //右孩子存在
largest=right; //右孩子大指向右孩子
if(largest!=i){ //指向不是i,swap(num[i],num[largest])
int temp=num[i]; //即交换根结点与左孩子和右孩子中较大的一个
num[i]=num[largest];
num[largest]=temp;
BuildMaxHeap(num,len,largest); //发生了下滤,要检查下滤有没有改变子树的大根堆结构,如果有就递归处理使其变回大根堆
}
}
void Heapsort(int num[],int len){
for(int i=len/2-1;i>=0;i--){//从最后一个根结点开始,编号必然是len/2-1,直到对根结点处理
BuildMaxHeap(num,len,i);
} //至此,得到了一棵大顶堆
//开始排序,将最大元素交换到最后一位,重新执行大顶堆构建
for(int i=len-1;i>0;i--){
int temp1=num[0]; //交换根结点和末尾结点位置;
num[0]=num[i];
num[i]=temp1;
BuildMaxHeap(num,i,0); //注意i代表长度,是不断--的,每次执行重新构建大顶堆时,因为刚刚执行完交换,0位置(根结点)始终是需要下滤的元素
}
}
int main(){
int num[] = {53, 17, 78, 9, 45, 65, 87, 32};
int len=sizeof(num)/sizeof(int);
Heapsort(num,len);
for(int i=0;i<len;i++){ //增序排列
printf("%d\t",num[i]);
}
}
小顶堆的降排序
从大到小排序的C++实现:小顶堆+下滤 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
using namespace std;
//建立小顶堆
void BuildMinHeap(vector<int>&nums,int len,int i){
int smallest =i; //假设根结点为指向最小元素的下标
int left=2*i+1; //根结点的左孩子
int right=2*i+2; //右孩子
if(left<len && nums[left]<nums[smallest]) //left<n代表树左孩子存在
smallest=left;
if(right<len && nums[right]<nums[smallest])
smallest=right;
if(smallest!=i){
swap(nums[smallest],nums[i]); //对换根结点与孩子中较小的一个
BuildMinHeap(nums,len,smallest); //对换后smallest指向的是原来的根结点,原来的根结点变成了孩子位置,因此要递归其子树,该结点有可能需要进一步下滤
}
}
void Heapsort(vector<int>&nums,int len){
for(int i=len/2-1;i>=0;i--){ //从最后一个根结点开始构建小顶堆
BuildMinHeap(nums,len,i);
}
for(int i=len-1;i>0;i--){ //不断把最小的元素放在后面
swap(nums[0],nums[i]);
BuildMinHeap(nums,i,0);
}
}
int main(){
vector<int>nums={53, 17, 78, 9, 45, 65, 87, 32};
int len=nums.size();
Heapsort(nums,len);
for(const auto&pos:nums){
cout<<pos<<'\t'; //输出大小是减序
}
return 0;
}
6. 归并排序(Merge Sort)
归并排序的思想是来源于合并两个本来就有序的数组,这很容易实现,只需要使用i、j分别指向这两个数组,比较i、j对应的元素,小的插入到新数组中即可完成合并。而无序的数组开始时可以认为相邻的元素就是需要合并的数组,如图所示:
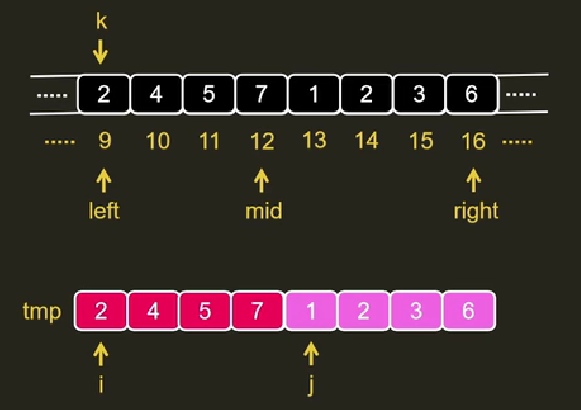 分别比较i、j,将较小值写入k,如果i耗尽了(到达mid),就直接复制j到k位置;如果j耗尽了(到达high),就复制i到k位置;
分别比较i、j,将较小值写入k,如果i耗尽了(到达mid),就直接复制j到k位置;如果j耗尽了(到达high),就复制i到k位置;
这是建立在归并“两个有序的数组”逻辑,对于完全无序的数组,需要使用两层递归将数组化成二叉树,如下图(由下而上),然后对相邻元素执行多次归并操作(由上而下),就完成了归并排序。
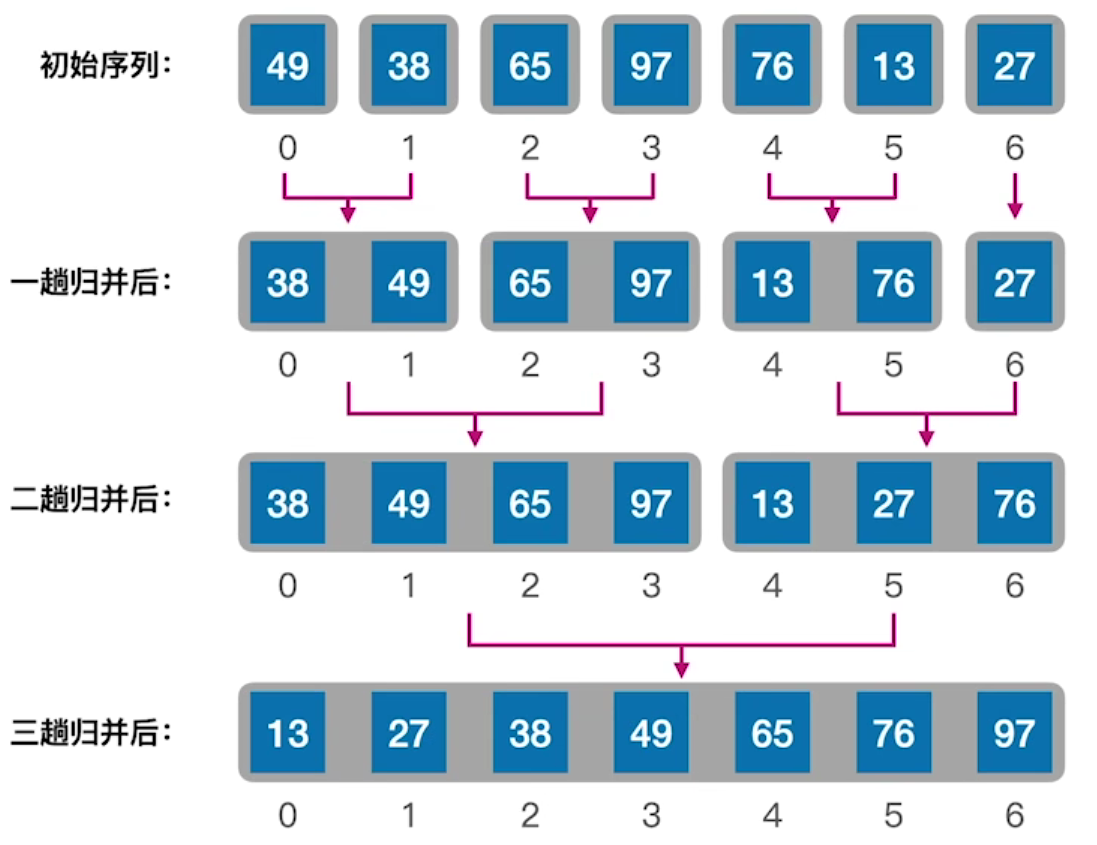
以下: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26//二路有序数组的归并,归并low——mid,和mid+1——high
void Sort_Two(vector<int>&nums,int low,int mid,int high){
vector<int>temp = nums; //复制数组副本
int i,j,k;
for(i=low,j=mid+1,k=i; i<=mid&&j<=high; k++){
if(temp[i]<=temp[j]) //i是前半子表,i位置小,复制i
nums[k] = temp[i++];
else //j是后半子表,j小复制j
nums[k] = temp[j++];
}
//其中一方元素排序完成,复制剩下元素
while(i<=mid) //i剩余,直接复制i
nums[k++] = temp[i++];
while(j<=high)
nums[k++] = temp[j++];
}
//分割+逐路归并
void Sort_Merge(vector<int>&nums,int low,int high){
if(low<high){ //low==high就说明已经分割到单个元素了
int mid = (low+high)/2;
Sort_Merge(nums,low,mid); //分割,最后分割到左表的叶子结点
Sort_Merge(nums,mid+1,high); //最后分割到右表的叶子结点
Sort_Two(nums,low,mid,high); //排序
}
}
时间复杂度:从图片看,本算法采取了二路归并的算法(也就是最底层的递归只有两个元素进行归并),因此这种结构类似一棵倒立的二叉树,称为“归并树”。递归的层数是
空间复杂度:归并排序的空间复杂度来自两个部分,一个是辅助数组sqlist1,它的大小和输入数组大小是一致的,产生O(n)的空间复杂度,其次,递归调用中递归栈(层数)是
稳定性:我们的处理方法是sqlist1[i]<=sqlist1[j]会把前面的放到新数组,因此前面元素的优先级是高于后面的,相对位置不会改变,所以算法是稳定的。
总结
排序算法通常关注时间复杂度、空间复杂度、稳定性三种指标,其中插入、冒泡、归并排序均属于稳定算法,希尔、快速、直接选择、堆排序均属于不稳定算法;时空复杂度只针对平均情况,具体性能要具体分析,例如小批量的数据排序可能冒泡排序性能较优,对于大批量数据快速、归并、堆排序都具有O(nlogn)的平均复杂度,归并和堆排序的复杂度都是稳定的,而快速排序在逆序、顺序(斜树)时会带来

